如今机器学习、深度学习可谓炙手可热，人工智能也确实开始影响、改变着我们的生活。正因如此，很多同学开始接触或者学习这方面的知识。机器学习的入门是有难度的，因为它不仅要求你会编码，还要你熟悉高等数学，比如线性代数，微积分等，除此之外，还要懂统计学。如果你想入门机器学习，那么一定要好好学习逻辑回归。原因如下：

1.逻辑回归可以帮你更好地理解机器学习；

2.逻辑回归已经可以解决多数问题了；

3.逻辑回归是统计学习的重要工具；

4.逻辑回归是神经网络的基础；

下面开始我们的正文，在正式介绍逻辑回归前，我们先从逻辑回归的基础--线性回归开始。

1.线性回归

现在有如下图所示的数据集 $D = \left \{ (x_{1},y_{1}),(x_{2},y_{2}),\cdots ,(x_{m},y_{m}) \right \}$ 。线性回归（Linear Regression）试图学习得一个线性模型尽可能准确地预测每一个x所对应真实值y的输出标记。

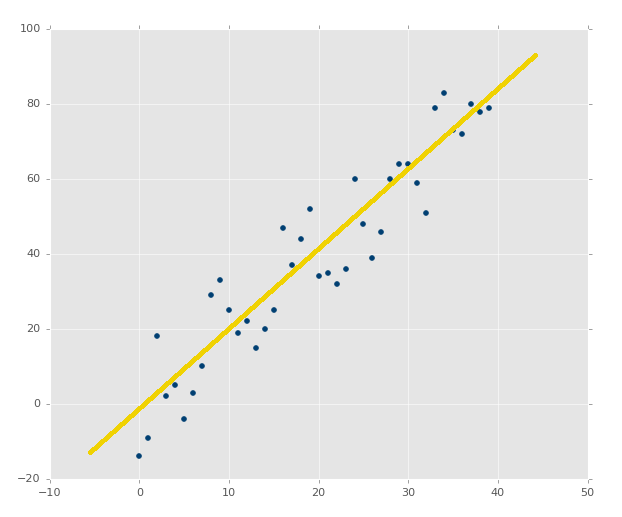
machine learning tutorials

上图中的黄色直线就是我们想要学习得到的模型，也叫假设函数（Hypothetical function）：

$h(x_{i})=wx_{i}+b$ ，使得 $h(x_{i}) \simeq y_{i}$ (1)

有了假设函数，就可以得到损失函数，它是用来估量你模型的预测值f(x)与真实值y的不一致程度，即误差。

我们只要确定好模型中的w和b，即可确定模型。如何确定w和b呢，这里就要引入均方误差的概念，采用均方差作为损失函数。

均方误差，也叫最小二乘法，是指真实值y和预测值f(x)之间的方差平均值，它是回归问题中最常用的性能度量，我们将用最小二乘法作为损失函数：

$J = \frac{1}{m}\sum_{i=1}^{m}(h(x_{i})-y_{i})^{2}$ (2)

我们要让式（2）均方误差最小化，即

$(w^{*},b^{*}) = \arg min_{w,b}\sum_{i=1}^{m}(h(x_{i})-y_{i})^{2}$

$=\arg min_{w,b}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$ (3)

这样，问题就转为求解w和b使得式（2）的变式：

$J_{(w,b))}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$ （4）

最小化的过程。这个过程也叫线性回归模型的最小二乘“参数估计”。

式（4）是关于w和b的凸函数，当它关于w和b的导数均为0时，得到w和b的最优解。这是偏导数的特性，大家应该都知道。

我们将式（4）分别对w和b求导，得到：

$\frac{\partial E_{(w,b)}}{\partial w} = 2\left (\sum_{i=1}^{m}x^{2}_{i} -\sum_{i=1}^{m}(y_{i}-b)x_{i}\right )$ (5)

$\frac{\partial E_{(w,b)}}{\partial b} = 2\left (mb -\sum_{i=1}^{m}(y_{i}-wx_{i})\right )$ (6)

令式（5）和式（6）为零，即可得到：

$w= \frac{\sum_{i=1}^{m}y_{i}(x_{i}-\bar{x})}{\sum_{i=1}^{m}x^{2}_{i}-\frac{1}{m}\left ( \sum_{i=1}^{m}x_{i} \right )^{2}}$ (7)

$b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i})$ (8)

式（7）中 $\bar{x}$ 为x所有取值的均值。

更一般的，我们将x的每一个取值向量化，即：

$x_{i} = (x_{i1},x_{i2},\cdots ,x_{in})$

则，线性回归模型可以写为：

$\bg_white h(x_{i})=w^{T}x_{i}+b$ (9)

2.联系函数

真实环境下，线性模型是很难适用的，或者说，适用的场景很少。比如，y的取值是在指数尺度上的映射，它的函数关系为：

$y = e^{w^{T}x+b}$ （10）

对于这样的模型我们如何使用线性模型的思想去建模呢？这就需要在原来的线性模型的基础上，做些函数映射即可。我们先将

式（10）两边做些等价变化，得到下式：

$\ln y = w^{T}x+b$ （11）

这样一来，在形式上是不是跟线性模型就很像了，我们看到等式右边就是我们上面提到的线性模型，仍可做线性回归。但实质上我们已经是在对输入x到输出y的非线性函数建模了。

所以，对于非线性模型，我们只要稍作映射就可以继续采用线性回归的思维去求解。更一般地，对于非线性模型，令

$y = g^{-1}(w^{T}x+b)$ (12)

这样就得到了广义的线性模型。式（12）中的 $g^{-1}$ 就是“联系函数”。对于式（10），它的的 g 函数就是 $\ln$ 函数。

这就是为什么我们要先介绍线性模型的原因，因为下面的逻辑回归也是基于线性回归的思想。这就是数学之美！

3.sigmoid函数

要说逻辑回归，必须先说下它的核心，sigmoid函数。

我们知道，线性回归模型是针对回归问题的，逻辑回归虽然它的名字里有“回归”二字，但它却是一个用于解决分类问题的算法。

这里我们考虑二分类问题。对于二分类问题，它的输出 y 取值只有 0 和 1 两种。 $y\in \left \{ 0,1 \right \}$ 。这样通过上面一节联系函数的介绍，大家应该知道，我们需要找到一个联系函数 g ，将线性回归模型的预测值，转为 0 或者 1。最理想的函数是“单位阶跃函数”，也称做赫维赛德（Heaviside）函数。函数图形如下：

但由于它不是连续函数，所以无法用作 g 函数。有没有图形类似上图，且单调可微的函数替代它呢？答案就是我们这节的主角，sigmoid函数，也叫对数几率函数（logistic function）。

Sigmoid函数的表达式为：

$y = \frac{1}{1+e^{-z}}$ (13)

它的函数图形为：

将sigmoid函数作为 g 函数带入到式（12）中，得到：

$y = \frac{1}{1+e^{-(w^{T}x+b)}}$ (14)

这样我们就可以看出，我们依旧是用线性回归模型去逼近真实的对数几率函数模型。类似于式（11），我们将式（14）做些变化，得到：

$\ln \frac{y}{1-y} = w^{T}x+b$ （15）

如果我们把 y 看做是 x 为 1 的可能性，那么1 - y 就是 x 为 0 的可能性。这两者的比值就是“几率”。反应了 x 为 1 的相对可能性。对它们的比值取对数，就得到“对数几率”（log odds,也叫logit），这就是逻辑回归命名的由来。其实它跟逻辑两个字根本不搭嘎（手动滑稽）。

所以逻辑回归的本质是概率。它可以得到y的预测值为0和1的概率，在sklearn中，通过逻辑回归建模，使用 predict_proba 方法可以看到0，1对应的概率。使用 predict 方法则以0.5为分界线，直接告诉你x对应的预测结果0还是1。

4.损失函数

在计算逻辑回归的损失函数之前，我们先做些准备工作。

我们先将线性部分的公式 $w^{T}x+b$ 简化为 $\theta ^{T}x$ ，如果你不知道为什么能这么写，那就该补补线性代数的功课了。这样一来我们的假设函数，就可以写成：

$h_{\theta }(x) = \frac{1}{1+e^{-\theta ^{T}x}}$ （16）

我们令：

$z = \theta ^{T}x$ (17)

$g(z) = \frac{1}{1+e^{-z}}$ (18)

则，我们的假设函数式（16）可写成：

$h_{\theta }(x) = g(\theta ^{T}x)$ (19)

这样，我们按照第一节使用最小二乘的方式得到公式（20）：

$J(\theta ) =\frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x_{i}) - y_{i})^{2}$ （20）

我们知道求解最优解是通过求导的方式。但由于在逻辑回归中，假设函数的形式如式（16）所示，它无法使用线性模型的这种方式求最优解。为什么线性模型可以，逻辑回归就不行了呢。因为线性回归的最小二乘方程是个凸函数，而逻辑回归的不是。他两的图形如下，左图为逻辑回归，右图为线性回归：

既然使用传统的最小二乘发无法求出最优解，我们就需要换种方法，重新写个损失函数。

我们使用“极大似然法”来求最优解。使用极大似然法得到新的损失函数为：

$cost(h_{\theta }(x),y)= \right.-log(h_{\theta }(x)),y=1$ (21)

$cost(h_{\theta }(x),y)= \right.-log(1 -h_{\theta }(x)),y=0$ (22)

将式(21)(22)两者合为一个完整的损失函数式（23）：

$cost(h_{\theta }(x),y)= -ylog(h_{\theta }(x)) - (1-y)log(1-h_{\theta }(x))$ (23)

更一般的，针对所有训练样本，我们的损失函数为：

$J(\theta )= \frac{1}{m}\sum_{i=1}^{m}cost(h_{\theta }(x_{i}),y_{i})$

$J(\theta)= -\frac{1}{m}\left [ \sum_{i=1}^{m}y_{i}log(h_{\theta }(x_{i})) + (1-y_{i})log(1-h_{\theta }(x_{i}))\right ]$ (24)

有了损失函数，我们只要能找到 $\theta$ ，让损失函数最小，就可以得到我们的假设函数 $h_{\theta }(x)$ ，也就得到最终的逻辑回归模型。

通过不断的更新 $\theta$ 的值，让损失函数不断变小，直至最小的过程是一种最优化的过程。求解最优化问题的方法一般采用梯度下降法。

5.梯度下降法

梯度下降方法基于以下的观察：如果实值函数 $f(x)$ 在点 a 处可微且有定义，那么函数 $f(x)$ 在 a 点沿着梯度相反的方向 $-\bigtriangledown f(a)$ 下降最快。

因而，如果 $\bg_white b=a - \eta \bigtriangledown f(a)$ ，对于 $\bg_white \eta > 0$ 为一个够小数值时成立，那么 $\bg_white f(b) \leq f(a)$ 。

考虑到这一点，我们可以从函数 $f(x)$ 的局部极小值的初始估计 $x_{0}$ 出发，并考虑如下序列 $x_{0},x_{1},x_{2}...x_{m}$ 使得

$x_{n+1}=x_{n} - \eta \bigtriangledown f(x_{n})$ ，因此可得到 $f(x_{m}) \leq ...\leq f(x_{1})\leq f(x_{0})$ 。

如果顺利的话序列 $\left ( x_{m} \right )$ 收敛到期望的极值。

下面的图片示例了这一过程，这里假设 $f(x)$ 定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数 $f(x)$ 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数 $f(x)$ 值最小的点。

6.梯度公式推导

通过第五节的介绍，我们知道要想让损失函数找到最小值，只要求出损失函数，即式（24）的关于 $\theta$ 的偏导数（也就是梯度），然后通过梯度，不断更新 $\theta$ 值，从而得到最优解（也就是损失函数的极小值点）。

按照第五节的介绍，我们写出 $\theta$ 的更新表达式为：

$\large \theta_{n+1} = \theta _{n} - \eta \bigtriangledown J\left ( \theta \right )$

也就是：

$\large \theta_{j+1} = \theta _{j} - \eta \frac{\partial }{\partial \theta _{j}}J\left ( \theta \right )$ （25）

所以，到这里，我们的工作就是对损失函数式（24）求关于 $\theta$ 偏导数。

这是全部理论知识当中的难点也是烦点，有基础的同学可以自行推导。下面是公式推导过程：

首先记下这几个公式，第一个是损失函数，式（24），也就是我们要求导的对象：

$J(\theta)= -\frac{1}{m}\left [ \sum_{i=1}^{m}y_{i}log(h_{\theta }(x_{i})) + (1-y_{i})log(1-h_{\theta }(x_{i}))\right ]$

然后是假设函数，式（16）：

$h_{\theta }(x_{i}) = \frac{1}{1+e^{-\theta ^{T}x_{i}}}$

我们令 $z = \theta ^{T}x$ ，则式（16）可以写成下式：

$h_{\theta }(x) = \frac{1}{1+e^{-z}} = \frac{e^{z}}{1+e^{z}}$ (26)

然后，为了让数学公式看着不那么吓人，不那么复杂，我们将式（24）中的所有下标省掉，将前面的系数 -1/m 先省略，从而简写成式（27）的形式：

$J(\theta)= ylog(h_{\theta }(x)) + (1-y)log(1-h_{\theta }(x))$ (27)

将其展开：

$J(\theta)= ylog(h_{\theta }(x)) - ylog(1-h_{\theta }(x)) + log(1-h_{\theta }(x))$

将前两项合并：

$J(\theta)= ylog(\frac{h_{\theta }(x)}{1-h_{\theta }(x)}) + log(1-h_{\theta }(x))$

按照式（26），将 $h_{\theta }(x)$ 替换，得到：

$J(\theta)= ylog(\frac{ \frac{e^{z}}{1+e^{z}} }{ 1-\frac{e^{z}}{1+e^{z}} }) + log(1-\frac{e^{z}}{1+e^{z}})$

对于等式右边的第一部分 log 函数里的分子分母分别乘以 $1+e^{z}$ ，等式右边展开，得到

$J(\theta)= ylog(\frac{e^{z}}{1+e^{z}-e^{z}}) + log(\frac{1+e^{z}-e^{z}}{1+e^{z}})$

进一步化简：

$J(\theta)= ylog(e^{z}) + log(\frac{1}{1+e^{z}})$

继续化简，注意中间的 '＋' 号变为了 '-' 号，得到最终简化的损失函数公式（28）：

$J(\theta)= yz- log(1+e^{z})$ （28）

对式（28）求导，得到求导式(29)：

$\frac{\partial J}{\partial \theta }= y\frac{\partial z}{\partial \theta }- \left [ log(1+e^{z}) \right ]{}'$ (29)

在对简化后的损失函数求导之前，先复习下梯度优化的精髓，链式法则。

链式法则或链锁定则（英语：chain rule），是求复合函数导数的一个法则。设 f 和 g 为两个关于 x 的可导函数，则复合函数 $(f\circ g)(x)$ 的导数 $(f\circ g)'(x)$ 为：

$(f\circ g)'(x)=f'(g(x))g'(x).$

所以式（28）等式右边的log函数的关于θ的导数为：

$log(1+e^{z}){}' = \frac{1}{1+e^{z}}\cdot (1+e^{z}){}'\cdot \frac{\partial z}{\partial \theta }$

进一步求导，得到：

$log(1+e^{z}){}' = \frac{1}{1+e^{z}}\cdot e^{z}\cdot \frac{\partial z}{\partial \theta }$

最后得到式（29）：

$log(1+e^{z}){}' = \frac{e^{z}}{1+e^{z}}\frac{\partial z}{\partial \theta }$ （30）

将式（30）代入式（29），得到：

$\frac{\partial J}{\partial \theta }= y\frac{\partial z}{\partial \theta }- \frac{e^{z}}{1+e^{z}}\frac{\partial z}{\partial \theta }$

进一步化简，得到：

$\frac{\partial J}{\partial \theta }= (y- \frac{e^{z}}{1+e^{z}})\frac{\partial z}{\partial \theta }$

由式（26），可进一步得到：

$\frac{\partial J}{\partial \theta }= (y- h_{\theta }(x))\frac{\partial z}{\partial \theta }$ (31)

由 $z = \theta ^{T}x$ ，得到最后的导数为：

$\frac{\partial J}{\partial \theta }= (y- h_{\theta }(x))x$

由于开始我们为了方便，去掉了系数和小标，现在，将他们加上，得到最终的损失函数导数式（32）：

$\frac{\partial J}{\partial \theta }= \frac{1}{m} \sum_{i=1}^{m} (h_{\theta }(x^{i}) - y^{i})x^{i}$ (32)

得到导数后，我们将它代入 θ 的更新表达式（25）中，从而得到最终的结果：

$\large \theta_{j+1} = \theta _{j} - \frac{\eta }{m} \sum_{i=1}^{m} (h_{\theta }(x^{i}) - y^{i})x^{i}_{j}$ (33)

有了式（33），下面我们就可以通过代码实现逻辑回归了，至此全文结束。

本文参考资料：

1.周志华，《机器学习》

2.吴恩达coursera教程，https://www.coursera.org/learn/machine-learning/home/welcome

3.维基百科

机器学习：逻辑回归详细推导