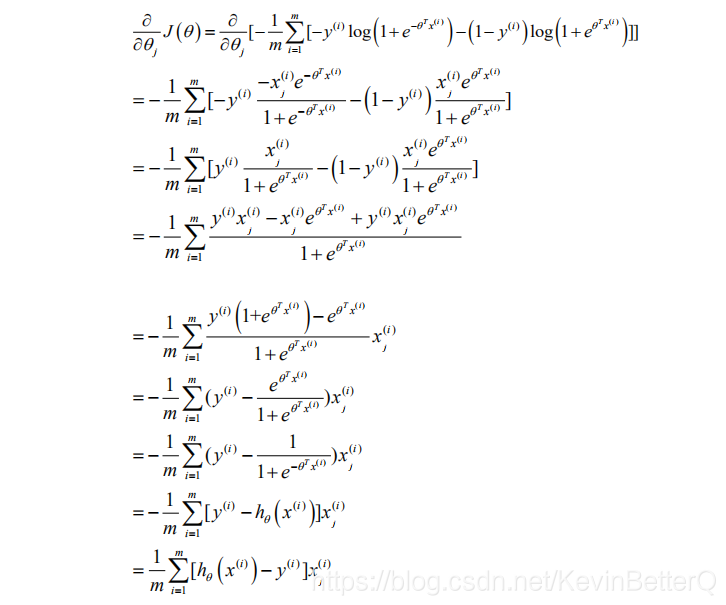版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/KevinBetterQ/article/details/83472878
线性模型可以进行回归学习(参见【机器学习模型1】- 线性回归 ),但如何用于分类任务?需要找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。
y
y
y
{
0
,
1
}
\{0, 1\}
{ 0 , 1 }
z
=
w
T
x
+
b
z = w^Tx+b
z = w T x + b
R
R
R
z
z
z
0
/
1
0/1
0 / 1
S
i
g
m
o
i
d
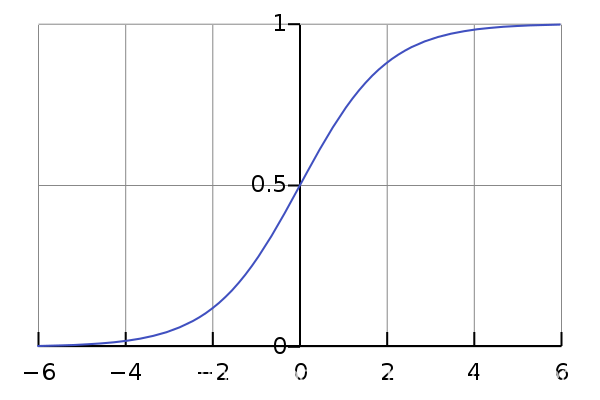
Sigmoid
S i g m o i d
y
=
1
1
+
e
−
z
y=\frac{1}{1+e^{-z}}
y = 1 + e − z 1
z
z
z
y
y
y
根据广义线性模型
y
=
g
−
1
(
θ
T
x
)
y=g^{-1}(\theta^T x)
y = g − 1 ( θ T x )
g
−
1
(
)
g^{-1}()
g − 1 ( )
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}
h θ ( x ) = 1 + e − θ T x 1
对数几率函数:逻辑回归也称为对数几率函数。
h
θ
(
x
)
h_\theta(x)
h θ ( x )
1
−
h
θ
(
x
)
1-h_\theta(x)
1 − h θ ( x ) 所以
h
θ
(
x
)
1
−
h
θ
(
x
)
\frac{h_\theta(x)}{1-h_\theta(x)}
1 − h θ ( x ) h θ ( x )
h
θ
(
x
)
1
−
h
θ
(
x
)
>
1
\frac{h_\theta(x)}{1-h_\theta(x)} > 1
1 − h θ ( x ) h θ ( x ) > 1 “几率” 。
l
n
h
θ
(
x
)
1
−
h
θ
(
x
)
ln\frac{h_\theta(x)}{1-h_\theta(x)}
l n 1 − h θ ( x ) h θ ( x ) “对数几率”
所以,逻辑回归实际上是用线性回归模型的预测来逼近真实的对数几率。
1) 代价函数公式:
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
n
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
n
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}[ y^{(i)}lnh_\theta(x^{(i)})+(1-y^{(i)})ln(1-h_\theta(x^{(i)})) ]
J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) l n h θ ( x ( i ) ) + ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ] 极大似然法 :根据给定数据集,最大化对数似然函数:
L
(
θ
)
=
∑
i
=
1
m
l
n
P
(
y
(
i
)
∣
x
;
θ
)
L(\theta) = \sum_{i=1}^{m}lnP(y^{(i)}|x;\theta)
L ( θ ) = i = 1 ∑ m l n P ( y ( i ) ∣ x ; θ )
P
(
y
=
0
∣
x
;
θ
)
=
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
P
(
y
=
1
∣
x
;
θ
)
=
1
−
h
θ
(
x
)
=
e
−
θ
T
x
1
+
e
−
θ
T
x
=
1
e
θ
T
x
+
1
P(y=0|x;\theta) = h_\theta(x)=\frac{1}{1+e^{-\theta^T x}}\\ P(y=1|x;\theta) = 1-h_\theta(x)=\frac{e^{-\theta^T x}}{1+e^{-\theta^T x}} = \frac{1}{e^{\theta^T x}+1} \\
P ( y = 0 ∣ x ; θ ) = h θ ( x ) = 1 + e − θ T x 1 P ( y = 1 ∣ x ; θ ) = 1 − h θ ( x ) = 1 + e − θ T x e − θ T x = e θ T x + 1 1
P
(
y
∣
x
;
θ
)
=
(
h
θ
(
x
)
)
y
(
1
−
h
θ
(
x
)
)
(
1
−
y
)
P(y|x;\theta) = (h_\theta(x))^y(1-h_\theta(x))^{(1-y)}
P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) ( 1 − y )
L
(
θ
)
=
∑
i
=
1
m
[
y
(
i
)
l
n
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
n
(
1
−
h
θ
(
x
(
i
)
)
)
]
L(\theta) =\sum_{i=1}^{m}[ y^{(i)}lnh_\theta(x^{(i)})+(1-y^{(i)})ln(1-h_\theta(x^{(i)})) ]
L ( θ ) = i = 1 ∑ m [ y ( i ) l n h θ ( x ( i ) ) + ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ]
L
(
θ
)
L(\theta)
L ( θ )
J
(
θ
)
=
−
1
m
L
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
n
h
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
l
n
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(\theta) = -\frac{1}{m}L(\theta) = -\frac{1}{m}\sum_{i=1}^{m}[ y^{(i)}lnh_\theta(x^{(i)})+(1-y^{(i)})ln(1-h_\theta(x^{(i)})) ]
J ( θ ) = − m 1 L ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) l n h θ ( x ( i ) ) + ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ]
为什么除以m?在使用样本不同数量的多个批次来更新
θ
\theta
θ
1)参数更新方程:
θ
j
=
θ
j
−
α
1
m
∑
i
=
1
m
[
h
θ
(
x
(
i
)
)
−
y
(
i
)
]
x
j
(
i
)
\theta_j = \theta_j - \alpha\frac{1}{m}\sum_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]x_j^{(i)}
θ j = θ j − α m 1 i = 1 ∑ m [ h θ ( x ( i ) ) − y ( i ) ] x j ( i )
2)推导过程:
设定:初始值
θ
\theta
θ
α
\alpha
α
不断更新
θ
\theta
θ
θ
j
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
\theta_j = \theta_j -\alpha\frac{\partial }{\partial \theta_j} J(\theta)
θ j = θ j − α ∂ θ j ∂ J ( θ ) (Ref:参考吴恩达Cousera机器学习课程 6.4节)
直到
梯
度
Δ
θ
=
∂
∂
θ
j
J
(
θ
)
<
阈
值
ε
梯度\Delta\theta = \frac{\partial }{\partial \theta_j} J(\theta) < 阈值\varepsilon
梯 度 Δ θ = ∂ θ j ∂ J ( θ ) < 阈 值 ε
θ
\theta
θ
3)向量化表示
θ
=
θ
−
α
m
X
T
(
1
1
+
e
−
X
θ
−
y
)
\theta = \theta - \frac{\alpha}{m}X^T(\frac{1}{1+e^{-X\theta}}-y)
θ = θ − m α X T ( 1 + e − X θ 1 − y )
X,y表示如下:
X
=
[
X
1
(
1
)
X
2
(
1
)
.
.
.
X
n
(
1
)
X
1
(
2
)
X
2
(
2
)
.
.
.
X
n
(
2
)
.
.
.
.
.
.
.
.
.
.
.
.
X
1
(
m
)
X
2
(
m
)
.
.
.
X
n
(
m
)
]
,
θ
=
[
θ
1
θ
2
.
.
.
θ
n
]
,
y
=
[
y
1
y
2
.
.
.
y
m
]
,
X=\begin{bmatrix} X^{(1)}_1& X^{(1)}_2& ...& X^{(1)}_n& \\ X^{(2)}_1& X^{(2)}_2& ...& X^{(2)}_n& \\ ...& ...& ...& ...& \\ X^{(m)}_1& X^{(m)}_2& ...& X^{(m)}_n& \\ \end{bmatrix}, \theta=\begin{bmatrix} \theta_1& \\ \theta_2& \\ ...& \\ \theta_n& \\ \end{bmatrix}, y=\begin{bmatrix} y_1& \\ y_2& \\ ...& \\ y_m& \\ \end{bmatrix},
X = ⎣ ⎢ ⎢ ⎢ ⎡ X 1 ( 1 ) X 1 ( 2 ) . . . X 1 ( m ) X 2 ( 1 ) X 2 ( 2 ) . . . X 2 ( m ) . . . . . . . . . . . . X n ( 1 ) X n ( 2 ) . . . X n ( m ) ⎦ ⎥ ⎥ ⎥ ⎤ , θ = ⎣ ⎢ ⎢ ⎡ θ 1 θ 2 . . . θ n ⎦ ⎥ ⎥ ⎤ , y = ⎣ ⎢ ⎢ ⎡ y 1 y 2 . . . y m ⎦ ⎥ ⎥ ⎤ ,