吴恩达-机器学习(2)-多元线性回归、正规方程

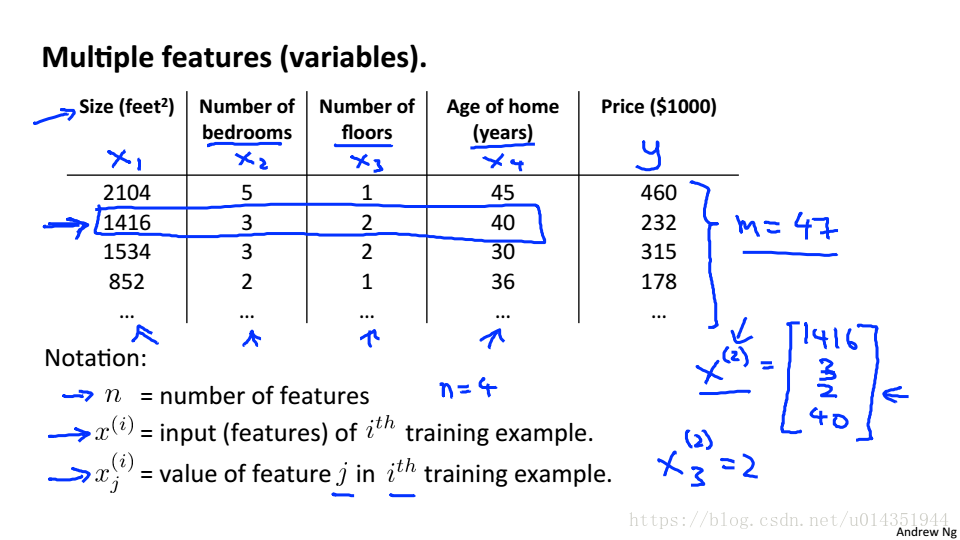
Multivariate Linear Regression

n:特征的个数
$x^{(i)}$：第i个训练样本的输入特征值
$x^{(i)}_j$:第i个训练样本的第j个特征值
当有多个特征的时候，假设函数就是如下公式，其中 $x_0$=1

当有多个特征时，代价函数如下：
$J(\theta_0,\theta_1...\theta_n)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
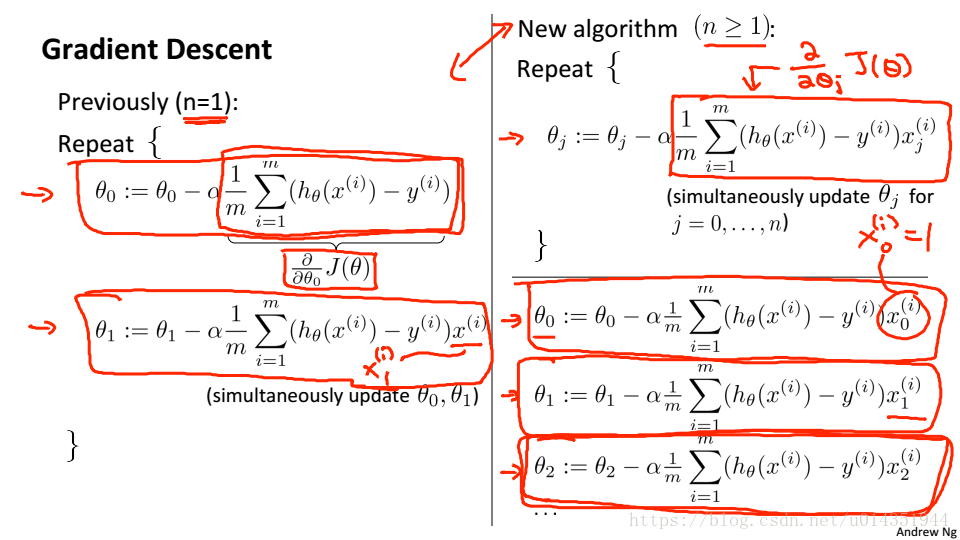
梯度下降算法也发生变化

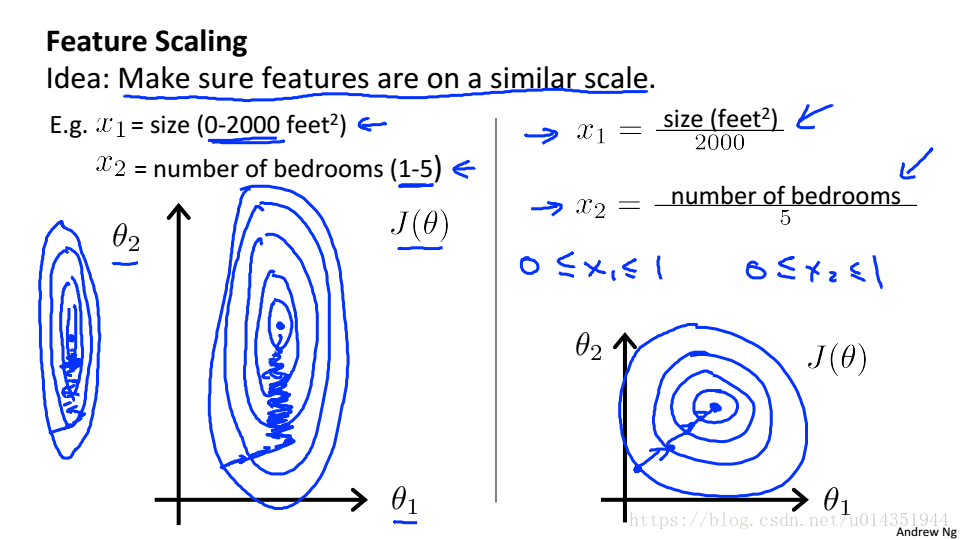
特征缩放

假设有两个特征，面积(0-2000m2)和房间数(1-5)，面积比房间数大很多，这就会导致代价函数的图形是椭圆形，进行梯度下降需要花很长时间，才能收敛。所以将两个特征均按比例缩放，使得他们在0-1之间，这样梯度下降就会很快收敛。

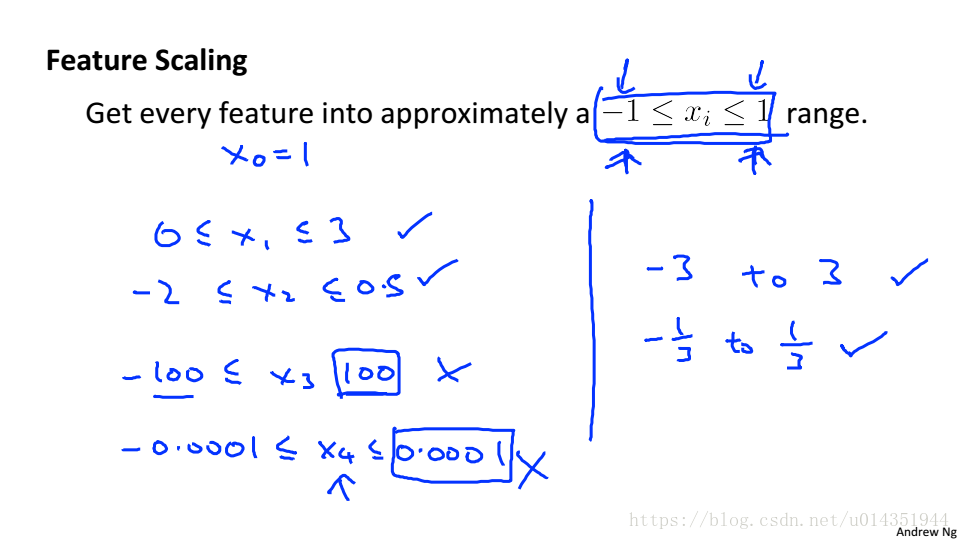
通常将特征缩放到-1~1之间

均值归一化

$u_1$:平均值 $s_1$:最大值-最小值

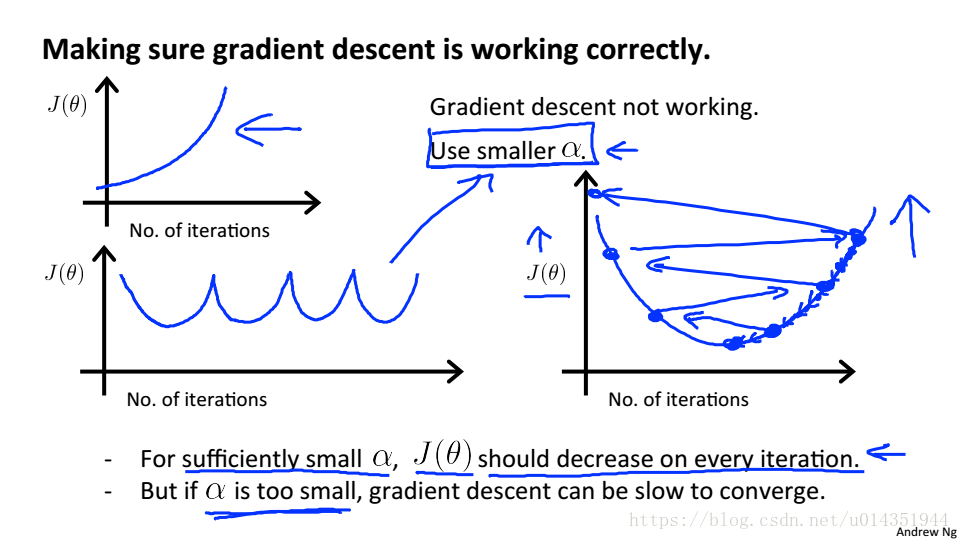
学习率

当J的减小小于 $10^{-3}$时可以看做收敛

当 $\alpha$过小，收敛的速度回很慢
当 $\alpha$过大，J在每一步迭代中可能不会总是减小,可能导致无法收敛
为了选择 $\alpha$，应该从小到大选

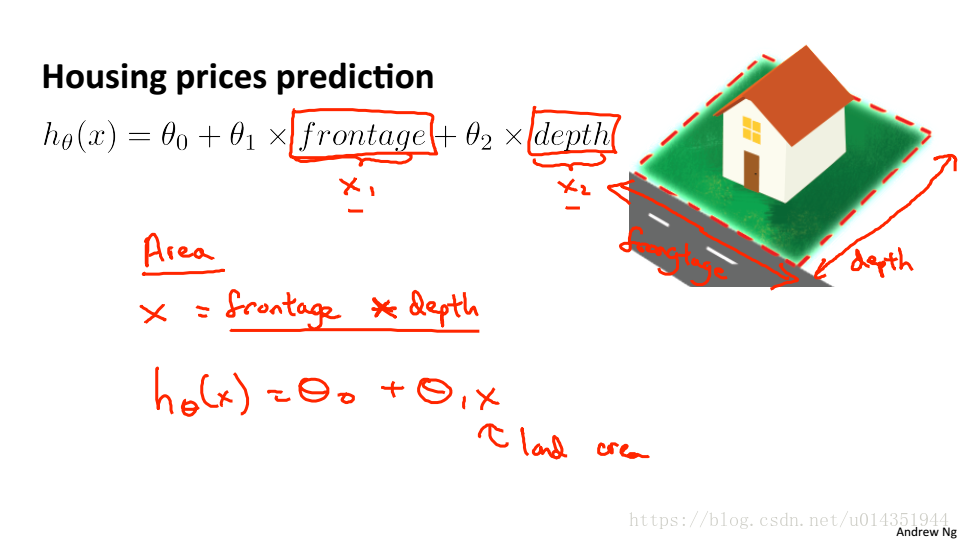
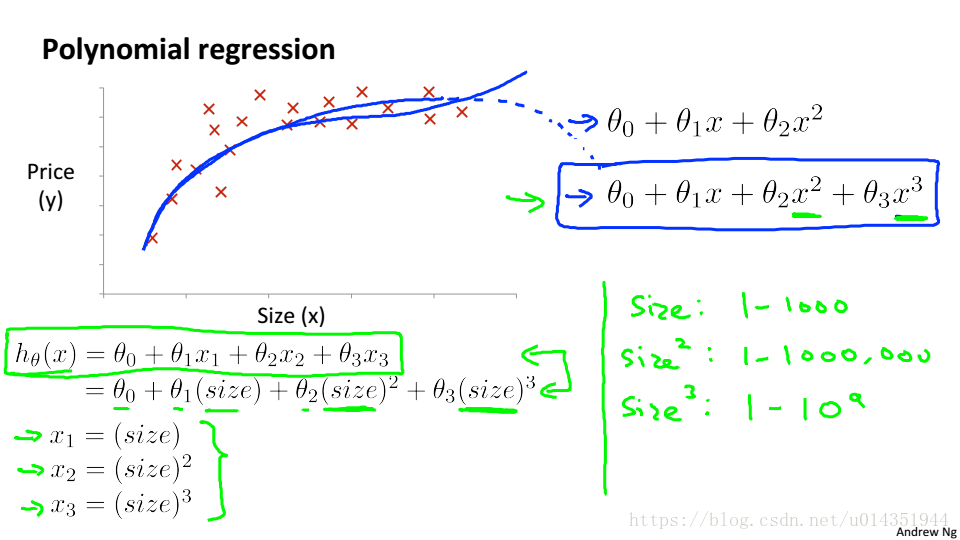
多项式回归(Ploynomial regression)

房价预测，现在有特征frontage和depth,这是可以使用两个特征的乘积(房屋的占地面积)作为新的特征进行预测

当线性回归不能很好的拟合数据，就可使用其它形式的函数

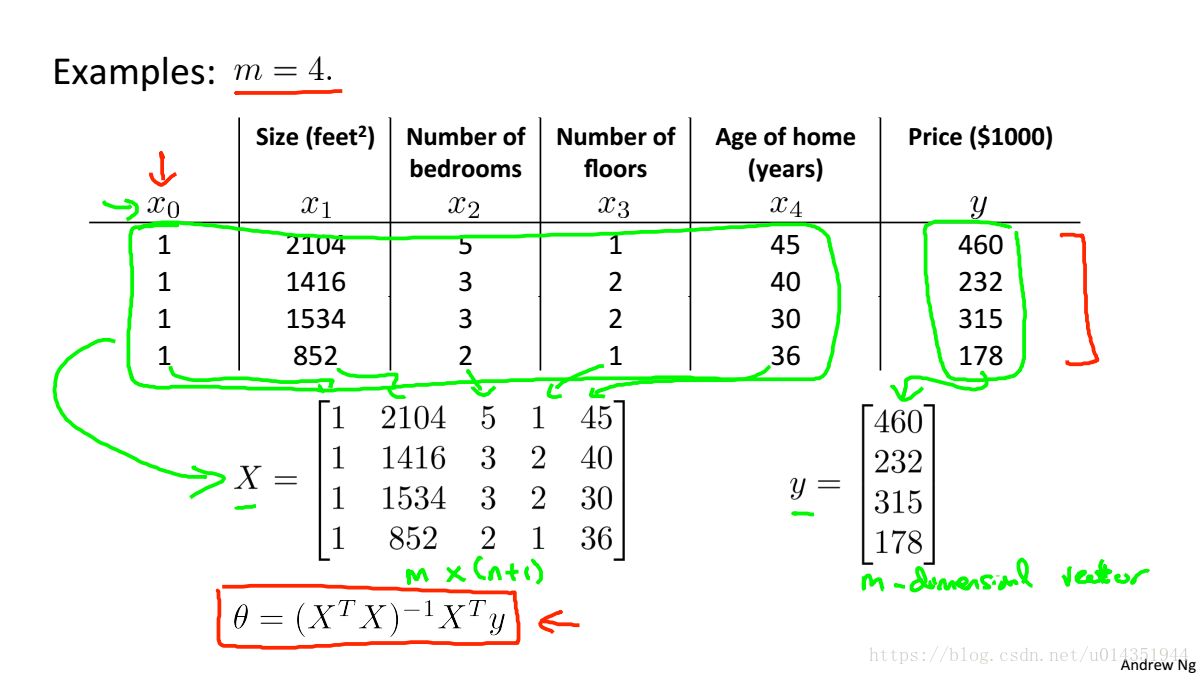
Normal Equation(正规方程)

梯度下降给出了一种最小化j的方法，让我们讨论第二种方法，这一次是显式地执行最小化，而不求助于迭代算法。在“正规方程”方法中，我们将通过显式地对J的导数，把J设为零，从而最小化J。这使我们能够在没有迭代的情况下找到最优的theta。
下面举一个例子：

梯度下降	正规方程
需要选择学习率	不需要
需要迭代	不需要
O( $kn^2$)	O( $n^3$)
当特征数量n很大，也能正常工作	当n很大是，速度会很慢

当矩阵不可逆是pinv会求矩阵的伪逆矩阵

造成 $X^TX$不可逆的两个原因：

• 冗余特性，其中两个特性是紧密相关的（即它们是线性相关的）
• 太多的特性（例如，m<=n）。