# MCMC 浅谈
1. 采样(sampling)是什么
MCMC在采样算法中有着举足轻重的地位,那么什么是采样?采样就是根据某种分布生成样本。举个例子,线性同余发生器就是根据均匀分布生成样本,这就很简单的采样了。
2. 蒙特卡罗算法
假设现在我们有个如下所示的定积分需要进行计算,
\[ \theta = \int_{a}^{b}f(x)dx \]
但是\(f(x)\)的原函数却非常难以获得。这时候采用蒙特卡罗算法进行随机模拟可以得到近似解。假设我们的函数图像如下图所示
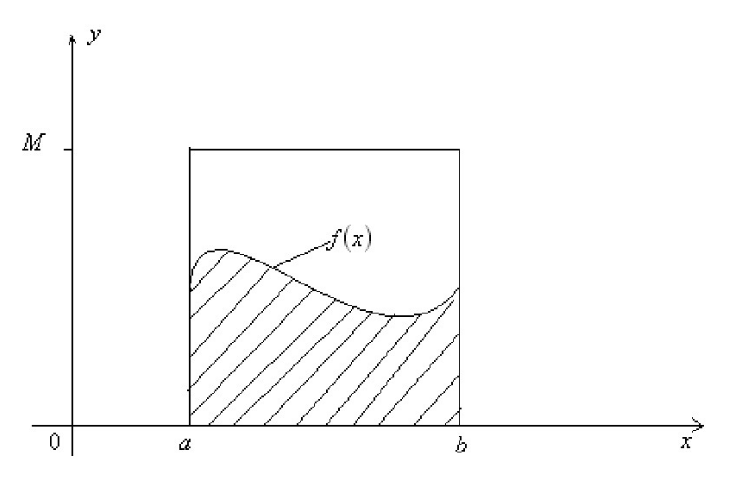
我们可以在\([a,b]\)之间随机生成一个点\(x_0\),然后可以得到\(f(x_0)\)。假设\([a,b]\)间的所有结果都是\(f(x_0)\),那么上式的积分结果可以用下式表达
\[ \int_a^bf(x)dx \approx (b - a)f(x_0) \]
此时的\(f(x_0)\)实际上相当于高,\(b - a\)就相当于底边。用\(f(x_0)\)表示\([a,b]\)区间所有的值显然过于粗糙,那么我们可以生成\(n\)个样本,用这\(n\)个样本的均值来计算积分。因为积分是在计算阴影部分的面积,那么积分的结果可以表示成下式
\[ \int_a^bf(x)dx \approx \dfrac{(b - a)}{n}\sum_{i=0}^{n-1}f(x_i) \]
此时的\(\dfrac{\sum_{i=0}^{n-1}f(x_i)}{n}\)可以看成是高。\(n\)越大,模拟得到的结果就更加贴近真实积分值。
虽然上面的方法可以一定程度上求解出近似的解,但是它隐含了一个假定,即\(x\)在\([a,b]\)之间是均匀分布的,而绝大部分情况,\(x\)在\([a,b]\)之间不是均匀分布的。如果我们用上面的方法,则模拟求出的结果很可能和真实值相差甚远。如果我们可以得到\(x\)\(在[a,b]\)的概率分布函数\(p(x)\),那么我们的定积分求和可以这样进行:
\[ \theta =\int_a^bf(x)dx=\int_a^b\dfrac{f(x)}{p(x)}p(x)dx = \dfrac{1}{n}\sum_{i=0}^{n-1}\dfrac{f(x_i)}{p(x_i)} \]
上式最右边的这个形式就是蒙特卡罗方法的一般形式。当然这里是连续函数形式的蒙特卡罗方法,但是在离散时一样成立。可以看出,最上面我们假设\(x\)在\([a,b]\)之间是均匀分布的时候,\(p(x_i)=\dfrac{1}{(b−a)}\),代入我们有概率分布的蒙特卡罗积分的上式,可以得到:
\[ \dfrac{1}{n}\sum_{i=0}^{n-1}\dfrac{f(x_i)}{p(x_i)} = \dfrac{1}{n}\sum_{i=0}^{n-1}\dfrac{f(x_i)}{\dfrac{1}{(b−a)}} = \dfrac{(b - a)}{n}\sum_{i=0}^{n-1}f(x_i) \]