1.摘要

MCMC,也称为马尔科夫链蒙特卡洛(Markov Chain Monte Carlo)方法，是用于从复杂分布中获取随机样本的统计学算法。正是MCMC方法的提出使得许多贝叶斯统计问题的求解成为可能。MCMC方法是一类典型的在编程上容易实现，但原理的解释和理解却相对困难的统计学方法。对于这类方法，如果不能够理解其内部原理便难以在实践过程中进行应用。本文会分别就两个MC进行理论介绍，而后对MCMC方法进行阐述，最后通过实例演示应用过程。此外本文中算法示例的编程语言为R。

2.随机抽样

2.1随机性

随机性的获取实际上并不像我们以为的那样容易，计算指定一个点的概率质量（概率密度）容易，但要随机的算一堆点就要在保证随机性上做很多工作。
一条解决路径是从简单分布中抽取随机样本，然后通过某种变换映射到目标分布中去。比如服从均匀分布的样本可以通过Box-Muller变换映射到正态分布中去，那么为了获取服从正态分布的样本就可以先从均匀分布中抽样再进行变换。那么该如何从均匀分布中进行随机抽样呢？工程上可以通过线性同余发生器来生成服从均匀分布的伪随机数。事实上，许多常用分布都可以通过均匀分布变换而来。

如何手工获取随机数？

当然通常为了获取服从某个分布的样本都是直接使用现成的程序库，并不用关心程序背后的原理。但问题是在实践中并不是所有分布都能够在标准的程序库中找到相应的方法，甚至有些分布的形式都无显式的用公式进行表示。这时候MCMC就派上用场了。

3.蒙特卡洛模拟

3.1 步骤

蒙特卡洛模拟是一类通过随机抽样过程来求取最优解的方法的总称，如果建立蒙特卡洛模型的过程没有出错，那么抽样次数越多，得到的答案越精确。蒙特卡洛模拟的实现，可以归纳为如下三个步骤：

a 将欲求解问题转化为概率过程。
b 从已知分布中抽样
c 通过样本计算各类统计量，此类统计量就是欲求问题的解。

3.2 示例

3.2.1问题

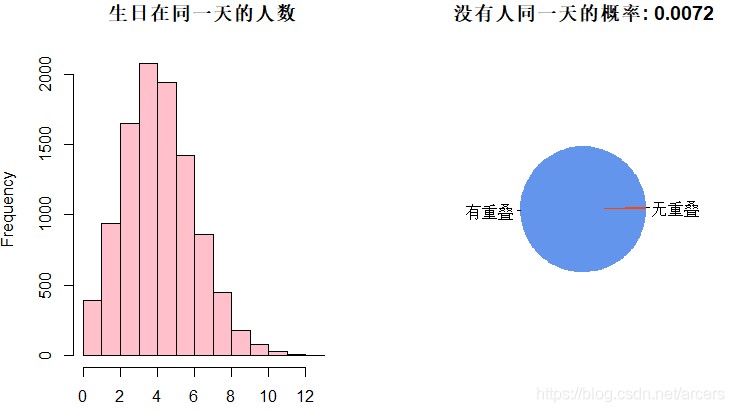
上学的时候经常听闻某某班级里有那么几个人生日居然是在同一天，感觉很巧。或许我们在一些场合下也经常遇到与自己同一天生人，通常人们都会将之解读为“缘分”。不过所谓能够得上“缘分”的事情，应该都是小概率事件，下面就用蒙特卡洛的方式算算看，到底概率几何。
问题提出：将新生随机分配，构成一个60人的班级，求解任何两个人的生日都不在同一天的概率。

3.2.2求解

构建蒙特卡洛过程：

由于学生是随机分配到一个班级的，所以每个人的出生日期是独立的，并且是从1~365之内等概率取值的。构造统计量 $B\sim P365(p1,p2,\dots,p365)，p1=p2=,\dots,p365=\frac{1}{365}$ ，则从 $P365$ 中抽样的行为可视为对学生分配到班级的模拟。那么抽样60次组成的集合就是对一个班级的模拟。因此定义一次抽样就是 $s_i=(b_{i1},\dots,b_{i60})$
重复第一步N次，N取一个足够大的数，这里暂且取N为10000。
令 $sign(s_i)=1$ 表示第i个样本中任意两个数都不相等， $sign(s_i)=0$ 表示只要有两个数相等。则有： $P(没有人的生日在同一天)\approx\frac{1}{N}\sum _{i=1}^Nsum(sign(s_i))$

prob.one <- function(n, N){
    samples <- trunc(runif(n*N,1,366))
    samples[samples == 366] <- 365
    birdays <- matrix(samples,ncol = n)
    onedayrate <- apply(birdays,1,function(x){return(n - length(unique(x)))})
    nonday <- sum(onedayrate == 0)
    par(mfrow = c(1,2))
    hist(onedayrate, breaks = 10, xlab = '', main = "生日在同一天的人数",col = "pink")
    pie(table(as.integer(onedayrate != 0)), main = paste("没有人同一天的概率:", nonday/N),
        labels = c('无重叠', '有重叠'),col = c('orangered', 'cornflowerblue'), border = NA)
}
prob.one(60, 10000)

在这里插入图片描述

4.马尔科夫链

4.1定义

4.1.1 马尔科夫性

对于随机过程，由时刻 $t_0$ 系统或过程所处状态，可以决定系统或过程在时刻 $t>t_0$ 所处状态，而无需借助 $t_0$ 以前系统或过程所处状态。即，在已知“现在”的条件下对，其“将来”不依赖于过去。
对于随机过程 $\{X(t),t\in T\}$ ,有：
$P\{X(t_n)\le x_n|,X(t_1)=x_1,X(t_2)=x_2,\dots,X(t_{(n-1)})=x_{(n-1)}\} \\ =P\{X(t_n)\le x_n|X(t_{(n-1)})=x_{(n-1)}\},x_n\in \mathbb{R}$

a 具有马尔科夫性的随机过程为马尔科夫过程。
b 时间和状态都是离散的马尔科夫过程为马尔科夫链也作马氏链。

4.1.2 转移概率矩阵

定义状态转移概率如下：
$P_{ij}(m, m + n)=P\{X_{m+n}=a_j|X_{m}=a_i\}\\ \sum_{j=i}^{+\infty}P_{ij}(m,m+n)=1,i=1,2,\dots$

由状态转移概率组成的矩阵称为转移概率矩阵 $P(m,m+n)$ 。当 $P_{ij}(m, m + n)$ 只与 $i,j,n$ 有关时，又可记为 $P_{ij}(n)$ ,此时称此转移概率具有平稳性，并且称链具有齐次性。 $P(n)$ 则称为 $n$ 步转移概率矩阵。

4.2性质

4.2.1 C-K方程

$P(u + v) = P(u)P(v)$
由此推出：
$P(n) = P(1)P(n-1)=P(1)P(1)P(n-2)=\dots=P(1)^n$
因此对于齐次马氏链，任意步长的转移概率矩阵由1阶转移概率矩阵唯一确定。

4.2.2 遍历性

若对于 $P_{ij}(n)$ 有：
$\lim_{n\to+\infty}P_{ij}(n)=\pi_j, 不依赖于i$
则称链有便利性，又若 $\sum_j\pi_j=1$ ,则称 $\pi=(\pi_1, \pi_2, \dots)$ 为链的极限分布。

定理对于其次马氏链，状态空间为 $I\in{a_1,\dots,a_N}$ ，如果存在正整数 $m$ ,对任意的 $a_i,a_j$ 有
$P_{ij}(m)>0, i,j=1,2,\dots,N$
则链具有遍历性，且具有极限分布 $\pi=(\pi_1, \pi_2, \dots)$ 。且满足： $\pi$ 是 $\pi P = P$ 的唯一非负解。

4.3示例

假设媳妇儿的心情大致可分为三种：平静、高兴、愤怒，并且每隔15分钟就会发生一次状态转移，同时下一时刻心情的变化只与上一刻的心情有关。那么根据定义，一段时间内她的心情状态就构成一条马尔科夫链。
假定这几种心情状态的一步转移概率矩阵构成如下。希望知道每天下班回家，见着她时最有可能处于那种心，好提前做好心理准备。

states_name <- c('平静', '高兴', '愤怒')
P_s1 <- matrix(
  c(0.2, 0.3, 0.5, 0.1, 0.6, 0.3, 0.4, 0.2, 0.4), ncol = 3, byrow = TRUE, 
  dimnames = list(states_name, states_name)
  )
kable(P_s1)

	平静	高兴	愤怒
平静	0.2	0.3	0.5
高兴	0.1	0.6	0.3
愤怒	0.4	0.2	0.4

随意给定初值条件进行概率推演，结果如下。

> P_s1 <- matrix(
+   c(0.2, 0.3, 0.5, 0.1, 0.6, 0.3, 0.4, 0.2, 0.4), ncol = 3, byrow = TRUE, 
+   dimnames = list(states_name, states_name)
+   )
> kable(P_s1)
> print(PI)
           平静      高兴      愤怒
 [1,] 0.7000000 0.2000000 0.1000000
 [2,] 0.2000000 0.3500000 0.4500000
 [3,] 0.2550000 0.3600000 0.3850000
 [4,] 0.2410000 0.3695000 0.3895000
 [5,] 0.2409500 0.3719000 0.3871500
 [6,] 0.2402400 0.3728550 0.3869050
 [7,] 0.2400955 0.3731660 0.3867385
 [8,] 0.2400311 0.3732760 0.3866930
 [9,] 0.2400110 0.3733135 0.3866755
[10,] 0.2400038 0.3733265 0.3866698

得知其平稳分布为 $\pi=\{\pi_{平静}=0.240, \pi_{高兴}=0.373, \pi_{愤怒}=0.387\}$ ，从而发现有0.613的概率不会挨批。于是每天携带一块秒表，进门前按下并读取毫秒数。如果数值小于0.613放心大胆进门，否则等15分钟再按一次。

5.MCMC

5.1 MCMC采样

5.1.1原理

(1)细致平稳条件

定理如果非周期马氏链的转移矩阵 $P$ 和概率分布 $\pi(x)$ 满足
$\pi(i) P_{ij} = \pi(j) P_{ji}，对任意的i,j$
则 $\pi(x)$ 为该马氏链的平稳分布。
令 $\pi(x)$ 为需要抽样的目标分布，则如果能够得到一个转移概率矩阵 $P$ 使得细致平稳条件成立，那么从一个简单分布中获取随机样本（这里简单分布指容易通过计算机程序进行直接抽样的分布，采用什么样的简单分布，视场景而定），经过 $P$ 完成若干次转移变换，则最终会到达目标分布从而完成从 $\pi(x)$ 中进行抽样。因而只要能够确定 $P$ ，就能够实现抽样。

(2)利用细致平稳条件

既然知道了细致平稳条件这一硬性标杆，即便没有条件，那就创造条件。
假设随机给定一个形式上合规的矩阵 $Q$ 作为转移矩阵,则细致平稳条件一般无法满足：
$p(i)q(i,j)\neq p(j)q(j,i)$
此时构造如下两个新变量，分别乘以等式两端。
$\alpha(i,j)=p_jq(j,i), \alpha(j,i)=p_iq(i,j)$
由于：
$p(i)q(i,j)p(j)q(j,i)=p(j)q(j,i)p(i)q(i,j)$
所以有：
$p(i)q(i,j)\alpha{(ij)}=p(j)q(j,i)\alpha{(j,i)}$

此时令:
$Q^\prime(i,j) = q(i,j)\alpha(i,j), Q^\prime(j,i) = q(j,i)\alpha(j,i)$
可知，在引入 $Q^\prime$ 的条件下，下式成立，也即细致平稳条件满足。满足了细致平稳条件，就可进行抽样了！
$p(i)Q^\prime(i,j)=p(j)Q^\prime(j,i)$

(3)理解

要理解 $Q -> Q^\prime$ 的过程是如何实现的，就是要理解 $\alpha(i,j)$ 在前后两个马氏链的变换上所起到的作用。

假设有一枚不均质的硬币， $P(X=正面)=0.6$ ，那么如何模拟一次抛掷的动作呢？如下图所示，问题等价于在[0,1]区间内，在0.6的位置将整个区间分割为[0,0.6],(0.6,1],并向其中随机撒点，任意一次撒点后点落入左侧区间，则表示正面向上，落入右侧区间则表示反面向上。随机撒点的动作，通过均匀分布抽样实现。
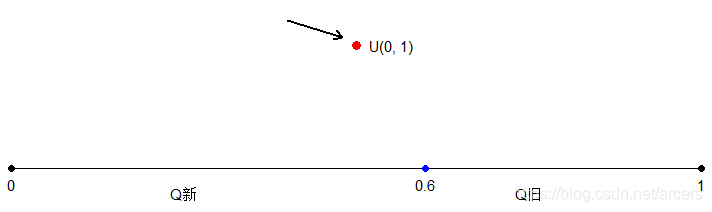
在这里插入图片描述
在这里 $\alpha(i,j)$ ，实际上就是扮演了硬币的角色，它的作用就是在保持整个抽样过程随机性的前提下，按概率实现马氏链的更新。

5.1.2算法

假设Q表示一步状态转移矩阵（对应的在连续的情况下，用D表示概率密度函数）。

a 用X表示由MCMC过程产生的状态向量， $Q_0$ 表示状态转移矩阵（ $D_0$ 表示抽样分布）。初始化 $X_0=x_0$ ，其中 $x_0$ 是从状态集（分布）中获取的随机样本。
b 对 $t = 0, 1, 2, \cdots,n$ 重复如下步骤进行采样：
- b-1 第 $t$ 时刻有 $X_t=x_t$ , 采样 $y~q(x|x_t)$ (此时状态转移矩阵为 $Q_t=q(x|x_t)$ )。
- b-2 从 $U(0,1)$ 中抽取一个样本点 $u$
- b-3 如果 $u<\alpha(x_t, y)=p(y)*q(x_t|y)$ 则接受转移 $X_{t+1}=y$
- b-4 否则拒绝转移， $X_{t+1}=x_t$ , $Q_{t+1} = Q_t$

5.2 M-H方法

5.2.1原理

由于 $\alpha(i,j)=p_{j}q(j,i) < 1$ ，通常是一个比较小的数字，因此在一次采样中很容易拒绝跳转。从而导致采样的时间成本、计算成本很高。M-H(Metropolis-Hastings)采样，通过放大跳转率 $\alpha(i,j)$ 提高了跳转概率，缩短了采样过程。
对下式两边同时除以 $p(i)q(i,j)$
$p(i)q(i,j)p(j)q(j,i)=p(j)q(j,i)p(i)q(i,j) \\ p(i)q(i,j)\frac{p(j)q(j,i)}{p(i)q(i,j)}=p(j)q(j,i)$
此时有
$\alpha(i,j)=\frac{p(j)q(j,i)}{p(i)q(i,j)},\alpha(j,i)=1$

此时，如果 $\alpha(i,j) = \frac{p(j)q(j,i)}{p(i)q(i,j)} < 1$ 则 $\alpha(i,j)$ 按照 $\alpha(j,i)$ 放大到1的比例等比例放大。但如果 $\frac{p(j)q(j,i)}{p(i)q(i,j)} > 1$ 就不行了，由于概率是不可能大于1的。那么此时就反过来,同除以 $p(j)q(j,i)$ .

$p(i)q(i,j)p(j)q(j,i)=p(j)q(j,i)p(i)q(i,j) \\ p(i)q(i,j)=p(j)q(j,i)\frac{p(i)q(i,j)}{p(j)q(j,i)}$
此时有
$\alpha(i,j) = 1,\alpha(j,i)=\frac{p(i)q(i,j)}{p(j)q(j,i)}$
当然为了跳转，需要关心的只有 $\alpha(i,j)$ ，根据以上推到新的 $\alpha(i,j)$ 可定义为：
$\alpha(i,j)=min(\frac{p(j)q(j,i)}{p(i)q(i,j)},1)$

对于新的 $\alpha$ 在取到1的情况下能实现链的满概率跳转，否则以放大 $\frac{1}{p(i)q(i,j)}$ 倍的概率进行跳转，这就是M-H方法对MCMC方法的改进。

5.2.2算法

其它不变，这里只是改变了跳转率的计算方法。

a 用X表示由MCMC过程产生的状态向量， $Q_0$ 表示状态转移矩阵（ $D_0$ 表示抽样分布）。初始化 $X_0=x_0$ ，其中 $x_0$ 是从状态集（分布）中获取的随机样本。
b 对 $t = 0, 1, 2, \cdots,n$ 重复如下步骤进行采样：
- b-1 第 $t$ 时刻有 $X_t=x_t$ , 采样 $y~q(x|x_t)$ (此时状态转移矩阵为 $Q_t=q(x|x_t)$ )。
- b-2 从 $U(0,1)$ 中抽取一个样本点 $u$
- b-3 如果$u<\alpha(x_t, y)=min(\frac{p(j)q(j,i)}{p(i)q(i,j)},1)$则接受转移$X_{t+1}=y$
- b-4 否则拒绝转移， $X_{t+1}=x_t$ , $Q_{t+1} = Q_t$

5.3 Gibbs方法

5.3.1原理

(1)M-H方法的局限

M-H方法，虽然实现了跳转率的放大，但依然不能保证100%的跳转，这就意味着总归还是要浪费不少样本，即使已经到达稳态，也还是经常要抛弃样本。这也极大的限制了M-H算法的应用范围。如果有一种方法，能够保证每次跳转都以100%的概率被接受，那就更完美的解决了这一问题。

(2)轮换采样

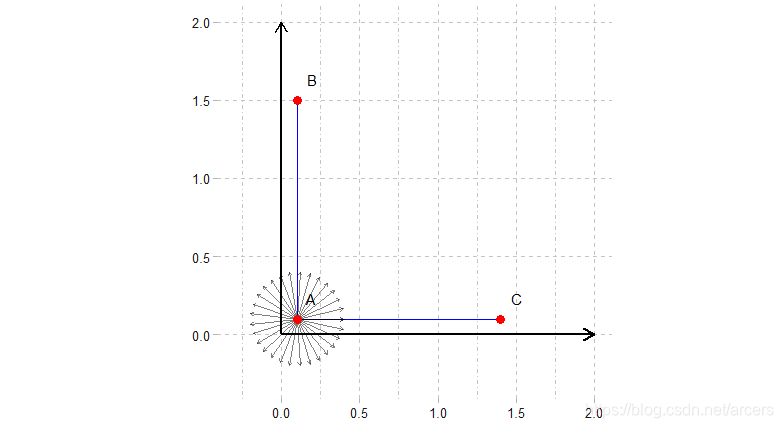
对于定义于二维空间中的马氏链，考虑如下等式：
$p(x_1, y_1)p(y_2|x_1)=p(x_1)p(y_1|x_1)p(y_2|x_1) \\ p(x_1, y_2)p(y_1|x_1)=p(x_1)p(y_2|x_1)p(y_1|x_1)$
两式右边相等，因此有：
$p(x_1, y_1)p(y_2|x_1)=p(x_1, y_2)p(y_1|x_1)$
这个等式完全满足细致平稳条件，可以实现点 $(x_1,y_1)$ 到点 $(x_1,y_2)$ 以100%的跳转率进行转换。同时可以看到转换后的两点在平行于 $y$ 轴的同一条直线上。同理可知固定 $y$ 轴而在 $x$ 轴的方向上进行采样，也同样满足细致平稳条件。因此对于二维空间中的马氏链，如下图所示，只要在两个轴的方向上进行采样就不存在拒绝跳转的问题。同理，将这一性质推广到 $N$ 维空间也是成立的。
在这里插入图片描述

5.3.2算法

以二元分布 $D(x,y)$ 为例

a 初始化 $X_0=x_0,Y_0=y_0$
b 对 $t = 0, 1, 2, \cdots,n$ 进行坐标轮换采样
- b-1 $y_{t+1}\sim p(y|x_t)$
- b-2 $x_{t+1}\sim p(x|y_{t+1})$

6.示例

6.1 M-H抽样

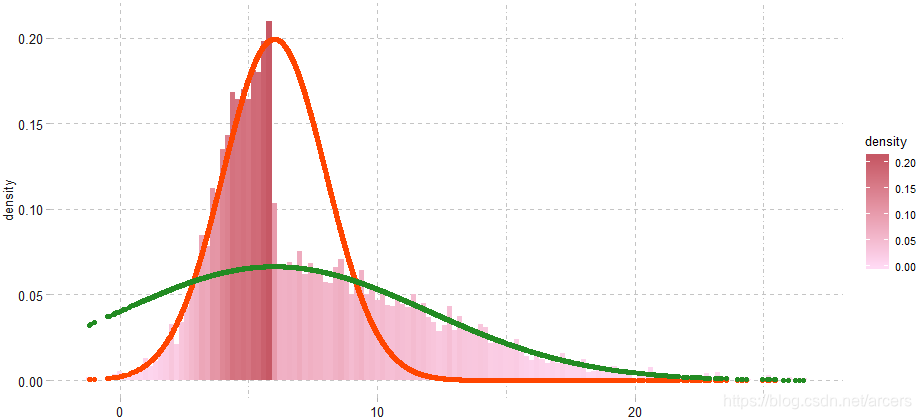
问题

使用M-H方法实现从混合正态分布中抽样。

求解

SomeDist <- function(x){
  if (x < 6) {
    res <- dnorm(x, mean = 6, sd = 2)
  } else {
    res <- dnorm(x, mean = 6, sd = 6)
  }
  return(res)
}
 
n1 = 15000  # burn in
n2 = 25000
samples <- rep(0, n1 + n2)
for (i in 1:(n1 + n2 - 1)) {
  temp <- rnorm(1,mean = samples[i], sd = 4)
  alpha <- min(1, SomeDist(temp)/SomeDist(samples[i]))
  if (runif(1, 0, 1) < alpha) {
    samples[i + 1] <- temp
  } else {
    samples[i + 1] <- samples[i]
  }
}

correct_samples <- samples[(n1 + 1):n2]

library(ggplot2)
sampledata <- data.frame(x = correct_samples)
norm1 <- data.frame(x = correct_samples, y = dnorm(correct_samples, 6, 2))
norm2 <- data.frame(x = correct_samples, y = dnorm(correct_samples, 6, 6))
ggplot() +
  geom_histogram(
    data = sampledata, 
    aes(x, y = ..density.., fill = ..density..), binwidth = 0.2
    ) +
  geom_point(data = norm1, aes(x = x, y = y), col = 'orangered') +
  geom_point(data = norm2, aes(x = x, y = y), col = 'forestgreen') +
  scale_fill_continuous_yk(isreverse = T)

在这里插入图片描述

6.2 Gibbs抽样

问题

使用Gibbs方法从二元正态分布 $N(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2,\rho)$ 中抽样

求解

按条件有随机变量 $X_1\sim N(\mu_1,\sigma_1^2)$ , $X_2\sim N(\mu_2,\sigma_2^2)$ 服从正态分布。因此 $X_1|X_2$ 以及 $X_2|X_1$ 服从正态分布，且 $X_1|X_2$ 的期望和方差为：

$E[X_1|X_2=x_2]=\mu_1 + \rho\frac{\sigma_1}{\sigma_2}(x_2 - \mu_2)\\ Var[X_1|X_2=x_2]=(1 - \rho^2)\sigma_1^2$

$X_2|X_1$ 也可类比。因此条件概率密度为：

$f(x_1|x_2)\sim N(\mu_1 + \rho\frac{\sigma_1}{\sigma_2}(x_2 - \mu_2), (1 - \rho^2)\sigma_1^2)\\ f(x_2|x_1)\sim N(\mu_2 + \rho\frac{\sigma_2}{\sigma_2}(x_1 - \mu_1), (1 - \rho^2)\sigma_2^2)$

抽样过程：

N <- 5000
N.burn <- 1000
X <- matrix(0, N, 2)
rho <- -0.6
mu1 <- 2; mu2 <- 10
sigma1 <- 1; sigma2 <- 2
s1 <- sqrt(1 - rho^2)*sigma1
s2 <- sqrt(1 - rho^2)*sigma2
X[1, ] <- c(mu1, mu2) # 用均值点作为抽样起点
for (i in 2:N) {
  if (i %% 2 == 1) {
    # 奇数步固定x2对x1采样
    x2 <- X[i - 1, 2]
    m1 <- mu1 + rho*(x2 - mu2)*sigma1/sigma2
    X[i, 1] <- rnorm(1, m1, s1)
    X[i, 2] <- x2
  } else {
    # 偶数步固定x1对x2采样
    x1 <- X[i - 1, 1]
    m2 <- mu2 + rho*(x1 - mu1)*sigma2/sigma1
    X[i, 1] <- x1
    X[i, 2] <- rnorm(1, m2, s2)
  }
}
X.samples <- X[(N.burn + 1):N,]

采样轨迹

library(ggplot2)
X.samples.df <- as.data.frame(X.samples)
names(X.samples.df) <- c('X1', 'X2')
ggplot() + geom_path(data = X.samples.df[1:500,], aes(x = X1, y = X2))

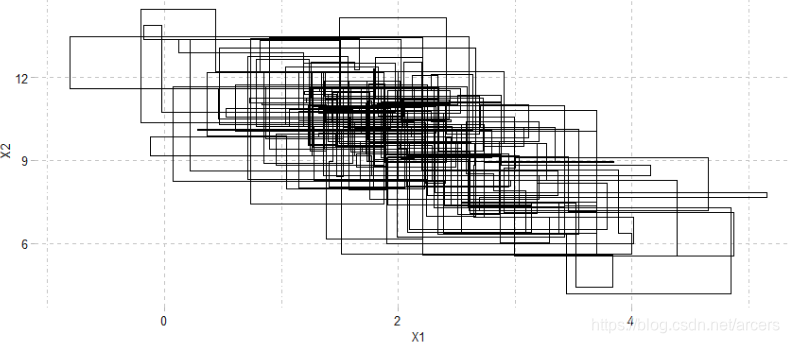
在这里插入图片描述

由于坐标轮换采样会导致相邻两个样本之间是条件独立而非完全独立的，但不相邻的样本之间是完全独立的。因此为了保证采样的随机性，仅选取奇数下标的样本作为最终的抽样结果。

> X.samples.real <- X.samples[seq(1, nrow(X.samples), by = 2),]

均值

> colMeans(X.samples.real)
[1]  1.99791 10.00917

方差

> cov(X.samples.real)
          [,1]      [,2]
[1,]  1.006575 -1.270476
[2,] -1.270476  4.290423

样本分布
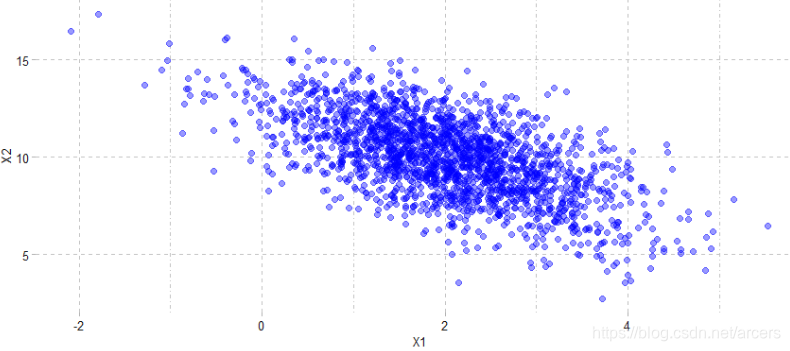
在这里插入图片描述
以上过程完演示了完整的Gibbs抽样，由于相邻样本间条件独立性的问题，更快的采样方式是在每次循环中采样完一个坐标以后，立即采样另一个坐标并将采样得到的两个坐标的新值合并为一个样本点，相当于从A点出发采样两次得到B和C，但是只存储C点（如下图所示）。

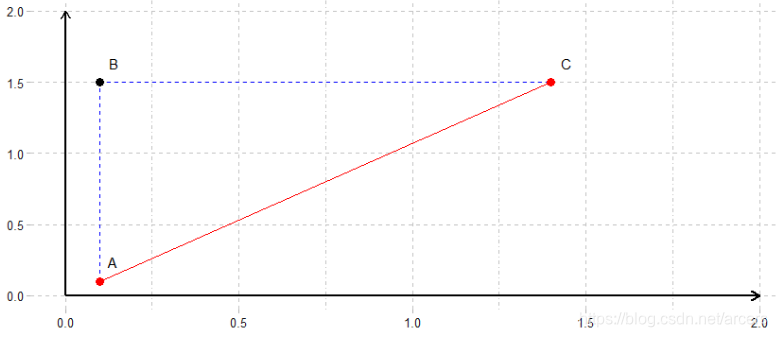
在这里插入图片描述
改进直接采样

N <- 5000
N.burn <- 1000
X <- matrix(0, N, 2)
rho <- -0.6
mu1 <- 2
mu2 <- 10
sigma1 <- 1
sigma2 <- 2
s1 <- sqrt(1 - rho^2)*sigma1
s2 <- sqrt(1 - rho^2)*sigma2
X[1, ] <- c(mu1, mu2) # 用均值点作为抽样起点

for (i in 2:N) {
  # 先固定x2对x1采样
  x2 <- X[i - 1, 2]
  m1 <- mu1 + rho*(x2 - mu2)*sigma1/sigma2
  X[i, 1] <- rnorm(1, m1, s1)
  # 再固定x1对x2采样
  x1 <- X[i, 1]
  m2 <- mu2 + rho*(x1 - mu1)*sigma2/sigma1
  X[i, 2] <- rnorm(1, m2, s2)
}

X.samples <- X[(N.burn + 1):N,]

MCMC_方法与示例

1.摘要

2.随机抽样

2.1随机性

3.蒙特卡洛模拟

3.1 步骤

3.2 示例

3.2.1问题

3.2.2求解

4.马尔科夫链

4.1定义

4.1.1 马尔科夫性

4.1.2 转移概率矩阵

4.2性质

4.2.1 C-K方程

4.2.2 遍历性

4.3示例

5.MCMC

5.1 MCMC采样

5.1.1原理

(1)细致平稳条件

(2)利用细致平稳条件

(3)理解

5.1.2算法

5.2 M-H方法

5.2.1原理

5.2.2算法

5.3 Gibbs方法

5.3.1原理

(1)M-H方法的局限

(2)轮换采样

5.3.2算法

6.示例

6.1 M-H抽样

问题

求解

6.2 Gibbs抽样

问题

求解

猜你喜欢