MCMC之蒙特卡罗方法

1.MCMC简介

马尔可夫链蒙克卡罗(Markov Chain Monte Carlo,MCMC) 是一种随机采样方法，在机器学习、深度学习及自然语言处理等领域都有广泛的应用，是很多复杂算法求解的基础，例如受限玻尔兹曼机(RBM)便是用MCMC来做一些复杂算法的近似求解。在具体讲解什么是MCMC之前，我们先看看MCMC可以解决什么样的问题，为什么需要MCMC方法。

2. 为什么需要MCMC?

假如我们需要对一维随机变量 $X$ 进行随机采样， $X$ 的样本空间是 $\{1,2,3\}$ ，概率分别是 $\{\frac{1}{2},\frac{1}{4},\frac{1}{4}\}$ 。那么我们只需要根据各离散值的概率大小对[0,1]区间进行等比例划分，例如划分为[0,0.5],[0.5,0.75],[0.75,1]三个区间，然后通过计算机产生[0,1]之间的伪随机数，根据伪随机数的落点便可完成采样。下面问题变得复杂一些，假如 $X$ 是连续分布，概率密度函数(PDF)是 $f(X)$ ，那么如何采样呢。

你肯定会想到累积分布函数(CDF)，表达式为 $P(x) = \int _{-\infty} ^{x} f(x) dx$ 。然后在[0,1]间随机生成一个数 $a$ ，求使得 $x=CDF^{-1}(a)$ ，此时便可得到一个采样结果。例如以高斯分布为例进行采样，高斯分布的概率密度函数如下所示
$f(x)= \frac{1}{\sigma \sqrt{2\pi}} exp({- \frac{(x-u)^2}{2 \sigma ^2}})$

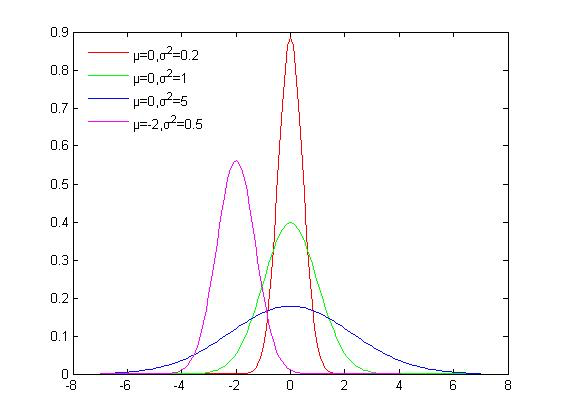
累积分布函数如下所示
$P(x) = \frac{1}{\sigma \sqrt{2\pi}} \int _{ -\infty} ^{x} exp({- \frac{(x-u)^2}{2 \sigma ^2}})dx$

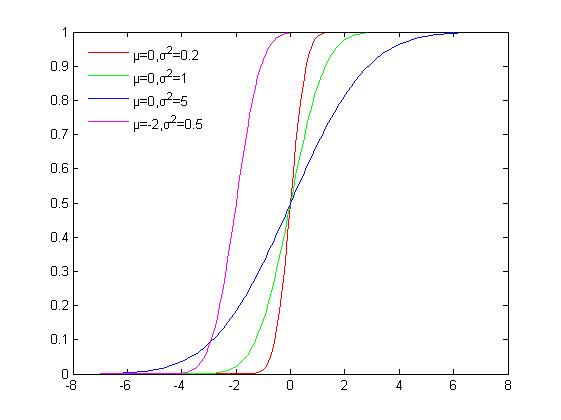
首先通过均匀分布U(0,1)得到一个值a，然后通过累积分布函数的反函数，计算得到满足 $CDF ^{-1}(x) = a$ 的x，x便是我们需要的采样样本。

上面针对连续分布采样有两个假设前提：一是概率密度函数可积；二是累积分布函数有反函数。但是上述假设前提不成立怎么办？此时便需要用到下面介绍的MCMC。

3.蒙特卡罗方法

我们首先介绍MCMC中的蒙特卡罗(Monte Carlo)方法，蒙特卡罗是一种随机模拟的方法，最初的蒙特卡罗方法是用来求解积分问题，比如
$\theta = \int _{a} ^{b} f(x) dx$

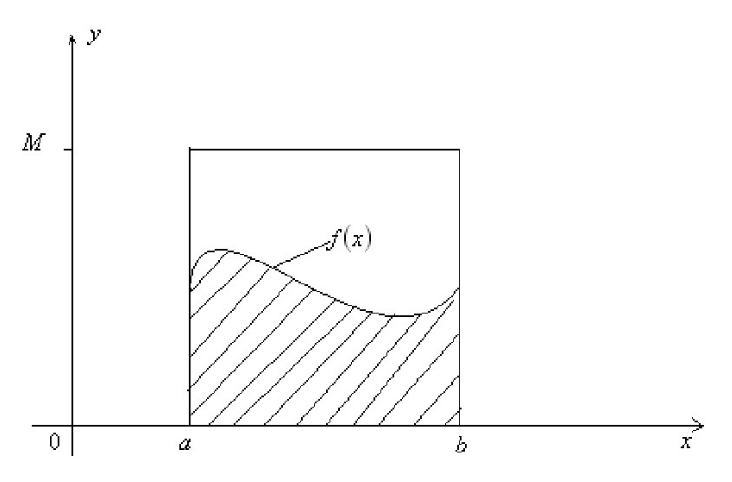
如果我们很难求解出 $f(x)$ 的原函数，那么这个积分便很难求解，此时我们便利用蒙特卡罗方法来模拟求解近似值，但如何模拟呢？针对上述积分，一个简单的近似求解方法是在[a,b]之间随机的采样一个点，比如 $x_0$ ，然后用 $f(x_0)$ 代表在[a,b]区间上所有 $f(x)$ 的值，那么上面定积分的近似值便为
$(b-a)f(x_0)$
当然，用一个值来代表[a,b]上面所有 $f(x)$ 的值，这个结果不太准确。因此我们可以采样[a,b]区间的n个值 $x_0,x_1,x_3,...,x_{n-1}$ ，用他们的均值来代表[a,b]区间上所有 $f(x)$ 的值，这样定积分求解的近似值为
$\frac{b-a}{n} \sum _{i=0}^{n-1}f(x_i)$
虽然上面的方法可以求解近似值，但它隐含一个假设，即x在[a,b]之间是均匀分布的。而大多数情况下，x在[a,b]之间不是均匀分布的，如果继续用上面的方法，模拟求出的结果很可能和结果相差甚远，那怎么解决这个问题呢？如果我们可以得到x在[a,b]的概率分布函数p(x)，那么我们的定积分求和可以转换为
$\theta = \int _{a} ^{b} f(x) dx = \int _{a} ^{b} \frac{f(x)}{p(x)}p(x)dx \approx \frac{1}{n} \sum_{i=0}^{n-1}\frac{f(x_i)}{p(x_i)}$
上述是蒙特卡罗连续函数的形式，当然在离散时一样成立。可以看出，最上面我们假设x在[a,b]之间时均匀分布的时候 $p(x_i)=\frac{1}{b-a}$ ，带入我们有概率分布的蒙特卡罗积分，可以得到
$\frac{1}{n}\sum _{i=0}^{n-1} \frac{f(x_i)}{1/(b-a)} = \frac{b-a}{n} \sum_{i=0}^{n-1}f(x_i)$
也就是说，最上面的均匀分布可以作为一般概率分布函数p(x)在均匀分布时候的特例，那么现在问题便转换为如何求出x的分布p(x)对应的若干个样本上来。

4.概率分布采样

上面讲到蒙特卡罗方法的关键是得到x的概率分布p(x)，如果求出了x的概率分布，便可以基于这个概率分布去采样n个x的样本集，然后带入蒙特卡罗求和的方程式便可以求解。当然，上面的关键问题还没有解决，即如何基于概率分布去采样n个x的样本集。

对于常见的均匀分布uniform(0,1)是非常容易采集样本的，一般通过线性同余发生器便可以很方便的生成(0,1)之间的伪随机数样本。对于常见的概率分布，无论是离散的分布还是连续的分布，都可以通过uniform(0,1)的样本转换得到。比如二维正态分布的样本(Z1,Z2)，可以通过独立采样得到uniform(0,1)样本对(X1,X2)进行转换得到，转换方程式如下所示
$Z_1 = \sqrt{-2lnX_1} cos(2\pi X_2)$

$Z_2 = \sqrt{-2lnX_1} sin(2\pi X_2)$

其他的一些常见的连续分布，比如t分布,F分布,Beta分布,Gamma分布等，都可以通过类似的方式从uniform(0,1)得到的样本转换得到。不过很多时候，我们x的概率分布不是常见的分布，这意味着我们无法方便的得到这些概率分布的样本集，那这个问题怎么解决呢？

5.接受-拒绝采样

对于概率分布不是常见的分布，一个可行的方法是采用接受-拒绝采样来得到该分布的样本。既然p(x)太复杂在程序中没法直接采样，那么我们设定一个可采样的分布q(x)，比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近p(x)分布的目的，其中q(x)叫做建议分布(proposal distribution)。

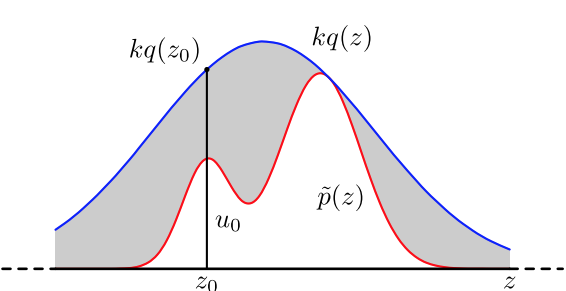
具体采样过程为，设定一个方便采样的常用概率分布q(x)以及一个常量k，使得p(x)总在kq(x)的下方，即 $k*q(z) \ge \tilde{p}(z)$ 。首先从建议分布q(z)中采样得到样本z，然后从均匀分布U(0,1)中采样得到样本u，如果 $u \le \frac{ \tilde{p}(z)}{c*q(z)}$ ，则接受此次采样，否则拒绝此次采样。整个过程中，我们通过一系列接受-拒绝采样的决策来达到用q(x)模拟p(x)概率分布的目的。

6.蒙特卡罗方法总结

使用接受-拒绝采样，可以解决一些概率分布不是常见分布的情况，然后得到采样集，最后用蒙特卡罗方法求和。但是接受-拒绝采样只能部分满足我们的情况，在很多时候我们还是很难得到概率分布的样本集，比如

对于一些二维分布(x,y)，有些时候只能得到条件概率分布p(x|y)和p(y|x)，却很难得到二维分布p(x,y)，这时便无法采用接受拒绝采样得到其样本集。
对于一些高维的复杂分布p(x1,x2,x3,…,xn)，得到合适的q(x)和k非常困难。

从上面可以看出，要将蒙特卡罗方法作为通用的采样模拟求和方法，必须解决如何方便得到各种复杂概率分布的对应采样样本的问题。下篇文章，我们将通过介绍马尔可夫链，来帮助我们找到这些复杂概率分布所对应的采样样本集。

7.推广

更多内容请关注公众号谓之小一，若有疑问可在公众号后台提问，随时回答，欢迎关注，内容转载请注明出处。