MCMC算法学习总结

1.随机模拟

随机模拟，又名蒙特卡洛方法（Monte Carlo Simulation）,发展始于20世纪40年代。
现代的统计模拟方法最早由数学家乌拉姆提出，被Metropolis命名为蒙特卡洛方法。蒙特卡洛是著名的赌场，赌博总是和统计密切相关的。布丰当年用于计算n的著名的投针试验就是蒙特卡罗模拟实验，随机采样的方法其实数学家们很早就知道，但是在计算机出现以前，随机数生成的成本很高，所以该方法也没有实用价值，随着计算机技术的迅猛发展，随机模拟技术很快进入实用阶段，对那些用确定算法不可行或不可能解决的问题，蒙特卡洛方法常常为人们带来希望。
统计模拟中有一个重要的问题就是给定一个概率分布p(x)，我们如何在计算机中生成它的样本。一般而言，均匀分布Unifrom(0,1)的样本是相对容易生成的。通过线性同余发生器可以生成伪随机数，我们用确定性算法生成[0，1]之间的伪随机数序列后，这些序列的各种统计指标和均匀分布Uniform(0,1)的理论计算结果非常接近。这样的伪随机序列就有比较好的统计性质，可以被当成真实的随机数使用。

其它常见的概率分布，无论是连续的还是离散的分布，都给予Unifrom（0，1）样本生成，正态分布可以通过著名的Box-Muller变换得到。
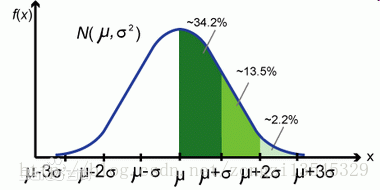
【正态分布】若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

【Box-Muller变换】
如果随机变量 U1,U2 独立且U1,U2∼Uniform[0,1]，

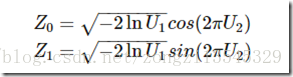
则 Z0,Z1 独立且服从标准正态分布
正态值 Z 有一个等于 0 的平均值和一个等于 1 的标准偏差，可使用以下等式将 Z 映射到一个平均值为 m、标准偏差为 sd 的统计量 X：X = m + (Z * sd)

其它几个著名的连续分布，包括指数分布、Gamma 分布、t 分布、F 分布、Beta 分布、Dirichlet 分布等等,也都可以通过类似的数学变换得到；离散的分布通过均匀分布更加容易生成。更多的统计分布如何通过均匀分布的变换生成出来，大家可以参考统计计算的书，其中 Sheldon M. Ross 的《统计模拟》是写得非常通俗易懂的一本。
不过我们并不是总是这么幸运的，当p(x)的形式很复杂，或者 p(x) 是个高维的分布的时候，样本的生成就可能很困难了。 譬如有如下的情况

1. p(x)=p~(x)∫p~(x)dx,而 p~(x) 我们是可以计算的，但是底下的积分式无法显式计算。
2. p(x,y) 是一个二维的分布函数，这个函数本身计算很困难，但是条件分布 p(x|y),p(y|x)的计算相对简单;如果 p(x) 是高维的，这种情形就更加明显。

此时就需要使用一些更加复杂的随机模拟的方法来生成样本。而本节中将要重点介绍的 MCMC(Markov Chain Monte Carlo) 和 Gibbs Sampling算法就是最常用的一种，这两个方法在现代贝叶斯分析中被广泛使用。要了解这两个算法，我们首先要对马氏链的平稳分布的性质有基本的认识。

1.2蒙特卡洛数值积分

如果我们要求f(x)的积分，如

而f(x)的形式比较复杂积分不好求，则可以通过数值解法来求近似的结果。常用的方法是蒙特卡洛积分：

这样把q(x)看做是x在区间内的概率分布，而把前面的分数部门看做一个函数，然后在q(x)下抽取n个样本，当n足够大时，可以用采用均值来近似：

因此只要q（x）比较容易采到数据样本就行了。随机模拟方法的核心就是如何对一个概率分布得到样本，即抽样（sampling）。

1.3 Monte Carlo principle

Monte Carlo 抽样计算随即变量的期望值是接下来内容的重点：X 表示随即变量，服从概率分布 p(x), 那么要计算 f(x) 的期望，只需要我们不停从 p(x) 中抽样xi，然后对这些f（xi）取平均即可近似f(x)的期望。

1.4 接受-拒绝抽样（Acceptance-Rejection sampling)

很多实际问题中，p(x)是很难直接采样的的，因此，我们需要求助其他的手段来采样。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的，其中q(x)叫做 proposal distribution 。

具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。（参考上图）

• x 轴方向：从 q(x) 分布抽样得到 a。(如果是高斯，就用之前说过的 tricky and faster 的算法更快）
• y 轴方向：从均匀分布（0, kq(a)) 中抽样得到 u。
• 如果刚好落到灰色区域： u > p(a), 拒绝， 否则接受这次抽样
• 重复以上过程

在高维的情况下，Rejection Sampling 会出现两个问题，第一是合适的 q 分布比较难以找到，第二是很难确定一个合理的 k 值。这两个问题会导致拒绝率很高，无用计算增加。

1.5 重要性抽样(Importance sampling)

Importance Sampling 也是借助了容易抽样的分布 q (proposal distribution)来解决这个问题，直接从公式出发：

很多实际问题中，p(x)是很难直接采样的的，因此，我们需要求助其他的手段来采样。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的，其中q(x)叫做 proposal distribution 。

第一个图表示 p 分布， 第二个图的阴影区域 f = 1，非阴影区域 f = 0, 那么一个良好的 q 分布应该在左边箭头所指的区域有很高的分布概率，因为在其他区域的采样计算实际上都是无效的。这表明 Importance Sampling 有可能比用原来的 p 分布抽样更加有效。

但是可惜的是，在高维空间里找到一个这样合适的 q 非常难。即使有 Adaptive importance sampling 和 Sampling-Importance-Resampling(SIR) 的出现，要找到一个同时满足 easy to sample 并且 good approximations 的 proposal distribution, it is often impossible！

1.6 马氏链及其分布

氏链是指考察一个随机过程，若己知现在t的状态X(t)，那么将来的状态X(t+n)取值（或取某些状态）的概率与过去状态X(s)（s小于t）取值无关，或更简单的说，己知现在，将来与过去无关（条件独立），则称此性质为马尔可夫性（无后效性或简称马氏性）。

马氏链的数学定义很简单

也就是状态转移的概率只依赖于前一个状态。
如图：

【转移概率矩阵】：矩阵各元素都是非负的，并且各行元素之和等于1，各元素用概率表示，在一定条件下是互相转移的，故称为转移概率矩阵。如用于市场决策时，矩阵中的元素是市场或顾客的保留、获得或失去的概率。P(k)表示k步转移概率矩阵。

举一个例子，如果当前状态为 u(x) = (0.5, 0.2, 0.3), 那么下一个矩阵的状态就是 u(x)T = (0.18, 0.64, 0.18), 依照这个转换矩阵一直转换下去，最后的系统就趋近于一个稳定状态 (0.22, 0.41, 0.37) (此处只保留了两位有效数字)。而事实证明无论你从那个点出发，经过很长的 Markov Chain 之后都会汇集到这一点。[2]

再举一个例子，社会学家经常把人按其经济状况分成3类：下层(lower-class)、中层(middle-class)、上层(upper-class)，我们用1,2,3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层的最重要的因素就是其父母的收入阶层。如果一个人的收入属于下层类别，那么他的孩子属于下层收入的概率是 0.65, 属于中层收入的概率是 0.28, 属于上层收入的概率是 0.07。事实上，从父代到子代，收入阶层的变化的转移概率如下


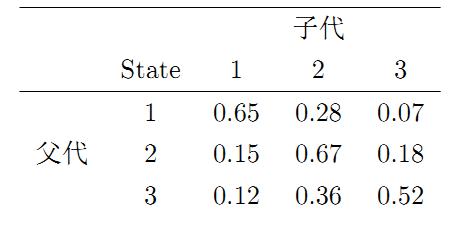
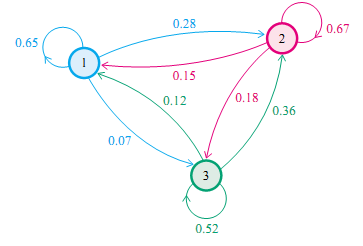
使用矩阵的表示方式，转移概率矩阵记为



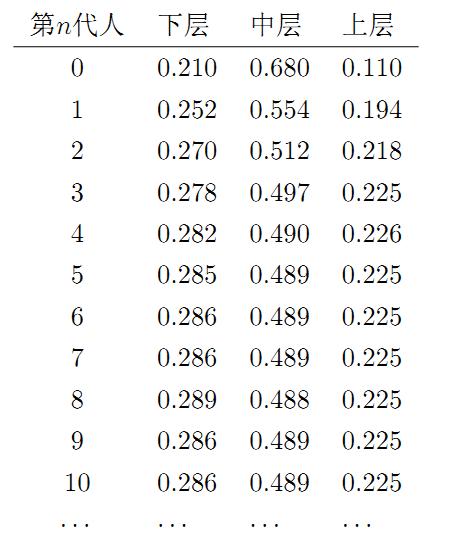
我们发现从第7代人开始，这个分布就稳定不变了，事实上，在这个问题中，从任意初始概率分布开始都会收敛到这个上面这个稳定的结果。

注：要求图是联通的（没有孤立点），同时不存在一个联通的子图是没有对外的出边的（就像黑洞一样）。

这个马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。

对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,， 如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1⋯。

这个绝妙的想法在1953年被 Metropolis想到了，为了研究粒子系统的平稳性质， Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法，即Metropolis算法，并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法，所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中， Metropolis算法也被遴选为二十世纪的十个最重要的算法之一。

我们接下来介绍的MCMC 算法是 Metropolis 算法的一个改进变种，即常用的 Metropolis-Hastings 算法。由上一节的例子和定理我们看到了，马氏链的收敛性质主要由转移矩阵P 决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵P,使得平稳分布恰好是我们要的分布p(x)。如何能做到这一点呢？我们主要使用如下的定理。


假设我们已经有一个转移矩阵Q(对应元素为q(i,j)), 把以上的过程整理一下，我们就得到了如下的用于采样概率分布p(x)的算法。

1.7 MCMC——Gibbs Sampling算法

参考资料
[1]http://blog.csdn.net/xianlingmao/article/details/7768833

[2] http://www.cnblogs.com/daniel-D/p/3388724.html

[3] http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/

[4] An Introduction to MCMC for Machine Learning，2003

[5] Introduction to Monte Carlo Methods

[6]http://www.cnblogs.com/xbinworld/p/4266146.html

2.随机模拟的R语言实现

2.1Markov Chain （马尔科夫链）

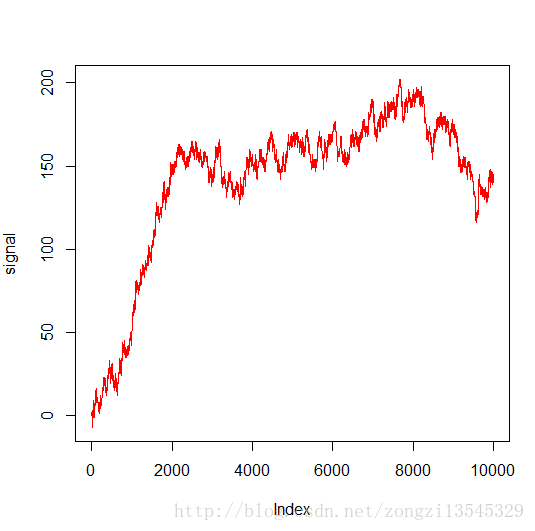
假设 f(t) 是一个时间序列，Markov Chain是假设f(t+1)只与f(t)有关的随机过程。

Implement in R:

N = 10000  
signal = vector(length = N)  
signal[1] = 0  
for (i in 2:N)  
{  
    # random select one offset (from [-1,1]) to signal[i-1]  
    signal[i] = signal[i-1] + sample(c(-1,1),1)   
}  

plot( signal,type = 'l',col = 'red') 

这里的问题：
在用RStudio运行时，会提示Error in plot.new() : figure margins too large。这个错误本质上来讲就是画的图在画布上展不开。这里有两种解决方法：
1。拖动Rstudio的画布，让画布的区域大一点。（简单粗暴。。）
2。问题在于画图时的边界空白行数（或列数）较大，因此报错。
可以用par(“mar”)查看默认的边界设置：
> par("mar")
[1] 5.1 4.1 4.1 2.1
然后在画图时，对“mar”参数进行用户自定义就可以了

opar <- par(no.readonly = TRUE)
par(mar = rep(2, 4))    # to be simple
# Plot Code
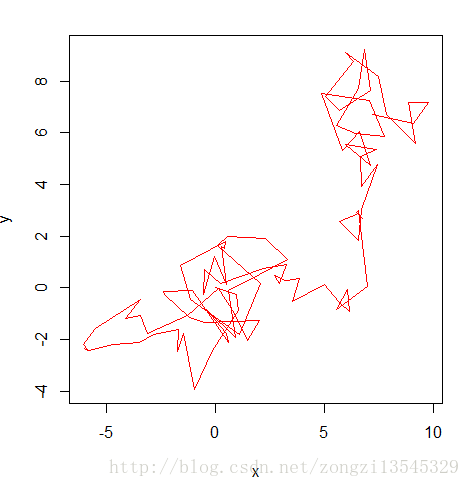
par(opar)

2.2Random Walk（随机游走）

如布朗运动，只是上面Markov Chain的二维拓展版：
Implement in R:

N = 100  
x = vector(length = N)  
y = vector(length = N)  
x[1] = 0  
y[1] = 0  
for (i in 2:N)  
{  
    x[i] = x[i-1] + rnorm(1)  
    y[i] = y[i-1] + rnorm(1)  
}  


plot(x,y,type = 'l', col='red')

2.3MCMC具体方法：

MCMC方法最早由Metropolis（1954）给出，后来Metropolis的算法由Hastings改进，合称为M-H算法。M-H算法是MCMC的基础方法。由M-H算法演化出了许多新的抽样方法，包括目前在MCMC中最常用的Gibbs抽样也可以看做M-H算法的一个特例[2]。

概括起来，MCMC基于这样的理论，在满足【平衡方程】（detailed balance equation）条件下，MCMC可以通过很长的状态转移到达稳态。
【平衡方程】：
pi(x) * P(y|x) = pi(y) * P(x|y)

其中pi指分布，P指概率。这个平衡方程也就是表示条件概率（转化概率）与分布乘积的均衡.

3.1 M-H法
1. 构造目标分布，初始化x0
2. 在第n步，从q(y|x_n) 生成新状态y
3. 以一定概率（(pi(y) * P(x_n|y)) / (pi(x) * P(y|x_n))）接受y < PS: 看看上面的平衡方程，这个概率表示什么呢？参考这里和[1]>

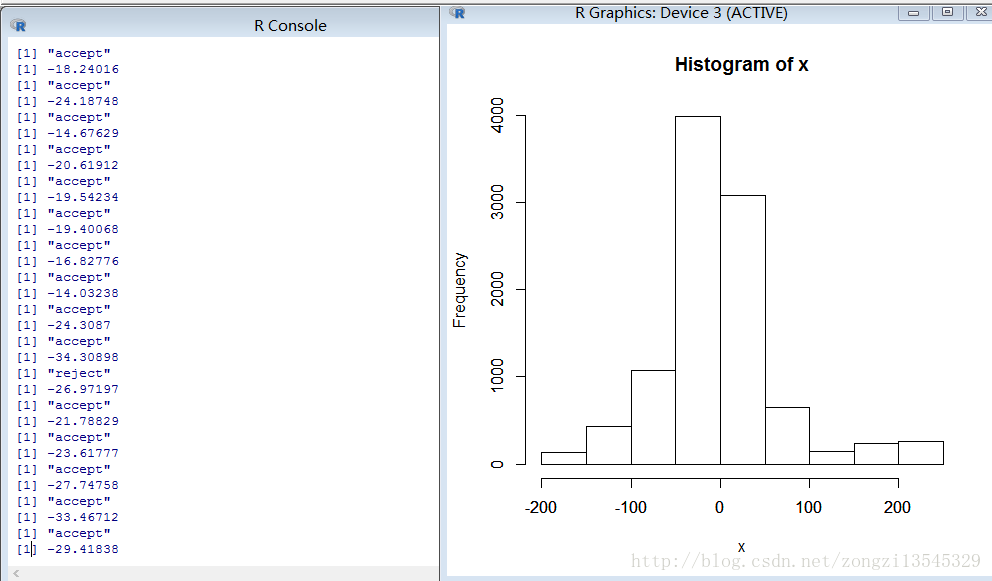
implementation in R:

N = 10000  
x = vector(length = N)  
x[1] = 0  

# uniform variable: u  
u = runif(N)  
m_sd = 5  
freedom = 5  

for (i in 2:N)  
{  
    y = rnorm(1,mean = x[i-1],sd = m_sd)  
    print(y)  
    #y = rt(1,df = freedom)  

    p_accept = dnorm(x[i-1],mean = y,sd = abs(2*y+1)) / dnorm(y, mean = x[i-1],sd = abs(2*x[i-1]+1))  
    #print (p_accept)  


    if ((u[i] <= p_accept))  
    {  
        x[i] = y  
        print("accept")  
    }  
    else  
    {  
        x[i] = x[i-1]  
        print("reject")  
    }  
}  

plot(x,type = 'l')  
dev.new()  
hist(x)  

(这里和参考代码相比少了一幅图，还在看为什么。。。。)

3.4Gibbs采样

第n次，Draw from ，迭代采样结果接近真实p

也就是每一次都是固定其他参数，对一个参数进行采样。比如对于二元正态分布，其两个分量的一元条件分布仍满足正态分布：

那么在Gibbs采样中对其迭代采样的过程，实现如下：

#define Gauss Posterior Distribution  

p_ygivenx <- function(x,m1,m2,s1,s2)  
{  
    return (rnorm(1,m2+rho*s2/s1*(x-m1),sqrt(1-rho^2)*s2 ))  
}  

p_xgiveny <- function(y,m1,m2,s1,s2)  
{  
    return  (rnorm(1,m1+rho*s1/s2*(y-m2),sqrt(1-rho^2)*s1 ))  
}  


N = 5000  
K = 20 #iteration in each sampling  
x_res = vector(length = N)  
y_res = vector(length = N)  
m1 = 10; m2 = -5; s1 = 5; s2 = 2  
rho = 0.5  
y = m2  

for (i in 1:N)  
{  
    for(j in 1:K)  
    {  
        x = p_xgiveny(y, m1,m2,s1,s2)  
        y = p_ygivenx(x, m1,m2,s1,s2)  
        # print(x)  
        x_res[i] = x;  
        y_res[i] = y;  
    }  
}  

hist(x_res,freq = 1)  
dev.new()  
plot(x_res,y_res)  
library(MASS)  
valid_range = seq(from = N/2, to = N, by = 1)  
MVN.kdensity <- kde2d(x_res[valid_range], y_res[valid_range], h = 10) #估计核密度  
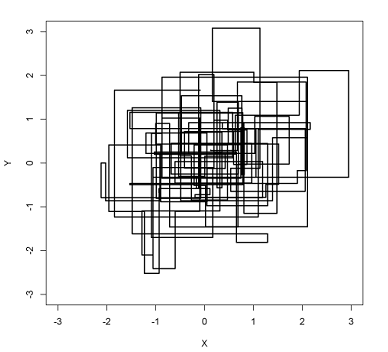
plot(x_res[valid_range], y_res[valid_range], col = "blue", xlab = "x", ylab = "y")   
contour(MVN.kdensity, add = TRUE)#二元正态分布等高线图  

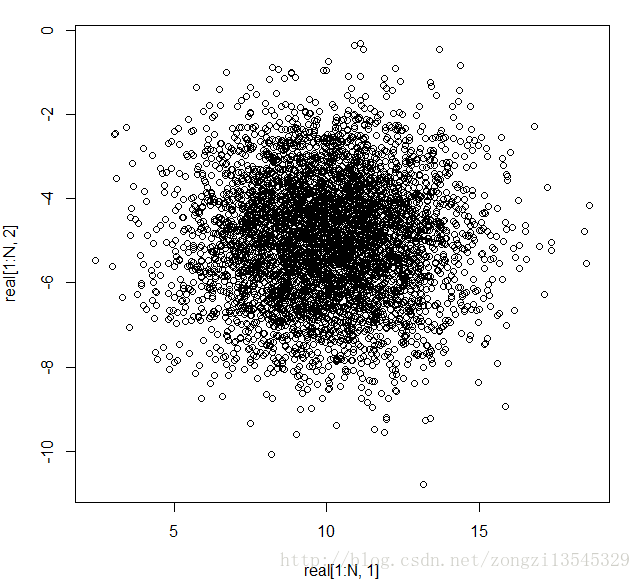
#real distribution  
 real = mvrnorm(N,c(m1,m2),diag(c(s1,s2)))  
 dev.new()  
 plot(real[1:N,1],real[1:N,2])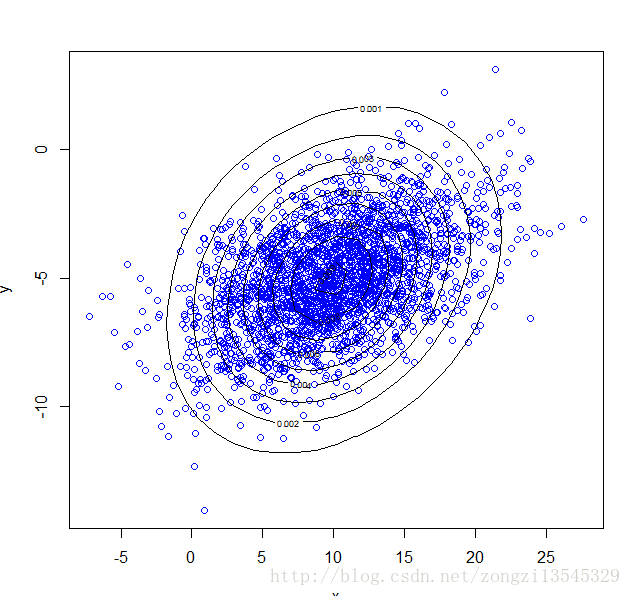  

Reference:
1.http://www2.isye.gatech.edu/~brani/isyebayes/bank/handout10.pdf
2.http://site.douban.com/182577/widget/notes/10567181/note/292072927/
3. book: http://statweb.stanford.edu/~owen/mc/
4.Classic：http://cis.temple.edu/~latecki/Courses/RobotFall07/PapersFall07/andrieu03introduction.pdf
5.https://segmentfault.com/q/1010000000575941
6.http://blog.csdn.net/abcjennifer/article/details/25908495

3 关于随机模拟和MCMC算法的个人总结和感悟

MCMC算法作为二十世纪以来最好的十大算法之一，有其突出的独特性和精妙性，被用在很多实际应用当中。

在看这个算法之前，我对统计学的相关知识和算法并没有全面和系统的了解，很多知识都是模棱两可大而化之的。所以这也导致我在算法的理论部分花费了很多时间，从一开始简单的针对性的去看这个算法本身，到为了更好的理解算法的思路而扩展开来了解更多的相关知识，并借此认真的把很多基础的概念重新整理和重温了一遍，虽然现在还是还有很多不甚明白的地方，所以以后还是要在这个领域继续深入长期的学习。

在代码实现部分，因为之前没有涉及过R语言，独立上手有些困难，所以代码主要参考了网上的部分代码，自己进行了再次实现，并对代码句段进行了个人理解。在这个过程中，也总结了一些作为一个新手在代码实现中的小问题，大部分也通过查资料和咨询同学得到了解决。目前自己也已经准备从头开始，认真细致的开始学习R语言。

在查询资料的过程中，我发现网上关于MCMC的资料并不多，而且内容很零散，针对性也比较弱，学习时会花费大量的时间。所以我站在一个有一定数学基础但是完全新手的角度上，对我能找到的一些资料（包括理论和实践部分）进行了再处理和总结，并按照我的理解对文章内容进行了重新整合和纠错，补充了相关基础知识和注意要点，最终形成了这篇学习报告。文章中提到的内容所涉及到的参考资料，也都在各部分的最后附上了链接。

文章内容也会随着我将来的深入学习，不断的进行更新和再整理。