一文弄懂动态规划（DP Dynamic Programming）下楼梯，国王和金矿，背包问题，Dijkstra算法

版权声明：知识用于传播，才是真谛，欢迎转载，注明出处就好。 https://blog.csdn.net/GhostintheCode/article/details/84837301

动态规划

参考链接

漫画算法，什么是动态规划？

DP

动态规划是一种分阶段求解决策问题的数学思想

题目一

问：下楼梯问题，有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶，请问有多少中走法。

思路

刚才这个题目，你每走一步就有两种走法，暂时不管0级到8级台阶的过程。想要走到10级，必然是从8级或者9级走的。那么问题来了，如果我们以及0到9级台阶的走法有x种，0到8级台阶有Y种，那0到10级台阶就是X+Y。

公式就是：
F（10） = F（9）+ F（8）

当只有1级台阶的时候只有一种解法，2级台阶的时候有两种方法。

递推公式就是：
F（1） = 1
F（2） = 2
F（N） = F（N-1）+ F（N-2）

动态规划的三个概念：

1. 最优子结构
2. 边界
3. 状态转移公式

当只有1级台阶或2级台阶，我们直接得出结果，无需建华，我们就成F（1）F（2）为边界。
F（N） = F（N-1）+ F（N-2）是阶段与阶段之间的状态转移公式。

求解问题

方法一：递归法

但是复杂度很高，因为当中有很多大量的重复计算。复杂度 $O(2^N)$。具体分析见开头的链接。
遇到这种情况，我们只需要创建一个哈希表，在python种建立一个字典就好了。把每次不同参数的计算结果存入哈希，当遇到相同参数时，再从哈希表里面取出，就不会重复计算了。

方法二

感觉红色箭头少了个参数。

在以上代码中，集合map是一个备忘录。当每次需要计算F(N)的时候，会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，如果map中不存在，就计算出结果，存入备忘录中

其实不用对F（N）自顶向下做递归运算，可以从下往上算。已知1，2是不是就能求3了。以此类推。

题目二

国王和金矿
问：有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？

解答

最优子结构：
10个人4金矿（第五金矿不挖的时候），10减去挖第五金矿的人数要求然后剩下4金矿（第五金矿挖的时候）。
最终问题：
10个人5金矿的最优选择。
最优子结构和最终问题的关系：
设几个变量便于描述：
N：金矿数量
W：工人人数
G[]：金矿黄金含量
P[]：金矿的用工量
关系：
F（5，10） = Max（F（4，10），F（4，10-P[4]）+ G [4]）
==> F（N，W） = Max（F（N-1，W），F（N-1，W-P[N-1]）+G[N-1]）

边界条件：

if N == 1:
	if W>= P[0]:
		return G[0]
	else:
		return 0

总结：

和之前一样，有三种实现方式，简单递归，备忘录算法，动态规划。

方法二：简单递归

把状态转移方程式翻译成递归程序，递归的结束的条件就是方程式当中的边界。因为每个状态有两个最优子结构，所以递归的执行流程类似于一颗高度为N的二叉树。方法的时间复杂度是 $O(2^N)$。

方法三：备忘录算法

在简单递归的基础上增加一个HashMap备忘录，用来存储中间结果。HashMap的Key是一个包含金矿数N和工人数W的对象，Value是最优选择获得的黄金数。方法的时间复杂度和空间复杂度相同，都等同于备忘录中不同Key的数量。

方法四：动态规划

规律

However ，当总工人数变成1000人，每个金矿的用工数也相应增加，这时候如何实现最优选择呢？

可能你觉得还是之前的动态规划方法。其实是不对的，我们可以来计算一下，
1000工人5个金矿，需要计算1000 * 5 次，需要开辟 1000 单位的空间。
然而我们用之前的简单递归，需要计算2^n次也就是32次，只需要开辟5单位（递归深度的空间）。
所以从上面计算可以知道，动态规划方法的时间和空间都和W成正比，而简单递归却与W无关，当工人数量很多的时候，动态规划反而不如递归。
（我又一个想法，思路来源于Glibc 中的 qsort() 的实现在这个链接的举例分析排序函数板块中，我的思路是这样的，两个算法都可以写在函数实现上，如果当N特别大的时候，可以选择动态规划的方法，而当N不大，而W特别大的时候，且空间有限制，此时就可以让算法退化成简单递归。不知道对不对这个思路，如果哪里考虑的不对的话，请告诉我，万分感谢）

以上就是漫画算法的全部内容。以下是我的补充内容

背包问题 和迪杰特斯拉（Dijkstra算法–求图最短路径）

背包问题

如果认真读了上面的过程，看到这个题目是不是觉得和前面矿工和金矿很像是不是。背包问题就是，钱和重量，而前面矿工和金矿问题是，钱和人数的限制。
接下来的思路是算法图解中关于动态规划的讲解，可以参考看一下。

写出正确的动态规划

Dijkstra’s Algorithm（是求从一点出发的最短路径）

伪代码

Data: G, s, dist[], pred[] and
vSet: set of vertices whose shortest path from s is unknown
Algorithm:
dist[] // array of cost of shortest path from s
pred[] // array of predecessor in shortest path from s
dijkstraSSSP(G,source):
| 	Input graph G, source node
|
|	 initialise dist[] to all ∞, except dist[source]=0
|	 initialise pred[] to all -1
| 	vSet=all vertices of G
| 	while vSet is not NULL do
|	 | 	find s in vSet with minimum dist[s]
|	 | 	for each (s,t,w) in edges(G) do
| 	 | 	relax along (s,t,w)
|	 | 	end for
| 	 | 	vSet=vSet \ {s}
|	 end while

以上伪代码仅供参考作用，喜欢的话，可以研究一下。下面通过一道题目来了解整个过程。

1. 根据伪代码进行初始化：
   
2. 根据题目的要求，从node 0开始，遍历与0相连的每条边的权重，更新列表，pred代表是从哪里来的，比如，第二列的0，代表从0来到1。（图中绿色的代表当前遍历的点）
   
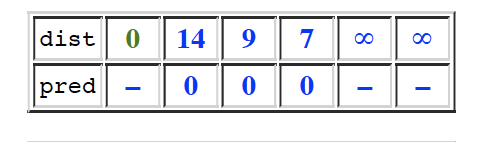
3. 然后遍历dist中除去0以外的，最小的值，以这个最小值作为起始点，遍历它连的边，更新列表。
   
4. 其实就是重复3的动作，先找剩下的最小边，遍历它连的边，更新列表，你可以动手写一下剩下的内容。当dist发生变化时，pred也要相应的发生变化，毕竟你要记录最短路径，当然要记录这个路径是从哪里来的。
   

算法复杂度分析

每条边都需要遍历一边，O（E）
外循环是遍历所有点，则是O（V）
“find s in vSet with minimum dist[s]” 这段代码
尝试找s in vSet，cost为O（V）
==>overall cost 为 $O（E+V^2） = O（V^2）$
如果用优先队列来实现找最小距离，那么
Overall cost = $O（E+VlogV）$