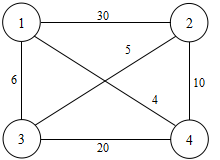
旅行售货员问题的解空间树是一颗排序树。与前面关于子集树的讨论类似,实现对排列树搜索的优先队列式分支限界法也可以用两种不同的实现方式。一种是仅使用一个优先队列来存储活结点。优先队列中的每个活结点都存储从根到该活结点的相应路径。另一种是用优先队列来存储活结点,并同时存储当前已构造出的部分排列树。在这种方式下,优先队列中的活结点不必再存储从根到该活结点的相应路径,这条路径可在必要时从存储的部分排列树中获得。
输入:城市的数目n,城市a,b,以及其之间的路程d。
输出:最短的路程,最短的路径方案。

在下面的讨论中采用第一种方式。
在具体实现时,用邻接矩阵表示所给的图G。在类Traveing中用二维数组a存储图G的邻接矩阵。
template <class Type>
class Traveling
{
public:
Type BBTSP(int *v, Type **, int, Type);
private:
Type **a, //图G的邻接矩阵
NoEdge; //图G的无边标志
int n; //图G的顶点数
};
要找最小费用旅行售货员回路,选用最小堆表示活结点优先队列。最小堆中元素的类型为MinHeapNode。该类型结点包含域x,用于记录当前解;s表示结点在排列树中的层次,从排列树的根结点到该结点的路径为x[0:s],需要进一步搜索的顶点是x[s+1:n-1]。cc表示当前费用,lcost是子树费用的下界,rcost是x[x:n-1]中顶点最小出边费用和。
//队列中元素类型
template <class Type>
class MinHeapNode
{
template <class T>
friend class Traveling;
public:
bool operator < (const MinHeapNode &MH) const
{
return lcost > MH.lcost;
}
private:
Type rcost, //x[s:n-1]中顶点最小出边费用和
lcost, //子树费用的下界
cc; //当前费用
int s, //根结点到当前结点的路径为x[0:s]
*x; //需要进一步搜索的顶点是x[s+1:n-1]
};算法开始时创建一个最小堆,表示活结点优先队列。堆中每个结点的lcost值是优先队列的优先级。接着计算出图中每个顶点的最小费用出边并用Minout记录。如果所给的有向图中某个顶点没有出边,则该图不可能有回路,算法即告结束。如果每个顶点都有出边,则根据计算出的Minout作算法初始化。算法的第一个扩展结点是排列树中根结点的唯一儿子结点。在该结点处,已确定的回路中唯一顶点为顶点1.初始时有s=0,x[0]=1,x[1:n-1]=(2,3,...,n),cc=0且 ,算法中用bestc记录当前最优值。
template <class Type>
Type Traveling<Type>::BBTSP(int *v, Type **G, int tn, Type tNoEdge)
{
priority_queue<MinHeapNode<Type> > pq;
MinHeapNode<Type> E, N;
Type bestc, cc, rcost, MinSum, *MinOut, b;
int i, j;
a = G;
n = tn;
NoEdge = tNoEdge;
MinSum = 0; //最小出边费用和
MinOut = new Type[n+1]; //计算MinOut[i]=顶点i的最小出边费用
for(i = 1; i <= n; i++)
{
MinOut[i] = NoEdge;
for(j = 1; j <= n; j++)
if(a[i][j] != NoEdge && (a[i][j] < MinOut[i] || MinOut[i] == NoEdge))
MinOut[i] = a[i][j];
if(MinOut[i] == NoEdge) //无回路
return NoEdge;
MinSum += MinOut[i];
}
//初始化
E.s = 0;
E.cc = 0;
E.rcost = MinSum;
E.x = new int[n];
for(i = 0; i < n; i++)
E.x[i] = i+1;
bestc = NoEdge;
//搜索排列空间树
while(E.s < n-1) //非叶结点
{
if(E.s == n-2) //当前扩展结点是叶结点的父结点 再加2条边构成回路
{ //所构成回路是否优于当前最优解
if(a[E.x[n-2]][E.x[n-1]] != NoEdge && a[E.x[n-1]][1] != NoEdge &&
(E.cc+a[E.x[n-2]][E.x[n-1]]+a[E.x[n-1]][1] < bestc || bestc==NoEdge))
{
//费用更小的路
bestc = E.cc + a[E.x[n-2]][E.x[n-1]] + a[E.x[n-1]][1];
E.cc = bestc;
E.lcost = bestc;
E.s++;
pq.push(E);
}
else
delete []E.x; //舍弃扩展结点
}
else //产生当前扩展结点儿子结点
{
for(i = E.s+1; i < n; i++)
if(a[E.x[E.s]][E.x[i]] != NoEdge)
{
//可行儿子结点
cc = E.cc + a[E.x[E.s]][E.x[i]]; //当前费用
rcost = E.rcost - MinOut[E.x[E.s]]; //更新最小出边费用和
b = cc + rcost; //下界
if(b < bestc || bestc == NoEdge) //子树可能含最优解 结点插入最小堆
{
N.s = E.s + 1;
N.cc = cc;
N.lcost = b;
N.rcost = rcost;
N.x = new int[n];
for(j = 0; j < n; j++)
N.x[j] = E.x[j];
N.x[E.s+1] = E.x[i]; //获得新的路径
N.x[i] = E.x[E.s+1];
pq.push(N); //加入优先队列
}
}
delete []E.x; //完成结点扩展
}
if(pq.empty()) //堆已空
break;
E = pq.top(); //取下一扩展结点
pq.pop();
}
if(bestc == NoEdge) //无回路
return NoEdge;
for(i = 0; i < n; i++) //将最优解复制到v[1:n]
v[i+1] = E.x[i];
while(pq.size()) //释放最小堆中所有结点
{
E = pq.top();
pq.pop();
delete []E.x;
}
return bestc;
}算法中while循环的终止条件是排列树的叶结点成为当前扩展结点,当s=n-1时,已找到的回路前缀是x[0:n-1],它已包含图G的所有n个顶点,当s=n-1时,相应的扩展结点表示叶结点。此时该叶结点所对应的回路的费用等于cc和lcost的值。剩余的活结点的lcost值不小于已找到的回路的费用。他们都不可能导致费用更小的回路。因此已找到的叶结点所相应的回路是一个最小费用旅行售货员回路。算法可以结束。
算法的while循环体完成对排列树内部结点的扩展。对于当前扩展结点,算法分两种情况处理。
当s=n-2时,当前扩展结点是排列树中某个叶结点的父结点。如果该叶结点相应一条可行回路且费用小于当前最小费用,则将该叶结点插入到优先队列中,否则舍去该叶结点。
当s <n-2时,算法依次产生当前扩展结点的所有儿子结点。当前扩展结点所相应的路径是x[0:s],其可行儿子结点是从剩余顶点x[s+1:n-1]中选取的顶点x[i],且(x[s],x[i])是有向图G中的一条边。对于当前扩展结点的每一个可行儿子结点。计算出其前缀(x[0:s],x[i])的费用cc和相应的下界lcost。当lcost<bestc时,将这个可行儿子结点插入到活结点优先队列中。
算法结束时返回找到的最小费用,相应的最优解由数组v给出。