递归、回溯-旅行售货员问题

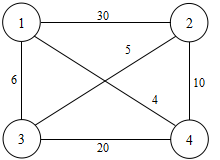
某售货员到若干城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条路线，经过每个城市一遍最后回到驻地的路线，使得总的路程(或总旅费)最小（默认从1号城市开始）。

输入：城市的数目n，城市a，b，以及其之间的路程d。

输出：最短的路程，最短的路径方案。

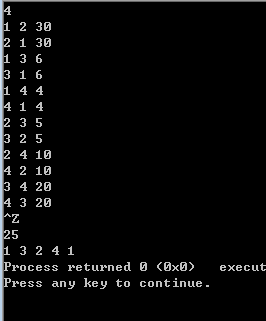
运行结果：

旅行售货员问题的解空间是一颗排列数，对于排列数的回溯搜索与生成1,2,...,n的所有排列的递归算法Perm类似。开始时x=[1,2,...n]。则相应的排列树由x[1:n]的所有排列构成。

在递归算法Backtrack中，当i=n时，当前扩展结点是排列树的叶结点的父结点。此时算法检测图G是否存在一条从顶点x[n-1]到顶点x[n]的边和一条从顶点x[n]到顶点1的边，如果这两条边都存在，则找到一条旅行售货员回路。此时，算法还需判断这条回路的费用是否优于已找到的当前最优回路的费用bestc。如果是，则必须更新当前最优值bestc和当前最优解bestx。

当i<n时，当前扩展结点位于排列数的第i-1层，图G中存在从顶点x[i-1]到顶点x[i]的边时，x[1:i]构成图G的一条路径，且当x[1:i]的费用小于当前最优值时算法进入排列树的第i层，否则将剪去相应的子树。算法用变量cc记录当前路径x[1:i]的费用。

解旅行售货员问题的回溯算法可描述如下：

template <class Type>
class Traveling
{
    template <class T>
    friend T TSP(T**, int*, int, T);
private:
    void BackTrack(int t);

    int n,                                  //城市个数
        *x,                                 //当前解，表示从解空间根结点到当前结点代表的所经过的城市
        *bestx;                             //当前最优解，已搜索的部分解空间树中费用最小周游路线对应的每一个经过的城市
    Type **a,                               //城市之间的邻接矩阵，a[i][j]表示城市i到城市j的费用，
                                            //当a[i][j]=NoEdge时，表明城市i和j无边相连
         cc,                                //当前费用，表示从解空间树根结点到当前结点代表的经过城市的费用和
         NoEdge,                            //无边标记
         bestc;                             //当前最优值，已搜索的部分解空间树中周游线路的最小费用
};
//对解空间树回溯搜索，找出周游线路额最小费用
template <class Type>
void Traveling<Type>::BackTrack(int t)
{
    int i;
    if(t == n)                                                         //当前扩展结点是排列数的叶结点的父结点
    {
         /*
         算法是否存在从城市x[n-1]到城市x[n]的边和从城市x[n]到x[1]的边，
         如果都存在，则找到一条旅行售货员的回路判断这条回路的费用是否优
         于已找到的当前最优回路费用
        */
        if(a[x[n-1]][x[n]] != NoEdge && a[x[n]][x[1]] != NoEdge &&
            (bestc==NoEdge || cc+a[x[n-1]][x[n]]+a[x[n]][1] < bestc))
        {
            bestc = cc+a[x[n-1]][x[n]]+a[x[n]][1];                     //更新当前最优解bestc
            for(i = 1; i <= n; i++)                                    //更新当前最优解bestx
                bestx[i] = x[i];
        }
        return;
    }
    //可否进入x[j]子树
    for(i = t; i <= n; i++)
        if(a[x[t-1]][x[i]] != NoEdge && (bestc==NoEdge ||   //检测是否存在一条从城市x[i-1]到城市x[j]的边
                            cc+a[x[t-1]][x[i]] < bestc))    //判断从根结点到当前搜索结点处的部分周游路线的费用
                                                            //是否小于当前找到的最小费用周游路线
        {
            //如果满足约束函数和限界函数，则搜索以当前搜索结点为根的子树
            swap(x[t], x[i]);
            cc += a[x[t-1]][x[t]];
            BackTrack(t+1);
            cc -= a[x[t-1]][x[t]];                          //回溯还原
            swap(x[t], x[i]);
        }
}
//负责变量初始化，调用递归函数Backtrack实现回溯搜索，并返回周游线路的最小费用
template <class Type>
Type TSP(Type **a, int *v, int n, Type NoEdge)
{
    Traveling<Type> Y;
    int i;

    Y.x = new int[n+1];
    //调用函数回溯搜索前要将数组x初始化为{1,2,n}
    for(i = 1; i <= n; i++)
        Y.x[i] = i;
    Y.a = a;
    Y.bestc = NoEdge;
    Y.bestx = v;
    Y.cc = 0;
    Y.n = n;
    Y.NoEdge = NoEdge;
    Y.BackTrack(2);                             //搜索x[2:n]的全排列，调用递归函数Backtrack实现回溯搜索
    delete []Y.x;

    return Y.bestc;                             //返回周游线路的最小费用
}

2、算法效率

如果不考虑更新bestx所需的计算时间，则Backtrack需要O（（n-1）！）计算时间。由于算法Backtrack在最坏情况下可能需要更新当前最优解O((n-1)!)次，每次更新bestx需O(n)计算时间，从而整个算法的计算时间复杂度为O（n！）。

递归、回溯-旅行售货员问题

猜你喜欢