本文用于复习概率论的相关知识点,因为好久不接触了,忘了不少。这里捡起来,方便学习其他知识。
总目录
本章目录
事件的运算
交换律
结合律
分配率
摩根定律
概率含义及性质
概率记为P,性质如下:
s是一个必然事件:
可列可加性:
互不相容的事件A1,A2...有:
有限可加性:
互不相容的事件A1,A2...An有:
差事件的概率
若
,则
逆事件的概率
概率的加法公式
可以推广到多个事件的情况,如下:
条件概率
条件概率的计算
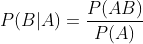
P(B|A) 表示在A空间中(A条件下),满足事件B的部分,所占的比例
条件概率的可列可加性:
互不相容的事件B1,B2...有:
条件概率的加法公式:
任意事件B1 B2,在条件A下,有:
乘法定理
由条件概率公式,可以有:
当
,有:
全概率公式
如右边这个视频,讲解得很详细了:全概率公式考研视频讲解
互不相容的事件B1 B2 ... Bn构成一个样本空间S的划分(样本空间S的完备事件集,也就是B1 B2 ... 充满了样本空间),
若A是S中的一个事件,则:
也就是A和所有B事件的交集加起来。上面是全概率公式的一种形式。
很好理解,全就是某个事件在一整个划分上,相交的部分,的总和。
根据乘法公式,可以将全概率公式改为如下变型:
贝叶斯公式
推导过程,也可以参考上面说的这个视频:全概率公式考研视频讲解
贝叶斯公式,是一个条件概率,指在条件A下,一个划分中的某个事件Bi的概率:
由条件概率公式展开有:
由于
所以,贝叶斯公式为:
很神奇,它表示在A条件下,事件Bi的概率,可以转换为,求:
- 在划分事件B1或B2或...或Bi...或Bn条件下,A事件的概率,即:P(A|B_1),...P(A|B_i),...P(A|B_n),
- 划分(完备事件集)事件B1 B2 ... Bi ... Bn的概率,即P(B_1),...P(B_i),...P(B_n),
然后把上面求得的概率,组合起来:
- 分子是Bi条件下A的概率乘以Bi的概率
- 分母是A对于划分B的全概率
这样就构成了贝叶斯公式了。
实际计算时,可能会用到很多变型,因为涉及到各种变换。所以需要具体情况具体分析。
但记住,贝叶斯公式,本质就是一个条件概率。只是把它转换成其他计算方式而已。
独立性
事件相互独立
如果A和B满足:
则A和B独立
事件独立的定理
定理一:
当P(A)>0,若A和B独立,则
反之亦然。
对于多个事件,它们的n个组合都独立,说明这堆事件相互独立。
定理二:
若A和B独立,则它们的逆事件的组合也独立,包括如下组合:
对于n个独立事件,它们逆事件的任意组合,也是独立的。

