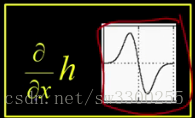
到现在为止还挺好。
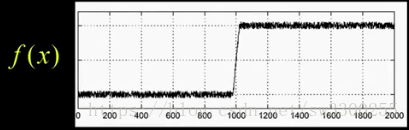
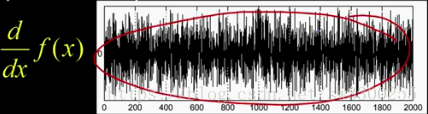
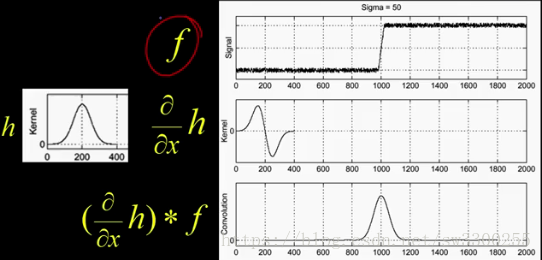
在现实世界中,在这里有这个小函数f(x):
它有一些东西,然后它需要一个跳跃,它在那里有更多的东西:
这就是强度作为x的函数。
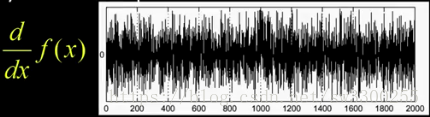
如果我实际上只是通过做一个正确的差异来获取该函数的梯度。
我要做的是,应用导数算子,得到这个:
有人可能会问,边缘在哪里。
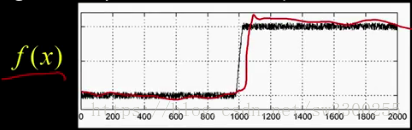
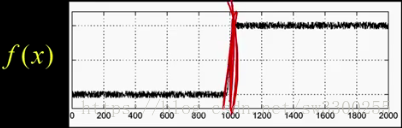
我们可以看到,这条边,哎呀,我漏了,这条边就在这里。如图:
但在这导数这个图种很混乱,很找到边缘在哪里。如图:
问题当然是我们增加了噪音。
这个噪声使得我们在各处都有正的和负的导数。
我们来看一下噪声对一些导数的影响,以及我们可以做些什么。
这里我们再次提供了更多的条纹鸭,这里我们有梯度图像:
你可以看到,当我给图像添加噪音时,我的梯度开始崩溃。
那是我开始看到这个,我有一点点高斯噪音,现在我变成了这些大椒盐噪音。
感觉像是盐和胡椒的声音,只是这些大的尖峰在我的导数中发生。
所以我们必须以某种方式处理这种噪音。
您可能知道如何处理,我们如何处理噪音?
我们过滤,我们要顺利摆脱它,我们之前做过。
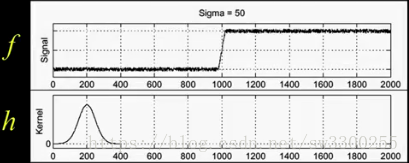
这是我的图像 f,现在让我应用一个平滑内核,h。如图:
我只是想平滑一点。所以,当我平滑它的时候,我使用这个是 h 来卷积 f 。
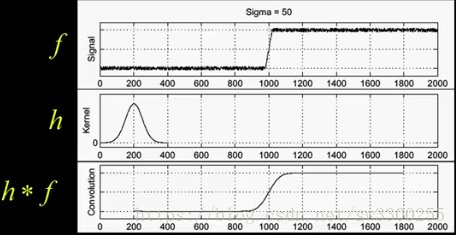
无论你是进行卷积还是相关。H 与 f 卷积,你现在看到我得到了一个漂亮,流畅的函数:
现在,我们已经平滑了信号,我们可以采取导数,你看到的是,我们得到这个好,平滑的峰值:
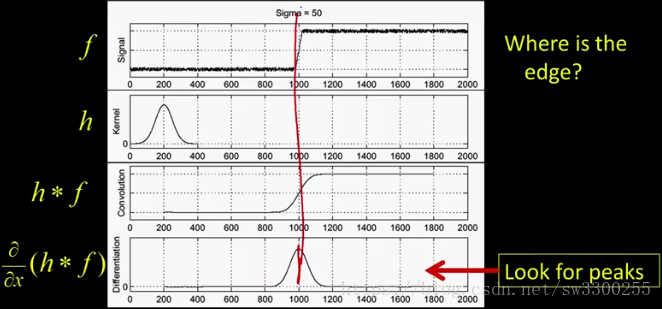
那么,边缘在哪里?
边缘将在此处达到此峰值,对应于那边的边缘。
所以基本上为了找到我们的边缘,我们将不得不以某种方式基本上应用平滑渐变并寻找一些峰值。
在我们继续这样做之前,请记住关联属性和线性等的整个概念。
我们可以自己保存一个操作,因为与f卷积的h的导数与用f卷积的h的导数相同。
那么当我们进行边缘检测时,它会是什么样子?
请继续看以下内容:
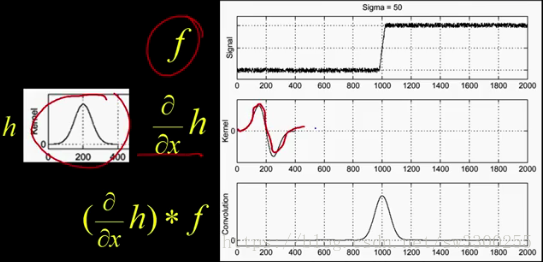
所以在这里我们拥有与以前相同的 f:
现在,我取h,然后求导,现在看起来像这样:
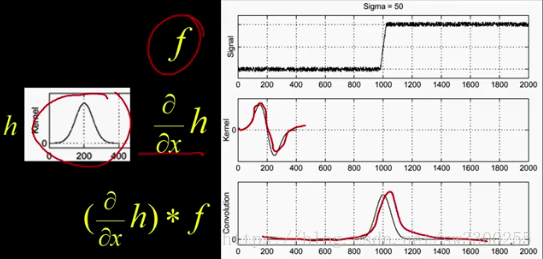
当我将该函数直接应用于f时,我得到的值与我上次得到的值相同。Wow,你会发现神奇的地方出现了:
这必须是因为线性算子的关联属性,导数和滤波是这些线性算子。
好的,最后一个问题。我们现在有这个美好的峰值:
我们必须找到峰值。我们必须找到该导数的最大值。
我们如何找到最大值?
我们取更多的导数。
所以我们将不得不采取另一种导数。
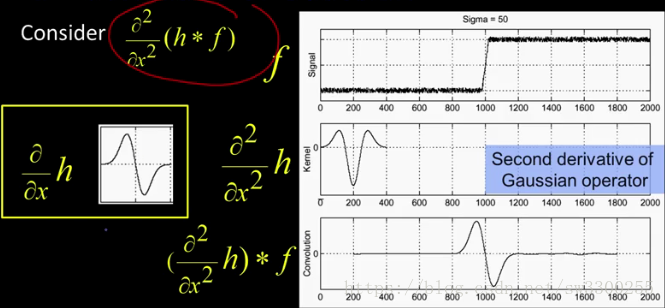
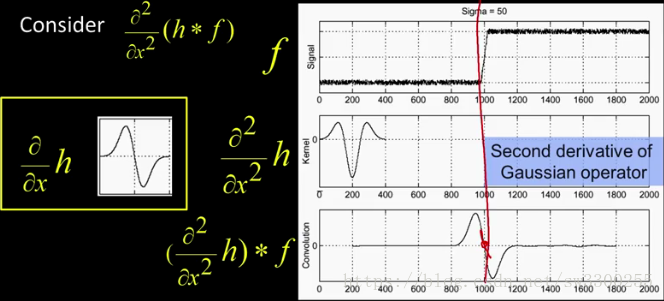
所以现在,我们只需要做一个二阶导数,而不是只做一个导数:
在h是高斯函数之前,这是高斯函数的一阶导数。
如果我们再对它求导,就会得到这个,有时被称为倒墨西哥帽。
你会看到,当我们在2D中做的时候,对吧,因为它有点像这个草帽状的,但是上下的,对吧?
当我们将该运算符应用于图像时,我们可以通过这个强斜率得到这个漂亮的零交叉:
这就是我们的边:
这是一个强力的斜率零交叉。
我们不需要找到一般的最大值,我们只需要找到任何一个值为0的地方附近有一个强梯度。
小测验:
那么我们利用了哪些线性性质首先求核的导数然后应用它,而不需要在前两个步骤中做?
A、相关;
B、可交换;
C、区分;
D、A 和 C;
答案:D。我们采用了相关,并且区分是线性的,并且可以应用相关,
这就是允许我们采用运算符的导数并将其应用于整个图像的原因。
我们稍后会谈一谈,为什么有时这是好事。
但最简单的解释是,假设我的图像是1,000 x 1,000。
假设导数是31×31。
我可以把31乘31的导数,这个很小,然后将其应用到我的1,000乘1,000。
或者,我可以把31×31应用到1000×1000上然后对整个1000×1000求导,这比对小一点的滤波器求导的计算量要大得多。
这就是我们这样做的原因之一。
——学会编写自己的代码,才能练出真功夫。