【机器学习】最小二乘法求解线性回归参数

回顾

回归分析之线性回归中我们得到了线性回归的损失函数为：
$J(\theta) = \frac{1}{2}\sum_{i=1}^m\bigg(h_\theta(x^{(i)}) - y^{(i)}\bigg)^2$

$\theta$ 的求解够

将损失函数用向量的形式表示：

$J(\theta) = \frac{1}{2}\sum_{i=1}^m\bigg(h_\theta(x^{(i)}) - y^{(i)}\bigg)^2 = \frac{1}{2}(X\theta-Y)^T(X\theta-Y)$

其中：

$h_{\theta}(x^{(i)}) = \theta_1x_1^{(i)}+\theta_2 x_2^{(i)} + ...+\theta_mx_m^{(i)}$

$X = \left [ \begin{matrix} x_1^{(1)} & x_2^{(1)} & ... & x_n^{(1)} \\ x_1^{(2)} & x_2^{(2)} & ... & x_n^{(2)} \\ && ... &\\ x_1^{(m)} & x_2^{(m)} & ... & x_n^{(m)} \\ \end{matrix} \right ]$

$\theta = \left [ \begin{matrix} \theta_1 \\ \theta_2 \\ ...\\ \theta_n \end{matrix} \right ]$

$Y= \left [ \begin{matrix} y^{(1)} \\ y^{(2)}\\ ...\\ y^{(m)} \end{matrix} \right ]$

m 表示样本的数量，n 表示每个样本的特征数量

$(i)$ 表示第 i 个样本

$X\theta = \hat{Y}$ 表示模型预测的结果， $Y$ 表示样本的真实值

损失矩阵对 $\theta$ 求导：

$\nabla_\theta J(\theta) = \nabla_\theta\Big(\frac{1}{2}(X\theta-Y)^T(X\theta-Y)\Big)$
$= \nabla_\theta\Big(\frac{1}{2}(\theta^TX^T-Y^T)(X\theta-Y)\Big)$
$= \nabla_\theta\Big(\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^TY-Y^TX\theta+Y^TY)\Big)$
$=\frac{1}{2}\Big(2X^TX\theta-X^TY-(Y^TX)^T\Big)$
$=X^TX\theta-X^TY$

令上式为0

$\theta = (X^TX)^{-1}X^TY$

最小二乘法

参数解析式：

$\theta = (X^TX)^{-1}X^TY$

最小二乘法的使用要求矩阵 $X^TX$ 是可逆的；为了防止不可逆或者过拟合的问题存在，可以增加额外数据影响，导致最终的矩阵是可逆的：

$\theta = (X^TX+\lambda I)^{-1}X^TY$

其原因在于：

$J(\theta) =\frac{1}{2}(X\theta-Y)^T(X\theta-Y) + \lambda\theta^T\theta$
$\nabla_\theta J(\theta)=X^TX\theta-X^TY+ \lambda\theta$

令上式为0：

$X^TX\theta-X^TY+ \lambda\theta = 0$
$X^TX\theta-X^TY+ \lambda\theta = 0$
$(X^TX+\lambda I)\theta= X^TY$
$\theta = (X^TX+\lambda I)^{-1}X^TY$

上面在损失函数中加入了L2-norm
最小二乘法直接求解的难点：矩阵逆的求解是一个难处

使用最小二乘法预测家庭用电（功率与电流的关系）

# 引入所需要的全部包
from sklearn.model_selection import train_test_split # 数据划分的类

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from pandas import DataFrame
import time

## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False

# 加载数据
# 日期、时间、有功功率、无功功率、电压、电流、厨房用电功率、洗衣服用电功率、热水器用电功率
path1='datas/household_power_consumption_1000.txt'
df = pd.read_csv(path1, sep=';', low_memory=False)#没有混合类型的时候可以通过low_memory=F调用更多内存，加快效率）

## 功率和电流之间的关系
X = df.iloc[:,2:4]
Y2 = df.iloc[:,5]

## 数据分割
X2_train,X2_test,Y2_train,Y2_test = train_test_split(X, Y2, test_size=0.2, random_state=0)

# 将X和Y转换为矩阵的形式
X = np.mat(X2_train)
Y = np.mat(Y2_train).reshape(-1,1)

# 计算θ
theta = (X.T * X).I * X.T * Y

# 对测试集合进行测试
y_hat = np.mat(X2_test) * theta

# 画图看看
# 电流关系
t=np.arange(len(X2_test))
plt.figure(facecolor='w')
plt.plot(t, Y2_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测值')
plt.legend(loc = 'lower right')
plt.title(u"线性回归预测功率与电流之间的关系", fontsize=20)
plt.grid(b=True)
plt.show()

运行结果：

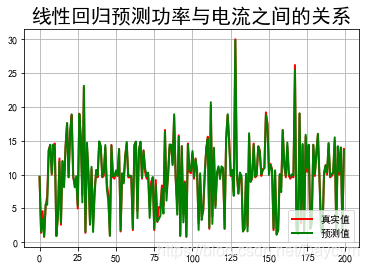
在这里插入图片描述

由高中物理可知，功率与电流之间存在固定的计算公式

代码可见: Github下01_最小二乘法.py