机器学习笔记（四）——简单线性回归&最小二乘法&多元线性回归

一、模型之母

线性回归模型可以说是最重要的数学模型之一，很多模型都是建立在它的基础之上，可以被称为是“模型之母”。

kNN算法属于分类(Classification)，即label为离散的类别型(categorical variable)，如：颜色类别、手机品牌、是否患病等。
单线性回归是属于回归(regression)，即label为连续数值型(continuous numerical variable)，如：房价、股票价格、降雨量等。

所谓简单，是指只有一个样本特征，即只有一个自变量；
所谓线性，是指方程是线性的；
所谓回归，是指用方程来模拟变量之间是如何关联的。
简单线性回归的一般形式如下，y=ax+b。y随着x的变化而变化。

二、简单线性回归模型

基本模型

y=ax+b+e

该模型也称作一元一次回归方程，模型中：
y：因变量
x：自变量
b：常数项（回归直线在y轴上的截距）
a：回归系数（回归直线的斜率）
e：随机误差（随机因素对因变量所产生的影响）
e的平方和也称为残差，残差是判断线性回归拟合好坏的重要指标之一。

则对于每个样本点 ${x_{i}}$,根据直线方程，我们可以得出
$\hat{y_{i}}=a{x_{i}}+b+{e_{i}}$

现在，我们需要寻找合适的x和y，使得所有样本点中的 ${e_{i}}$都尽可能的小，这相当于让总体的误差最小：
$e=\sum_{i=1}^{n}e_{i}=\sum_{i=1}^{n}y-\left ( a_{i}x+b_{i} \right )$
因为e有正负，取绝对值又变成了非凸函数，所以将各项取平方，我们得到了
$\sum_{i=1}^{n}\left (y-\left ( a_{i}x+b_{i} \right )\right )^{2}$

上式也被称为平方和损失函数
因此我们目标是：已知训练数据样本x、y ，找到a和b的值，使尽损失函数的值可能小，从而得出最佳的拟合方程。

三、最小二乘法

对于一个二元函数来说，最小二乘法的计算公式如下：
$J(a,b)=\sum_{i=1}^{n}\left (y_{i}-\left ( ax_{i}+b \right )\right )^{2}$
$\min_{a,b}J(a,b)$
这里J(a,b)是关于a和b的函数， $x_{i},y_{i}$的下标表示第i次测量的数据，是已知量，如果把它扩展成方程组的形式，就可以得到
$e_{1}^{2}=\left (y_{1}-\left ( ax_{1}+b \right )\right )^{2}\\ e_{2}^{2}=\left (y_{2}-\left ( ax_{2}+b \right )\right )^{2}\\ e_{3}^{2}=\left (y_{3}-\left ( ax_{3}+b \right )\right )^{2}\\ .\\ .\\e_{n}^{2}=\left (y_{n}-\left ( ax_{n}+b \right )\right )^{2}\\ J(a,b)=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+......+e_{n}^{2}$
我们的目标就是找到一组 合适的a和b，使得它们对于 整体能够有最小的误差。

计算思路

通过寻找临界点，也就是J(a,b)的偏导等于0的点，使得J（a,b）最小化：
$\frac{\partial J}{\partial a}=\sum_{i=1}^{n}2(y_{i}-(ax_{i}+b))(-x_{i})=0\\ \frac{\partial J}{\partial b}=\sum_{i=1}^{n}2(y_{i}-(ax_{i}+b))(-1)=0\\$
可以推导出
$\sum_{i=1}^{n}(x_{i}^{2}a+x_{i}b-x_{i}y_{i})=0\\ \sum_{i=1}^{n}(x_{i}a+b-y_{i})=0\\$
从而得到
$(\sum_{i=1}^{n}x_{i}^{2})a+(\sum_{i=1}^{n}x_{i})b=\sum_{i=1}^{n}x_{i}y_{i}\\ (\sum_{i=1}^{n}x_{i})a+\sum_{i=1}^{n}b=\sum_{i=1}^{n}y_{i}\\$
第二个式子还可以表示为
$a\bar{x}+b=\bar{y}$
最终可以求得
$a=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}\\ \\ b=\bar{y}-a\bar{x}$

这就是最终的方程组，方程组有唯一解。从方程组可以看到，给定的数据集不同，求出的a和b也不同。

四、损失函数及相关风险

(一) 损失函数

在机器学习中，所有的算法模型其实都依赖于最小化或最大化某一个函数，我们称之为“目标函数”。

最小化的这组函数被称为“损失函数”。什么是损失函数呢？

损失函数描述了单个样本预测值和真实值之间误差的程度。用来度量模型一次预测的好坏。

损失函数是衡量预测模型预测期望结果表现的指标。损失函数越小，模型的鲁棒性越好。

常用损失函数有：

• 0-1损失函数：用来表述分类问题，当预测分类错误时，损失函数值为1，正确为0

$L(Y,f(X))=\begin{cases} 0,& Y\neq f(X)\\ 1,& Y= f(X) \end{cases}$

• 平方损失函数：用来描述回归问题，用来表示连续性变量，为预测值与真实值差值的平方。（误差值越大、惩罚力度越强，也就是对差值敏感）
  $L(Y,f(X))=(Y-f(X))^{2}$

• 绝对损失函数：用在回归模型，用距离的绝对值来衡量
  $L(Y,f(X))=|(Y-f(X))|$

• 对数损失函数：是预测值Y和条件概率之间的衡量。事实上，该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。
  $L(Y,f(X))=-\log P(Y|X)$

以上损失函数是针对于单个样本的，但是一个训练数据集中存在N个样本，N个样本给出N个损失，如何进行选择呢？

这就引出了风险函数。

（二）期望风险

期望风险是损失函数的期望，用来表达理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。又叫期望损失/风险函数。
$R_{exp}(f)=E_{p}[L(Y,f(X))]=\int_{x\times y}L(y,f(x))F(x,y)dxdy$

（三） 经验风险

模型f(X)关于训练数据集的平均损失，称为经验风险或经验损失。

其公式含义为：模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）

$R_{emp}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))$

经验风险最小的模型为最优模型。在训练集上最小经验风险最小，也就意味着预测值和真实值尽可能接近，模型的效果越好。公式含义为取训练样本集中对数损失函数平均值的最小。
$\min_{f\in F}\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))$

（四） 经验风险最小化和结构风险最小化

期望风险是模型关于联合分布的期望损失，经验风险是模型关于训练样本数据集的平均损失。根据大数定律，当样本容量N趋于无穷时，经验风险趋于期望风险。

因此很自然地想到用经验风险去估计期望风险。但是由于训练样本个数有限，可能会出现过度拟合的问题，即决策函数对于训练集几乎全部拟合，但是对于测试集拟合效果过差。因此需要对其进行矫正：

• 结构风险最小化：当样本容量不大的时候，经验风险最小化容易产生“过拟合”的问题，为了“减缓”过拟合问题，提出了结构风险最小理论。结构风险最小化为经验风险与复杂度同时较小。
  $\min_{f\in F}\frac{1}{N}\sum_{i=1}^{N}L(y_{i},f(x_{i}))+\lambda J(f)$
  通过公式可以看出，结构风险：在经验风险上加上一个正则化项(regularizer)，或者叫做罚项(penalty) 。正则化项是J(f)是函数的复杂度再乘一个权重系数（用以权衡经验风险和复杂度）

(五)小结

1、损失函数：单个样本预测值和真实值之间误差的程度。

2、期望风险：是损失函数的期望，理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。

3、经验风险：模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）。

4、结构风险：在经验风险上加上一个正则化项，防止过拟合的策略。

五 简单线性回归的代码实现

（一）数组运算方法：

首先构造数组，并画图

import numpy as np
import matplotlib.pyplot as plt

x = np.array([1.,2.,3.,4.,5.])
y = np.array([1.,3.,2.,3.,5,])

plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()

我们就可以根据样本真实值，来进行预测。

实际上，我们是假设线性关系为：f(x)=ax+b 这根直线，然后再根据最小二乘法算a、b的值。我们还可以假设为二次函数： $f(x)=ax^2+bx+c$。可以通过最小二乘法算出a、b、c
实际上，同一组数据，选择不同的f(x)，即模型，通过最小二乘法可以得到不一样的拟合曲线。

不同的数据，更可以选择不同的函数，通过最小二乘法可以得到不一样的拟合曲线。

根据最小二乘法推导求出a、b的表达式：
$a=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}\\ \\ b=\bar{y}-a\bar{x}$
我们可以用代码计算出a,b:

# 首先要计算x和y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

# a的分子num、分母d
num = 0.0
d = 0.0
for x_i,y_i in zip(x,y):   # zip函数打包成[(x_i,y_i)...]的形式
    num = num + (x_i - x_mean) * (y_i - y_mean)
    d = d + (x_i - x_mean) ** 2
a = num / d
b = y_mean - a * x_mean

y_hat = a * x + b

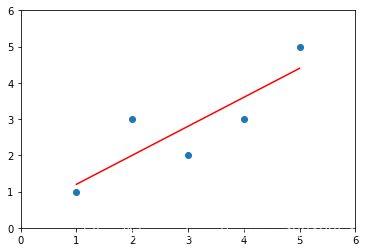
plt.scatter(x,y)    # 绘制散点图
plt.plot(x,y_hat,color='r')    # 绘制直线
plt.axis([0,6,0,6])
plt.show()

最后进行预测：

x_predict = 6
y_predict = a * x_predict + b
print(y_predict)
##输出结果为5.2

（二）向量化运算

# a的分子num、分母d
num = 0.0
d = 0.0
for x_i,y_i in zip(x,y):   # zip函数打包成[(x_i,y_i)...]的形式
    num = num + (x_i - x_mean) * (y_i - y_mean)
    d = d + (x_i - x_mean) ** 2
a = num / d

我们发现有这样一个步骤：向量w和向量v，每个向量的对应项，相乘再相加。其实这就是两个向量“点乘”

这样我们就可以使用numpy中的dot运算，非常快速地进行向量化运算。

总的来说：

向量化是非常常用的加速计算的方式，特别适合深度学习等需要训练大数据的领域。

对于 y = wx + b, 若 w, x都是向量，那么，可以用两种方式来计算，第一是for循环：

y = 0
for i in range(n):
    y += w[i]*x[i]
    y += b

另一种方法就是用向量化的方式实现：

y = np.dot(w,x) + b

二者计算速度相差几百倍，测试结果如下：

import numpy as np
import time

a = np.random.rand(1000000)
b = np.random.rand(1000000)

tic = time.time()
c = np.dot(a, b)
toc = time.time()
print("c: %f" % c)
print("vectorized version:" + str(1000*(toc-tic)) + "ms")

c = 0
tic = time.time()
for i in range(1000000):
    c += a[i] * b[i]
toc = time.time()
print("c: %f" % c)
print("for loop:" + str(1000*(toc-tic)) + "ms")

运行结果：

c: 249981.256724
vectorized version:0.998973846436ms
c: 249981.256724
for loop:276.798963547ms

对于独立的样本，用for循环串行计算的效率远远低于向量化后，用矩阵方式并行计算的效率。因此：

只要有其他可能，就不要使用显示for循环。

（三）自实现的工程文件

1.创建类

创建一个SimpleLinearRegression.py，实现自己的工程文件并调用

import numpy as np

class SimpleLinearRegression:
    def __init__(self):
        """模型初始化函数"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练模型"""
        assert x_train.ndim ==1, \
            "简单线性回归模型仅能够处理一维特征向量"
        assert len(x_train) == len(y_train), \
            "特征向量的长度和标签的长度相同"
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)
        num = (x_train - x_mean).dot(y_train - y_mean)  # 分子
        d = (x_train - x_mean).dot(x_train - x_mean)    # 分母
        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "简单线性回归模型仅能够处理一维特征向量"
        assert self.a_ is not None and self.b_ is not None, \
            "先训练之后才能预测"
        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single，返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        """返回一个可以用来表示对象的可打印字符串"""
        return "SimpleLinearRegression()"

2.调用

首先创建一组数据，然后生成SimpleLinearRegression()的对象reg1，然后调用一下

from myAlgorithm.SimpleLinearRegression import SimpleLinearRegression

x = np.array([1.,2.,3.,4.,5.])
y = np.array([1.,3.,2.,3.,5,])
x_predict = np.array([6])
reg = SimpleLinearRegression()
reg.fit(x,y)

3.输出

SimpleLinearRegression()

reg.predict(x_predict)
reg.a_

输出：array([5.2]) 0.8 0.39999999999999947

y_hat = reg.predict(x)

plt.scatter(x,y)
plt.plot(x,y_hat,color='r')
plt.axis([0,6,0,6])
plt.show()

六、多元线性回归

（一）概念

对于下面的样本数据集
$x^{(i)}=(X_{1}^{(i)},X_{2}^{(i)},…,X_{n}^{(i)},)$ 对应的是一个向量，每一行是一个样本，每列对应一个特征。对应的结果可以用如下如下公式：
$y=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+…+\theta_{n}x_{n}$
简单线性回归，只计算前两项，但是在多元线性回归中就要学习到n+1个参数，就能求出多元线性回归预测值：
$\hat{y_{i}}=\theta_{0}+\theta_{1}X_{1}^{(i)}+\theta_{2}X_{2}^{(i)}+…+\theta_{n}X_{n}^{(i)}$
也就是：第一个特征与参数1相乘、第二个特征与参数2相乘，累加之后再加上截距。就能得到预测值。
求解思路也与简单线性回归非常一致，目标同样是：
$已知训练数据样本x、y ，找到\theta_{0}, \theta_{1}，\theta_{2},…，\theta_{n}使\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})^{2}尽可能小.$
其中 $\theta=(\theta_{0},\theta_{1},\theta_{2},…,\theta_{n})$
是列向量列向量，而且我们注意到，可以虚构第0个特征X0，另其恒等于1，推导时结构更整齐，也更加方便：
$\hat{y_{i}}=\theta_{0}X_{0}^{(i)}+\theta_{1}X_{1}^{(i)}+\theta_{2}X_{2}^{(i)}+…+\theta_{n}X_{n}^{(i)}$
这样我们就可以改写成向量点乘的形式：
$X_{b}=\begin{pmatrix} 1& X_1^{(1)} & X_1^{(1)} & … &X_{n}^{(1)} \\ 1& X_1^{(2)} & X_1^{(2)} & … & X_{n}^{(2)}\\ …& & &… &… \\ 1 & X_1^{(m)} & X_1^{(m)} & … &X_{n}^{(m)} \end{pmatrix} \theta=\begin{pmatrix} \theta_0\\ \theta_1\\ \theta_2\\ …\\ \theta_{n}\end{pmatrix}$
此时可以得出：
$\hat{y}=X_b\cdot\theta$
因此我们可以把目标写成向量化的形式：
$已知训练数据样本x、y ，找到向量\theta，使(y-X_b\cdot\theta)^{T}(X_b\cdot\theta) 尽可能小.$
推导出可以得到多元线性回归的正规方程解：
$\theta=(X_b^TX_b)^{-1}X_b^Ty$

具体的推导过程可以参见《机器学习中的数学》P267。
但是这种朴素的计算方法，缺点是时间复杂度较高：O(n^3)，在特征比较多的时候，计算量很大。优点是不需要对数据进行归一化处理，原始数据进行计算参数，不存在量纲的问题（多选线性没必要做归一化处理）。

（二）多元线性回归的实现

1.创建类

下面我们来使用python代码实现多元线性回归：

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None    # 系数（theta0~1 向量）
        self.interception_ = None   # 截距（theta0 数）
        self._theta = None  # 整体计算出的向量theta

    def fit_normal(self, X_train, y_train):
        """根据训练数据X_train，y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        # 正规化方程求解
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def predict(self, X_predict):
        """给定待预测的数据集X_predict，返回表示X_predict的结果向量"""
        assert self.interception_ is not None and self.coef_ is not None, \
            "must fit before predict"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        y_predict = X_b.dot(self._theta)
        return y_predict

    def score(self, X_test, y_test):
        """很倔测试机X_test和y_test确定当前模型的准确率"""
        y_predict = self.predict(self, X_test)
        return r2_score(y_test, y_predict)
    

    def __repr__(self):
        return "LinearRegression()"

其实在代码中，思想很简单，就是使用公式即可。其中有一些知识点：

1、np.hstack(tup)：参数tup可以是元组，列表，或者numpy数组，返回结果为numpy的数组。按列顺序把数组给堆叠起来（加一个新列）。

2、np.ones()：返回一个全1的n维数组，有三个参数：shape（用来指定返回数组的大小）、dtype（数组元素的类型）、order（是否以内存中的C或Fortran连续（行或列）顺序存储多维数据）。后两个参数都是可选的，一般只需设定第一个参数。（类似的还有np.zeros()返回一个全0数组）

3、numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。inv函数计算逆矩阵

4、T：array的方法，对矩阵进行转置。

5、dot：点乘

2.调用

下面我们可以在jupyter notebook中调用我们的算法：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()

X = boston.data
y = boston.target

X = X[y<50.0]
y = y[y<50.0]

X.shape
输出：(490, 13)

y.shape
输出：(490, )

from myAlgorithm.model_selection import train_test_split
from myAlgorithm.LinearRegression import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, seed = 666)

reg = LinearRegression()
reg.fit_normal(X_train, y_train)

reg.coef_
输出：
array([-1.18919477e-01,  3.63991462e-02, -3.56494193e-02,  5.66737830e-02,
       -1.16195486e+01,  3.42022185e+00, -2.31470282e-02, -1.19509560e+00,
        2.59339091e-01, -1.40112724e-02, -8.36521175e-01,  7.92283639e-03,
       -3.81966137e-01])

reg.interception_
输出：
34.16143549622471

reg.score(X_test, y_test)
输出：
0.81298026026584658

我们看到，reg.coef_这一项的结果是13个系数，这13个系数有正有负。正负代表着该系数所乘的特征与预测目标是正相关还是负相关。正相关，特征越大房价越高；负相关，特征越大，房价越低。而系数绝对值的大小决定了影响程度。

下面我们对所有的系数按照数值由小到大进行排序：

np.argsort(reg.coef_)
输出：
array([ 4,  7, 10, 12,  0,  2,  6,  9, 11,  1,  3,  8,  5])

将这个返回结果作为索引，返回排序后索引所对应的特征名：

boston.feature_names[np.argsort(reg.coef_)]
输出：
array(['NOX', 'DIS', 'PTRATIO', 'LSTAT', 'CRIM', 'INDUS', 'AGE', 'TAX',
       'B', 'ZN', 'CHAS', 'RAD', 'RM'], dtype='<U7')

这也说明了线性回归算法，具有可解释性。

3.总结

线性回归模型有着比较清晰的数据推导过程，也是其他复杂模型的基础。
线性回归算法是典型的参数学习。
虽然线性回归只能解决回归问题，但是却是很多分类问题，如逻辑回归的基础。并且线性回归算法是假设数据是有一定的线性关系的，且线性关系越强，效果越好。