Monte Carlo Integration

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/sinat_33741547/article/details/83789151

引言

Monte Carlo Integration，即蒙特卡罗积分，这是一种很常用的数学方法，原理上也可以很直观的列出来

内容

（一）投点法求定积分

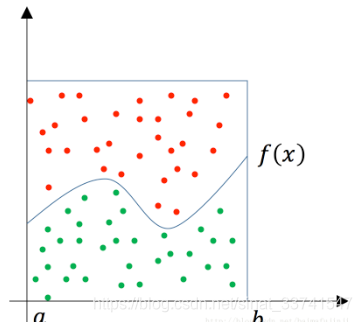
如下图，求函数f(x)从a到b的定积分。用面积为A的矩型罩在函数的积分区间上，随机地向这个矩形框里面投点，其中落在函数f(x)下方的点为绿色，其它点为红色。
统计绿色点的数量占所有点（红色+绿色）数量的比例为r，据此估算出函数f(x)从a到b的定积分为A×r。

蒙特卡洛方法能得到一个近似值，但前提是投点的方式未为真正的随机，如果必须输入一个模式中的随机数并不像设想的那样是随机数， 而却构成一些微妙的非随机模式， 那么整个的模拟（及其预测结果）都可能是错的。

（二）平均法求定积分

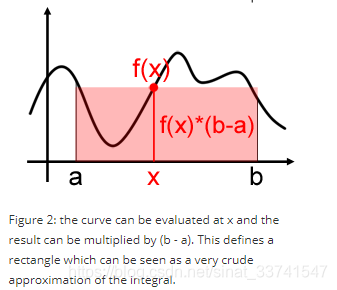
如下，存在函数f(x)，积分的几何意义就是[a,b]区间内曲线下方的面积：

如果在[a,b]之间随机取一点x，其函数值就是f(x)，那么曲线下方的面积为f(x)×(b−a)，当然很明显这种方法是很不准准确的

但在[a,b]之间随机取一系列点xi时（xi满足均匀分布），把估算出来的面积取平均来作为积分估计，这样的采样点越来越多，那么估计也就越来越接近真实值

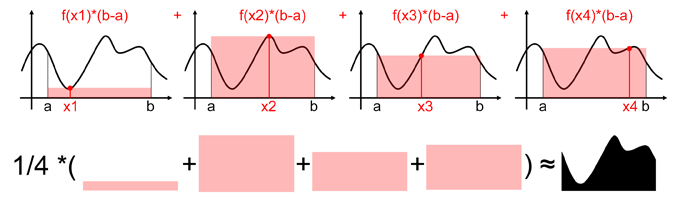
那么，可以得到公式为： $\int_a^b f(x){\rm d}x\approx\frac{b-a}{N}\sum_{i=1}^Nf(x_i)$