蒙特卡罗法 (Monte Carlo Methods)

在很多应用场景中，马尔可夫决策过程的状态转移概率 \(p(s^ {\prime}|s,a)\) 和奖励函数 \(r\left( {s,a,s^{\prime}} \right)\) 都是未知的。这种情况一般需要智能体与环境交互，然后收集一些样本，然后再根据这些样本来求解最优策略，这种基于采样的学习方法称为模型无关的强化学习 \([1]\).

1 蒙特卡罗预测 (Monte Carlo Prediction)

1.1 蒙特卡罗状态值函数估计

蒙特卡罗法通过对若干个完整的状态序列(episode)采样以获取大量的经验数据，从而来估计真实的状态值函数 \({v_\pi }\left( s \right)\).

在马尔可夫决策过程中对状态值函数 \({v_\pi }\left( s \right)\) 的定义为：

\[\begin{aligned} v_{\pi}(s) &= \mathbb{E}_{\pi}(G_t|S_t=s ) \\ &= \mathbb{E}_{\pi}(r_{t+1} + \gamma r_{t+2} + \gamma^2r_{t+3}+...|S_t=s) \end{aligned} \tag{1-1} \]

即它等于所有该状态收获的期望，而蒙特卡罗做的事是在计算值函数时，用经验平均代替随机变量的期望。比如我们在一次 episode 中，状态 \(s\) 出现后得到的收获为：

\[G_t =r_{t+1} + \gamma r_{t+2} + \gamma^2r_{t+3}+... \gamma^{T-t-1}r_{T} \tag{1-2} \]

有了一次 episode 就可以有多次，所以状态值函数 \({v_\pi }\left( s \right)\) 为：

\[v_{\pi}(s) \approx average(G_t), s.t. S_t=s \tag{1-3} \]

现在有个问题是：状态 \(s\) 可能在一个 episode 中出现不止一次，从下图中就可以看出来。图中每一行都是当前策略下的一个独立的 episode.

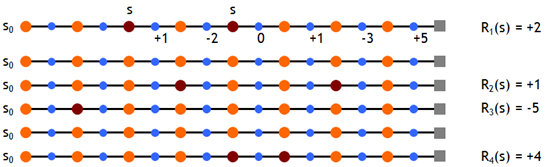
这种情况有两种处理的方式，分别为：

First-visit MC method：只把第一次出现该状态 \(s\) 后产生的 return \(G_t\) 记录下来，用于估计 \({v_\pi }\left( s \right)\)
Every-visit MC method：把所有出现该状态 \(s\) 后的 return 都记录下来，用来进行估计 \({v_\pi }\left( s \right)\)

第二种方法比第一种的计算量要大一些，但是在完整的经历样本序列少的场景下会比第一种方法适用

图中是用第一种方法计算的 return，所以 \(R_1(s)=1-2+0+1-3+5=2\). 最后得到的 \({v_\pi }\left( s \right)\) 为：

\[{v_\pi }\left( s \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{R_i}\left( s \right)} = \frac{1}{4}\left( {2 + 1 - 5 + 4} \right) = 0.5 \tag{1-4} \]

很明显生成的 episode 越多，对状态值函数 \({v_\pi }\left( s \right)\) 的估计就越准确，具体的算法流程为\([2]\)：

First-visit MC prediction

1.2 蒙特卡罗动作值函数估计

我们在使用动态规划方法进行策略改进时，是假设环境状态转移概率 \(p(s^ {\prime}|s,a)\) 是已知的，这样我们才能评判下一步采取什么 action 会更好。但是现在我们并不知道 \(p(s^ {\prime}|s,a)\)，也就没办法按以前的方法进行策略改进。

\[\begin{split}\pi^{\prime}(s)&=\arg\max_{\mathbf{a}}q_{\pi}(s,a)\\ &=\arg\max_{\mathbf{a}}\sum_{s^{\prime}}p(s^{\prime}\mid s,a)\left[r(s,a,s^{\prime})+\gamma\upsilon_{\pi}(s^{\prime})\right]\end{split} \tag{1-5} \]

所以我们不如用相同的办法直接对动作值函数 \({Q^\pi }\left( {s,a} \right)\) 进行估计：

\[{Q^\pi }\left( {s,a} \right) = \frac{1}{N}\sum\limits_{n = 1}^N {G\left( {\tau _{{s_t} = s,{a_t} = a}^{\left( n \right)}} \right)} \tag{1-6} \]

\(\tau^{(n)}\) 也就是第 \(n\) 个轨迹，也就是第 \(n\) 个 episode.

2 Monte Carlo Control

蒙特卡罗控制(Monte Carlo Control) 首要的问题就是如何估计最优策略，我们需要产生无数的 episode 才能保证收敛到最优结果。无数的 episode 和大量的迭代导致计算量巨大，效率非常低。主要有两种办法解决这个问题：

虽说理论上必须有无限个 episode 来估计 \({Q^\pi }\left( {s,a} \right)\)，实际上我们是做不到的，我们只能尽力多产生点 episode，尽可能去接近这个收敛值。我们可以设定一个误差，两次估计的值小于这个误差，差不多就行了。
在策略提升前放弃完全的策略评估，采用 episode by episode 的方式进行优化。即先用当前策略生成一个 episode，然后根据这个 episode 进行动作值函数的更新，同时更新策略，并利用更新后的策略继续生成后续的 episode。

2.1 Monte Carlo with Exploring Starts

然而我们需要考虑一个严重的问题：在所有样本片段集合中，很多 state-action 对并不出现，比如当我在一个确定的 policy下，有可能某个 state 下只出现有限的几个对应的 actions，其他的 actions 都基本不出现。这样我们根本没有 returns 去 average，怎么能估计到某些 \({Q^\pi }\left( {s,a} \right)\) 呢？

比如在下五子棋，机器如果使用greedy的方法的话，从直观上来看下的每一步棋都对当前很有利。但是一些高手，看似下了一步很不相关的棋，但是从长远来看可能是一个战略上的布局，这个不相关的棋从长远来看收益可能更大，只不过我们永远不会去走那一步棋。

为了保证策略迭代对于所有行为值有效，我们必须保证持续的探索。一种解决的方法是在状态序列开始时，每个状态行为对被选到的概率都不为 0，这种方法称为探索初值假定(exploring starts)。

下面给出 Monte Carlo with Exploring Starts 算法流程：

Monte Carlo with Exploring Starts

2.3 On-Policy 蒙特卡罗控制

Exploring start 这个方案在模拟产生 episodes 也许可行，但是在从真实经验中学习时就不可行了，因为我们无法控制 start point。

On-policy Monte Carlo Control 为了避免初始状态假定而引入了随机策略。也就是在决策的时候以一定的概率选择那些不是最大回报的行为值。这样提供了探索的可能性，保证了所有状态能被访问到。On-policy Monto Carlo 控制方法的大体思想还是 GPI，但是没有探索初值假定的条件。

On-policy first-visit MC control

记录一下疑问：这每一轮实验使用的是一个新的策略\(\pi\)产生的，而这轮实验在某个状态\((s,a)\)所带来的回报\(G\)又加入到\(Return(s,a)\)去求了平均，那最后这个\(Q(s,a)\)岂不是由多个策略共同生成的结果？还是说这个\(Return(s,a)\)在每轮进行完会清空呢？

2.4 Off-Policy 蒙特卡罗控制

一个更直截了当的方法是 off-policy：使用两个策略，一个策略用来学习最优策略，另一个则更具探索性地用来产生行为。用来学习的策略我们称之为目标策略，另一个用来生成行为的称作行为策略。

Off-policy Monte Carlo Control

3 小结

蒙特卡罗法提供了一个替代的策略评估过程。蒙特卡罗法简单地对于从状态开始的 return 取均值，而不是用模型去算每个状态的值。蒙特卡罗法区别于 DP 方法主要在两方面：

蒙特卡罗法基于采样经验，所以没有模型也可以学习
蒙特卡罗法不是 bootstrap 的，因为蒙特卡罗法不基于其他状态的值估计来更新值估计