斯坦福大学机器学习笔记——降维（PCA算法）

降维也是一种无监督学习的问题。所谓的降维，就是将高维度的数据降低到低维度空间，同时降维之后的数据又能够很好的表征原来数据的特性。
以具体的例子来说明一下什么是降维：
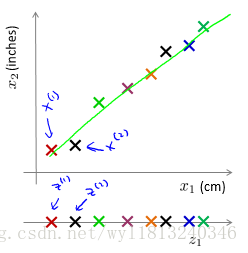
比如我们使用厘米和英尺表示同一物体的长度，如果我们使用一个仪器测量的结果单位是厘米，另一个仪器测量单位是英尺，两种仪器对同一物体测量的结果可能不完全相同（由于误差和精度），但是如果直接将两个特征都作为该物体长度的特征又很冗余，所以我们可以将上述二维的数据将至一维（具体怎么实现见下文）。
二维数据降至一维：找到一条直线，将二维向量投影到该直线上，达到数据从二维(x1,x2)降至一维(z1)的目的。

将三维的数据降至二维：将三维向量投影到一个二维平面上，迫使所有的数据都落在同一个平面上，从而实现从三维(x1,x2,x3)将至二维(z1,z2)。

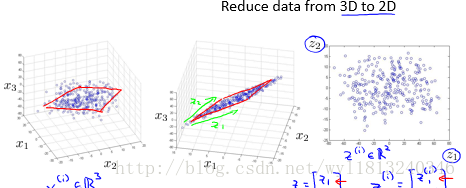
同样地，可以实现从任何维度的数据将至任何想要的维度。

降维的两个功能：
1. 数据的压缩。从上面例子中可以看出，明显对数据进行了压缩。
2. 数据的可视化。对于我们来说我们最多能够可视化一个三维的画面，但是有些数据的维度大于三维，使得我们没办法可视化，但是使用降维的办法可以实现将原来的数据将至三维、二维甚至一维，从而有助于可视化显示。但是降维之后产生新特征的意义就必须有我们自己去发现了。

主成分分析（Principal Component Analysis, PCA）:
PCA是最常见的降维算法。它的思想为：找到一个由一系列方向向量组成的低维平面，当我们把所有的数据投射到该低维平面时，我们希望投射平均均方误差尽可能地小。投射误差是从特征向量向该低维平面做垂线的长度。
下面我们以二维为例，来对概念进行形象化表示：

PCA方法的问题描述：
对于将n维数据降至k维来说，我们的目标就是找到向量$u^{1},u^{2},...,u^{k}$使得总的投射误差最小。

PCA算法的过程如下：
1. 均值归一化（特征的缩放）。需要计算出所有特征的均值，然后令$x_{j}=x_{j}-u_{j}$，同时如果特征是不同数量级上，我们还需要将其除以标准差。
2. 计算协方差矩阵$\Sigma$:

$$\Sigma =\frac{1}{m}\sum_{i=1}^{m}(x^{i})(x^{i})^{T}$$

3.计算协方差矩阵$\Sigma$的特征值：
在matlab中可以利用奇异值分解来求解，函数形式为：[U,S,V]=svd(sigma)，同时也可以使用eig(sigma)来求解，但是对于半正定矩阵的sigma来说，svd更加具有数据的稳定性。

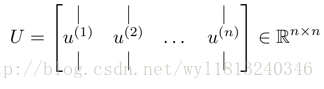
4. 获取符合要求的新的特征向量。
上式中的U就是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们想从n为将至k维，我们只需要从U中选取前k个向量，获得一个n*k的矩阵$U_{reduce}$，然后通过$U_{reduce}$获得符合要求的新的特征向量$z^{i}$:

$$z^{i}=U_{reduce}^{T}\times x^{(i)}$$

其中x是$n\times1$维的，所以求得的z是$k\times1$

怎样选择主成分的数量：
选择主成分分析有一个原则：希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的k值。其中平均均方误差的计算公式如下：

$$f=\frac{1}{m}\sum_{i=1}^{m}||x^{i}-x_{approx}^{i}||^{2}$$

训练集方差为：

$$g=\frac{1}{m}\sum_{i=1}^{m}||x^{i}||^{2}$$

它衡量了样本距离原点有多远。如果我们希望这个比例小于1%，这就意味着原来数据的方差有99%都保留了下来。
介绍完上述原则，我们来学习两种选取k值得的方式：
1. 先令k=1，然后进行PCA，分别计算出$U_{reduce},z^{(1)},z^{(2)},...,z^{(m)},x_{approx}^{(1)},x_{approx}^{(2)},...,x_{approx}^{(m)}$检查是否$\frac{f}{g}\leq 0.01$，如果满足则选择k=1，如果不满足，则令k=2，重复上述步骤，直到找到满足这个比例的k为止；
2. 还有一种更好的选择k值的方法：在我们求解协方差矩阵的特征值时，我们采用了[U,S,V]=svd(sigma)，其中S是一个$n\times n$的矩阵，只有对角线上有值，而其它位置均为0，我们可以利用这个矩阵来计算该比例：

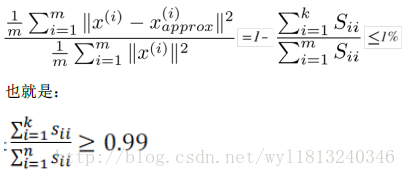
利用上述方法选出最小的符合要求的k值，在得到k值之后，重新计算出f/g的值。对于了解PCA的人来说，一般都是给出k值和平均均方误差与训练集方差的比值 ，才能给别人更好的解释你选择的k值是多么接近原始的数据。

重建原始数据：
在讲述上面的PCA算法时，我们都是将数据进行压缩，从一个高维的数据降维至低维的数据，那么我们能不能从压缩的数据重建出与原来高维数据类似的数据呢？
我们在来看一下数据降维的过程，当找到一个$U\in \mathbb{R}^{n\times n}$矩阵时，然后选择前k个向量组成一个新的矩阵$U_{reduce}\in\mathbb{R}^{n\times k}$，最后降维之后的新的特征向量$z=U_{reduce}^{T}*z$，这就是降维的过程。
而对于重建数据来说，我们仍然使用$U_{reduce}$进行重建，重建之后的特征向量的计算为：$x_{approx}=U_{reduce}*z$，基本上能够达到重建的目的，即$x_{approx}\approx x$
这种由低维数据Z回到为压缩的原始数据X的过程称之为重建原始数据。
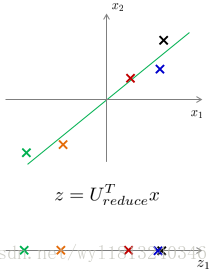
我们下面以一个二维到一维然后从一维到二维的过程为例简单理解一下：

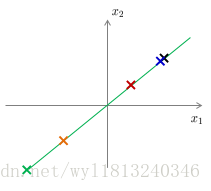
上面的左图是一个从二维降维至一维的过程，找到方向向量，然后将二维的数据向该方向向量作投影，得到一个一维的数据z；右图是一个反的过程，将一维的数据还原成二维的数据，还原结果如右图，从图上可以看出，还原后的数据会全部在方向向量上，会和原始的数据有一定的误差，但是误差不是很大，能够还原基本的数据结构。

主成分分析应用的建议：
假如我们对一张100*100的图像进行某个计算机视觉的机器学习，则我们总共有10000个特征，如果我们直接使用学习算法，速度可能非常慢，所以处理这个问题的过程如下：
1. 运用主成分分析将数据压缩至1000个特征
2. 然后对训练样本集运行学习算法（逻辑回归、svm、神经网络等）
3. 在预测时，采用之前学习而来的$U_{reduce}$将输入的特征x转化成特征向量z，然后进行预测。
伪代码：
输入：$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})$
提取非标签的数据：$x^{(1)},x^{(2)},...,x^{(m)}$，然后

$$x^{(1)},x^{(2)},...,x^{(m)}\in \mathbb{R}^{10000}\overset{PCA}{\rightarrow}z^{(1)},z^{(2)},...,z^{(m)}\in \mathbb{R}^{1000}$$

新的训练集：$(z^{(1)},y^{(1)}),(z^{(2)},y^{(2)}),...,(z^{(m)},y^{(m)})$，对于新的训练集运行学习算法（以逻辑回归为例）：

$$(z^{(1)},y^{(1)}),(z^{(2)},y^{(2)}),...,(z^{(m)},y^{(m)})\overset{algorithm}{\rightarrow}h_{\theta}(z)=\frac{1}{1+e^{-\theta^{T}z}}$$

对于一个测试样本x:

$$x\overset{PCA}{\rightarrow}z\rightarrow h_{\theta}(z)$$

值得注意的是：仅仅在训练集上执行PCA，对于交叉验证集和测试集均使用训练集中得到的$U_{reduce}$。

使用PCA的建议：
1. PCA不是缓解过拟合的方法，对于缓解过拟合仍然采用正则化的思想。原因在于主成分分析只是近似地丢弃掉一些特征，它不会考虑任何与结果变量有关的信息(因为PCA是一种无监督的方法，不会使用标签信息)，因此可能会丢失非常重要的特征。对于正则化来说，会考虑结果变量(充分使用标签信息)，不会丢掉重要的特征。
2. 不要默认的将PCA一定是学习算法的某一部分，应该首先使用原始数据集用于学习算法，当用原始数据集学习算法运行的很慢或者内存和硬盘占用很高时，在考虑使用PCA。

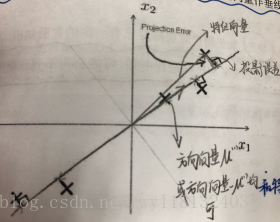
我们对PCA作投影时的投射误差和线性回归的误差作一个比较：
主成分分析最小化的是投射误差，而线性回归最小化的是预测误差。线性回归目的是预测结果，而主成分分析不作任何预测。

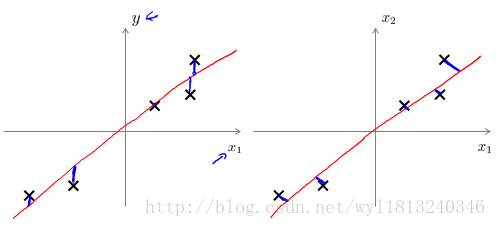
左图表示的是线性回归误差产生的过程(垂直于横轴投影)，右边是主成分分析投影误差产生的过程(垂直于红线的投影)。

PCA降维的优缺点：
优点：
1. 对数据进行降维处理。PCA根据协方差矩阵特征值的大小进行排序，根据需要取前面最重要的部分，将后面的维度省去，可以达到降维从而简化模型或是对数据进行压缩的效果，同时又最大程度的保持了原有数据的信息。
2. 完全无参数限制。完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后结果只与数据相关，与用户独立
缺点：
无参数限制同样也会成为它的缺点，如果用户通过观察得到了一些先验信息，掌握了数据的一些特征，但是无法通过参数化等方法进行干预，可能会得不到预期的效果。