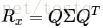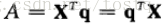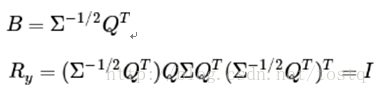【机器学习算法笔记】6. 降维与主分量分析（PCA）

6.1 PCA算法

特征选择问题是指将数据空间变换到特征空间，我们希望设计一种变换使得数据集由维数较少的有效特征来表示。
PCA是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。
通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。
假设降维后的向量由m维降为l维，这里的Q指数据空间的基：
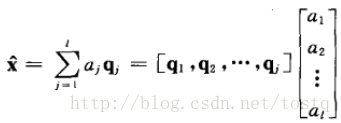
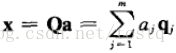
这里写图片描述

降维后的误差，由于数据的各基都正交的，所以误差与降维数据也是正交：

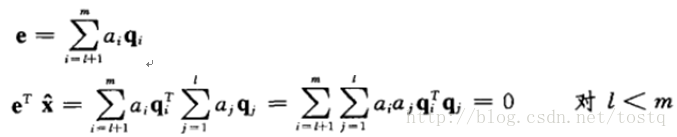
如果X的均值为0：
X在数据空间投影的方差为：

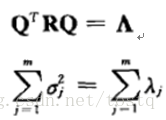
所以降维要选择方差最大的项，即特征值最大的项，而抛弃方差较少的项

6.2 核PCA方法

核方法主要是在普通PCA方法中，将相关矩阵更改为如下形式：
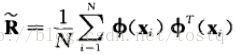
这里写图片描述
同理，也要保证均值为零（只有均值为零，才能保证方差与特征值相等）

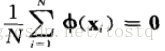
求解方法也是类似的：

6.3 信号预白化

我们已经了解了如何使用PCA降低数据维度。
在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化。举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。
白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：（1）特征之间相关性较低；（2）所有特征具有相同的方差。
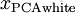
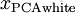
我们说，这里写图片描述是数据经过PCA白化后的版本:
中不同的特征之间不相关并且具有单位方差。

6.3.1 白化的具体步骤

1、输入数据0均值化
2、利用PCA降维，消除相关性
如果你想要得到经过白化后的数据，并且比初始输入维数更低,可以仅保留中前k个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论)，中最后的少量成分将总是接近于0，因而舍弃这些成分不会带来很大的问题。

通过Q变换将x变成多个不相关量：
3、方差化为1
建立一线性变换，得到不相关输出：

6.4 K-L算法

K-L变换与PCA变换是不同的概念，PCA的变换矩阵是协方差矩阵，K-L变换的变换矩阵可以有很多种（二阶矩阵、协方差矩阵、总类内离散度矩阵等等）。当K-L变换矩阵为协方差矩阵时，等同于PCA。

6.5 降维方法

6.5.1 Lasso方法

Lasso方法是一种压缩估计，它通过构造一个罚函数得到一个较为精炼的模型，使得它压缩一些系数，同时设定一些系数为零。因此保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。Lasso 的基本思想是在回归系数的绝对值之和小于一个常数的约束条件下，使残差平方和最小化，从而能够产生某些严格等于 0 的回归系数，得到可以解释的模型。lasso通过参数缩减达到降维的目的；
Lasso方法类似于最小二乘法，只是将最小二乘法的正则项由L2变成L1范式：
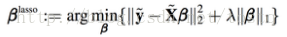
这里写图片描述
遗憾的是，lasso是不能像ridge regression和linear regression一样写出“显式解”的，必须用数值方法去近似上面的优化问题的解。但lasso算出来的权重参数β的很多项是0。
因为lasso选了1-norm，导致theta-lasso的范围“有棱有角”，在和normal equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话，就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
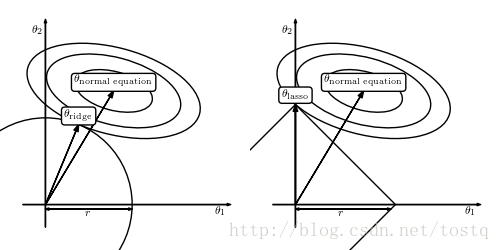
这里写图片描述
因为lasso选了1-norm，导致theta-lasso的范围“有棱有角”，在和normal equation“相互妥协”的过程中万一碰到了“楞”或者“角”的话，就会有一个解释变量的参数变成0。比如右图中的theta1就变成了0。而左图是无论如何不可能让某个参数变成0的。
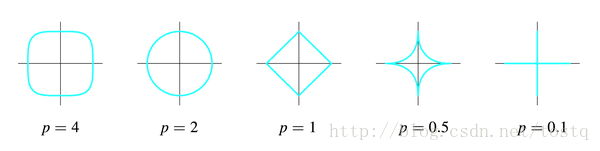
当p小于1时刚才那幅图里的圆形和正方形会继续“往里陷”，变成下面的样子：这样这个集合就不是凸集了，也没有办法做最优化了。
这里写图片描述
实际上，线性回归的本质，是把一个n维空间的向量Y投射到p+1维空间，这个p+1维空间就是p个X解释变量和一个常数向量，这p+1个向量span出来的一个“亚空间”。当Y本身在n维空间太复杂了，将n维空间的Y投射到p+1维空间，尽可能的去获得更多的Y的信息。然而有些时候由于数据本身的问题，p+1维空间发生了“退化”或者“坍塌”，为了“支撑”起这个空间，需要在对角线上都加了一个常数，即为正则化思想。
当投射到p+1维空间时，可以直接在n维空间找到Y的全部信息，也就是所谓的解线性方程组(p+1=n)。

6.5.2 线性判别法LDA

线性判别法即LDA通过找到一个空间使得类内距离最小类间距离最大所以可以看做是降维。线性判别式分析，又称为Fisher线性判别~（Linear discriminant analysis）(Fisher linear discriminant)，LDA是有监督的方式，它先对训练数据进行降维，然后找出一个线性判别函数。
两个类的均值向量：
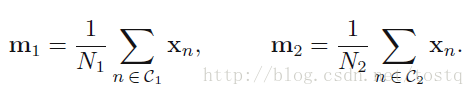
这里写图片描述
对样本进行投影时，使得类别最简单的分离（这里的分类是线性分类，w是分类权重，y=wTx），是投影的类别均值的分离：
最大化类间均值

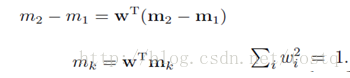
最小化类内方差

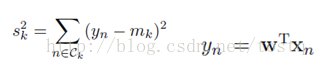
1. Fisher 判别准则：

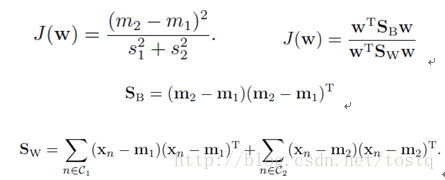
对权重W求微分，使得J(W)最大化，当：
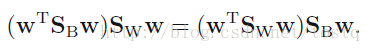
这里写图片描述
化简之：

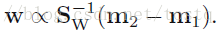
2. 多类线性判别分析：
假设有C个类别，降以一维已经不能满足分类要求了，我们需要k个基向量来做投影，W=[w1|w2|…|wk] 。样本点在这k维投影后的结果为[y1,y2,…,yk]，且有

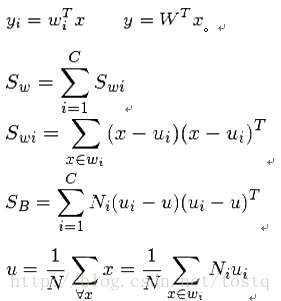
同样是求一个类似于(1)式的最优化问题，我们得到
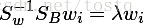
这里写图片描述