机器学习第二周（上）

一、线性回归

1、多元线性回归

1.1、训练集

面积	卧室数量	层数	年份	价格
2104	5	1	45	460
1416	3	2	40	232
1534	3	2	30	315
852	2	1	36	178

其中，
$n=4$表示特征(面积\ 卧室数量 \ 层数 \ 年份)组数量。
$x^{(i)}$表示第 $i$个样本。
$x^{(i)}_j$表示第 $i$个样本的第 $j$个特征。

1.2、假设函数

假设训练集中的特征贴合以下函数：
$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n$

上述假设函数也可以用矩阵乘法表示，先令 $x_0=1$，则输入变量 $x$和模型参数 $\theta$可表示为：
$\overrightarrow{x}= \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{bmatrix} \quad \overrightarrow{\theta}= \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \\ \vdots \\ \theta_n \\ \end{bmatrix}$
依据上式，有
$\quad h_\theta(x)=\theta^Tx$

1.3、代价函数

根据上面提到的向量 $\overrightarrow{\theta}$，代价函数为：
$J(\overrightarrow{\theta})=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))^2$

据上式，模型参数的迭代公式（梯度下降）为：
$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\overrightarrow{\theta})\quad(for\quad every\quad j)$
将代价函数代入上式，可得：
$\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))(x^{(i)}_j)\quad(for\quad every\quad j)$
PS： $x^{(i)}_0=1；j为0至n$

2、特征缩放和均值归一化

2.1、背景

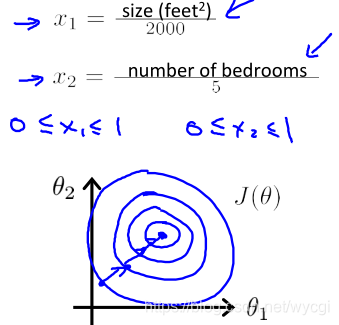
如果输入变量 $x$的数值范围较大，那么代价函数的轮廓图变得细长，梯度下降过程曲折费时，如下所示：

如果样本中的特征 $x$的数值范围合理，那么代价函数的轮廓图变圆，梯度下降顺畅，如下所示：

2.2、具体实现

1. 特征缩放
   通过调整每个特征的比例： $\frac{x^{(i)}_j}{x^{(i)}_{max}-x^{(i)}_{min}}$，其中分母是指各特征的最大值减最小值，使样本中的特征 $x$在【-1，1】范围附近，太小如【-0.0001,0.0001】或太大如【-100,100都不可以】。
2. 均值归一化
   通过 $\frac{x^{(i)}_j-\mu_i}{s_i}$代替 $x^{(i)}_j$，使样本中的特征 $x$在【-0.5，0.5】范围附近。

3、选择学习速率 $\alpha$

1. 如果学习速率选择合适，则代价函数在迭代过程中的取值曲线图如下：
   

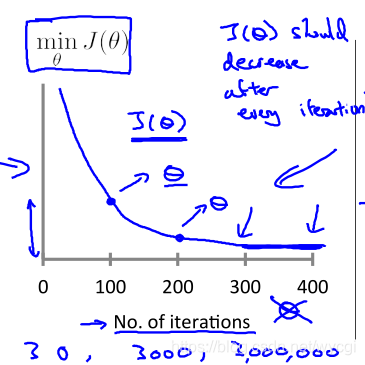
PS：可以在进行自动收敛测试时，设定迭代在下降值小于 $10^{-3}$时，则声明收敛，结束迭代。

2. $\alpha$过小，则曲线图下降缓慢，如下：
   

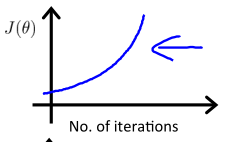
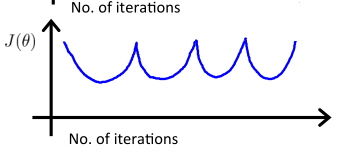
3. $\alpha$过大，则曲线图可能来回波动甚至一直上升，如下：
   

4. 具体实践中，可以取0.001、0.01、0.1和1等不同数量级的数进行尝试。

4、慎重选择特征

现有长和宽两组特征的样本e，但是任务T是根据面积预测价格，所以应该将长和宽两组特征组合（长×宽=面积），得到面积，再将得到的面积作为新特征，组成新的样本进行回归。

5、合理选择模型（假设函数）

如下图，因为随着面积的增大，价格是不会降低的，所以选择下方的多项式回归模型可能更加贴切：

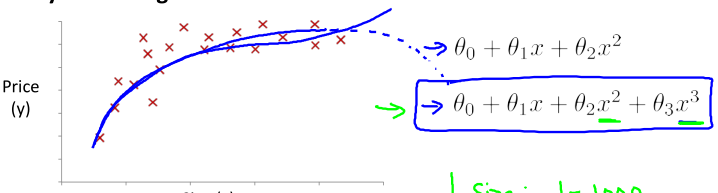
同时，下方的模型也可以表示为线性：
$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n\quad x_n =(size)^n$

除此以外，还可以使用下面的模型：
$h_\theta(x)=\theta_0+\theta_1(size)+\theta_2\sqrt{(size)}$

6、正规方程法

6.1、用途

与梯度下降算法目的相同，均是求得模型参数 $\theta$。

6.2、求解思路

基于微积分，令代价函数的各个偏导数为0，直接求出极值点
$\alpha\frac{\partial}{\partial\theta_j}J(\theta)=0 \quad (for \quad every \quad j)$
但是，当特征较多时，上面的计算极为复杂，在具体实践中，多数采用如下过程进行求解：

$x_0$	面积	卧室数量	层数	年份	价格
1	2104	5	1	45	460
1	1416	3	2	40	232
1	1534	3	2	30	315
1	852	2	1	36	178

1. 设计矩阵 $X$
   由各样本 $x^{(i)}$转置组合得到，其中 $x^{(i)}_0=1$
   $X= \begin{bmatrix} 1 & 2104 & 5 & 1 & 45 \\ 1 & 1416 & 3 & 2 & 40 \\ 1 & 1534 & 3 & 2 & 30 \\ 1 & 852 & 2 & 1 & 36 \end{bmatrix} \quad \overrightarrow{y}= \begin{bmatrix} 460 \\ 232 \\ 315 \\ 178 \end{bmatrix}$
2. 模型参数向量 $\overrightarrow{\theta}$
   $\overrightarrow{\theta}=(X^TX)^{-1}X^T\overrightarrow{y}$
   上式推导如下：
   $X\overrightarrow{\theta}=\overrightarrow{y}\rArr X^{-1}X\overrightarrow{\theta}=X^{-1}\overrightarrow{y}\rArr \overrightarrow{\theta}=X^{-1}((X^{-1})^TX^T)\overrightarrow{y}\rArr \overrightarrow{\theta}=(X^TX)^{-1}X^T\overrightarrow{y}$

6.3、与梯度下降相比较

梯度下降	正规方程
需要迭代多次	不需要迭代
需要选择合适的 $\alpha$	不需要选择参数
计算量小，在样本中特征组数量过多时（ $n \gt 10000$）也能较好运行	计算量大， $0(n^3)$，在样本中特征组数量较少（ $n \lt 10000$）才能较好运行

6.4、潜在的不可逆性

如果 $X^TX$不可逆，则无法求解模型参数向量，解决方法有：

1. 去掉多余的特征组，比如一个特征组是关于平方米，另一个是平方厘米，则取其中一个即可。
2. 如m=10，n=100，特征太多，删除一些不必要的特征或者正则化（下篇文章中学习）
3. 用octave中pinv()命令，求伪逆矩阵（其求解思路可见上一篇博文《机器学习第一周》）