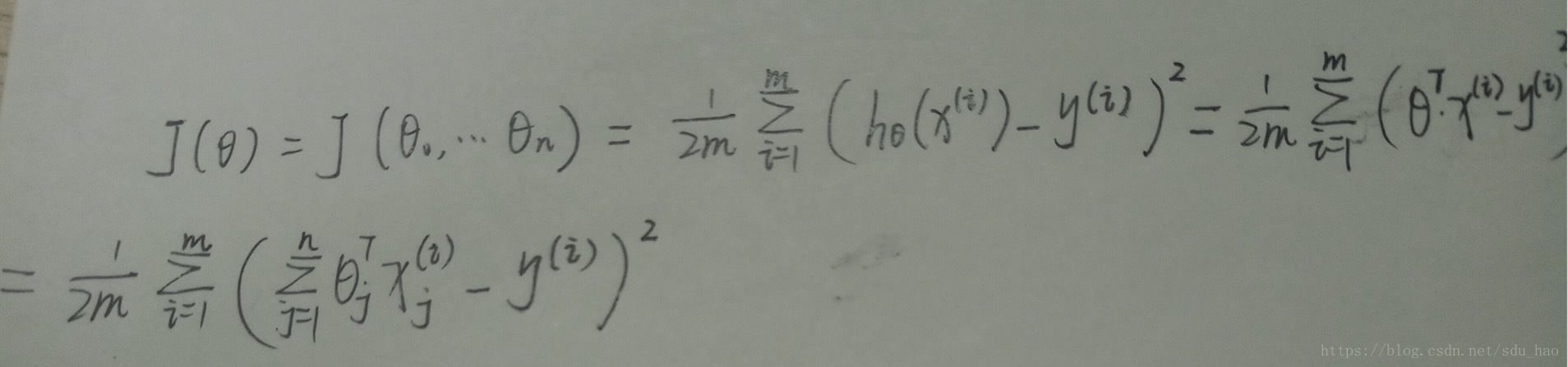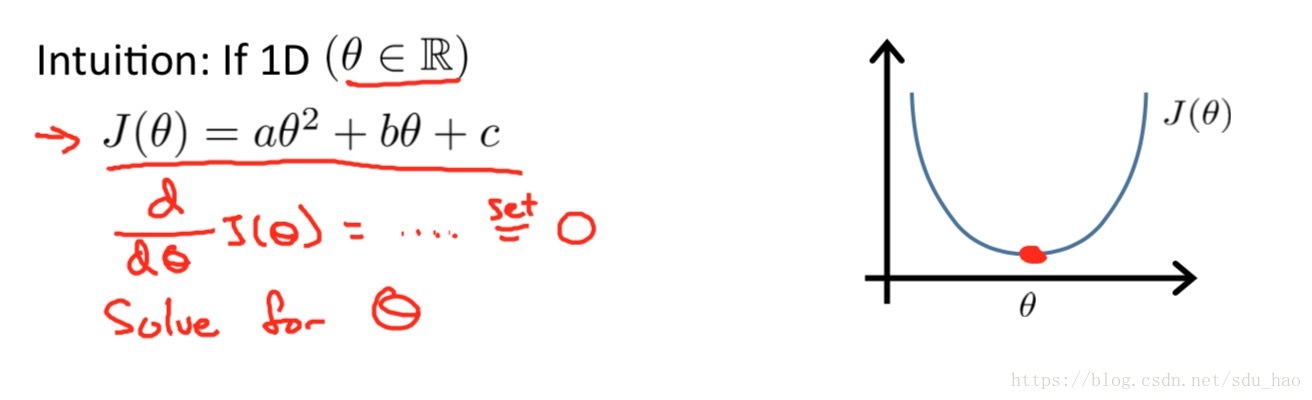课程视频链接:https://www.coursera.org/learn/machine-learning/home/welcome
第二周PPT汇总下载链接:https://pan.baidu.com/s/1CfhGOP6JG8M4JBSPB9NM-Q 密码:7c1r
上一篇博客主要介绍了第一周的课程的内容,总体来说比较简单,包括机器学习简介、并以引入单变量线性回归来讲解代价函数和模型的表示以及如何利用梯度下降法来求解单变量线性回归(重点);本篇博客将系统的介绍第二周的内容,其实是对第一周内容的扩展和延伸,把使用场景更一般化,从单变量线性回归演变到多变量线性回归,并通过实例来介绍使用梯度下降法求解多变量线性回归的实用技巧,模型特征选择与特征缩放以及最后引入一种线性回归的解析解法并与梯度下降法进行比较。从本周开始,将会有编程作业,后续还会进一步完善补充。接下来开始详细介绍本周内容。
目录
1.多元线性回归的引入
在上周的课程中,我们以房价数据集(仅包含面积一个输入变量)为例,介绍了单元线性回归的相关知识。我们首先回顾一个上周的内容。
(1)单元线性回归
- 数据集
该数据集输入变量仅有面积一个特征,输出变量是对应的房价。
- 假设函数
由于只有一个特征,所以假设函数只有两个待定参数。
(2)多元线性回归
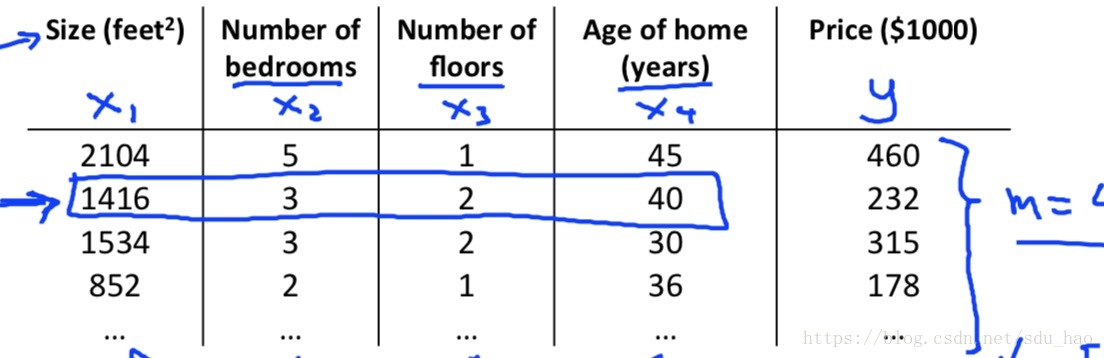
实际情况并没有这么简单,影响房价的因素还有很多,除了面积之外,比如还有卧室的数量,房子的层数以及房子的寿命等等一些因素。就此我们引入一个新的房价数据集。
- 数据集
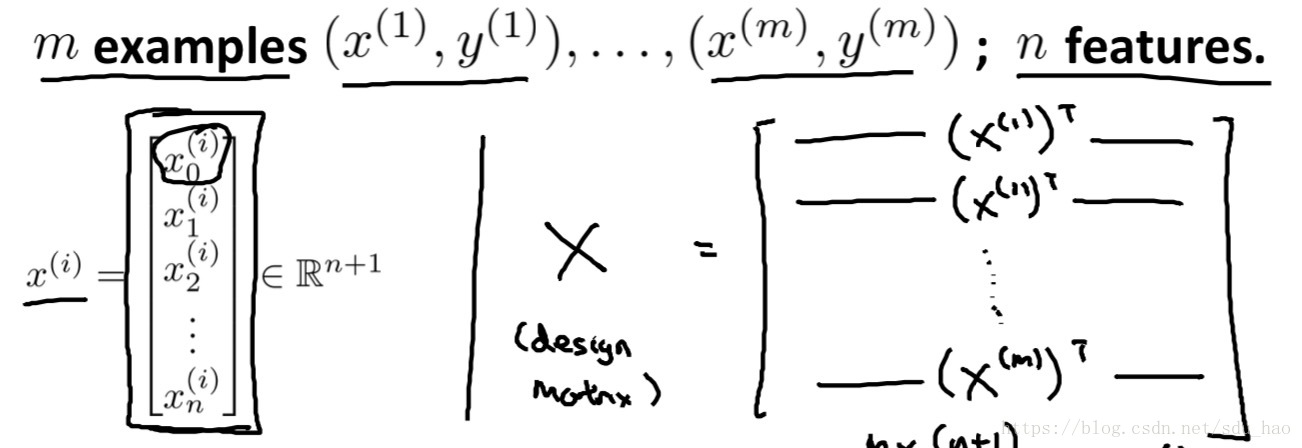
该数据集的输入变量包含四个特征,输出变量是房价,二者构成了训练样本。我们引入一些新的模型表示符号:
| 模型表示符号 | 含义 |
| 训练集中的训练样本数量 | |
| 输入变量的特征数量 | |
| 输入变量 | |
| 输出变量 | |
| 模型参数 | |
| 训练集中的训练样本 | |
| 训练集中的第 |
|
| 第 |
|
| 第 |
举例来说,就上图的数据集而言,,
即第2个训练样本的第三个特征值。
- 假设函数
现在我们给出该实例的假设函数,由于它有四个输入特征,所以其假设函数应该有5个参数。
为了方便表示,我们定义,推广到一般化的多元线性回归,如下所示:
其中:
输入变量和参数
均为
的向量。
2.使用梯度下降法求解多元线性回归
多元线性回归的一般形式
输入变量和参数
均为
的向量,均有
个分量。
其中代价函数也可以写成如下形式:
对比单元线性回归和多元线性回归使用梯度下降法的迭代过程:
左边为单元线性回归的参数更新过程,右边为多元线性回归的参数更新过程。这里仍然要注意在一次迭代所有的参数都务必是同时更新(具体可见第一周笔记)。可以发现二者的通式本质上是一致的,单元线性回归只是多元线性回归的特殊情况。
3.梯度下降法实用技巧
(1)特征缩放
- 如果你有一个机器学习的问题,该问题有多个特征,若能保证这些特征都处在一个相近的范围(即保证不同特征的取值在相近的范围内,这种情况下梯度下降法的收敛速度会很快。
- 几何解释:
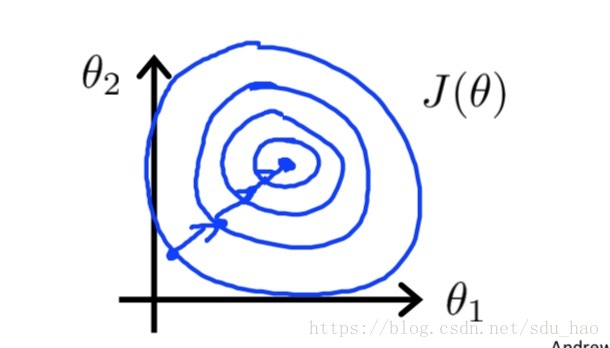
假设现在的输入变量有两个特征,为房子的面积,其取值范围为0-2000
;
为房子的卧室数量,其取值范围为0-5(间)。可见两个特征的取值范围相差甚远,现在我们做出代价函数
随参数
,
(此处忽略参数
)变化的轮廓线。
由于两个特征取值范围相差很大,此时的轮廓线大致如上图所示。会非常瘦长,且使用梯度下降法收敛到代价函数全局最小值时,会非常缓慢且出现波动的状况。
- 解决方案:
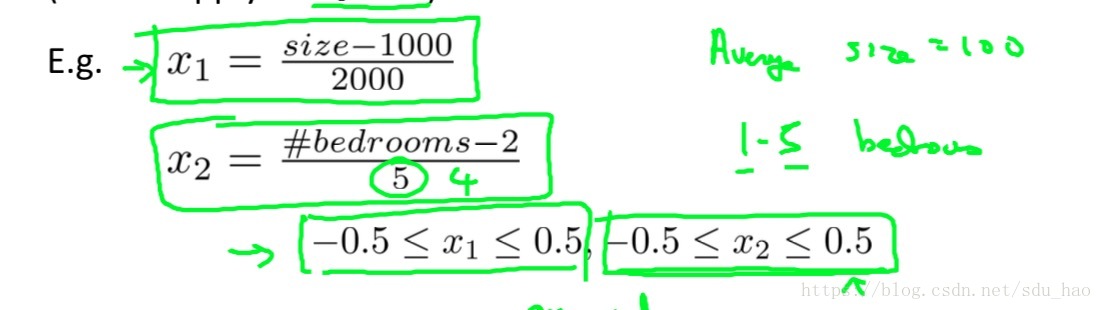
可以采用平均值归一化对特征进行缩放,公式如下:
其中为输入变量第
个特征,
为输入变量第
个特征所有取值的平均值,
为输入变量第
个特征的取值范围(最大取值减去最小取值),注意
,第0个特征是我们为了方便表示自己添加的,默认取值为1,不用归一化。那么用平均值归一化对上例中的特征进行归一化可得:
可以发现所有特征的取值范围在归一化后,都会在一个相同或相近的范围内。此时,我们再画出代价函数随参数
,
(此处忽略参数
)变化的轮廓线,可能就如下图所示:
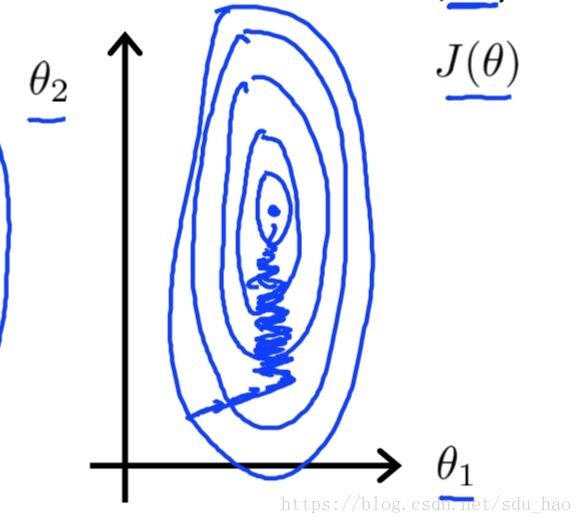
此时的轮廓线会比较正和圆,这种情况下,梯度下降法收敛速度会很快,循环迭代次数更少。
- 总结:当使用梯度下降法解决多元线性回归时,为了使算法收敛更快,务必要对特征进行归一化,使其取值在一个相同或者相近的范围内,尤其是各个特征取值范围差异巨大的情况下,归一化就显得尤为重要了。
(2)学习率
- 两种判断梯度下降法是否收敛的方法
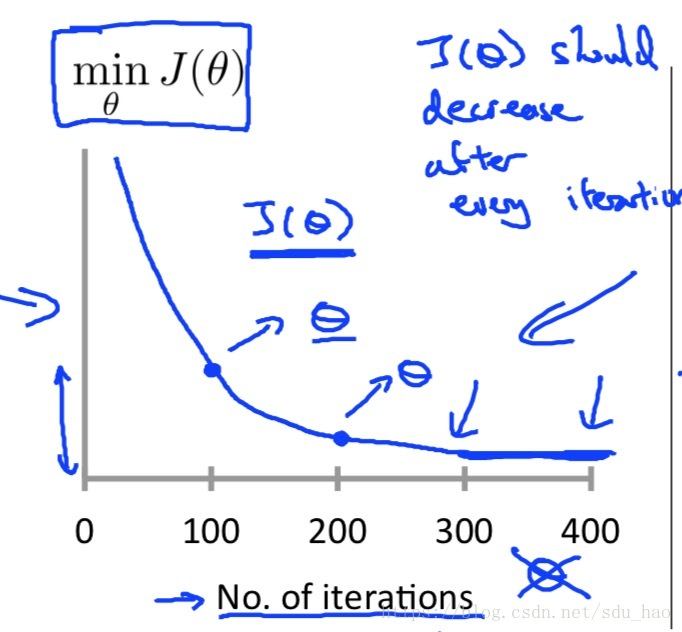
1.做出代价函数随参数更新迭代次数的变化曲线
上图的横坐标为迭代次数,当迭代到某个次数时,如100次,此时会得到一个新的参数,将这个新参数代入代价函数
所得的数值即为该点的纵坐标。每到一个新的迭代次数,都会得到一个新的参数
,对应也会得到一个
,从而绘制出上图曲线。
如果梯度下降法正常工作的话,每次迭代后,代价函数都会下降。
这条曲线作用就是判断梯度下降法是否收敛,如上图所示,当迭代次数超过300次,在300-400之间时,我们会发现曲线比较平坦,也就是说此时并未下降多少,那么说明此时梯度下降法基本收敛。
2.自动收敛测试
若在某次迭代后,代价函数的变化范围小于某个阈值
,
是一个很小的值,一般取
,则认为梯度下降法基本收敛。
- 上述两种方法的比较
实际上多用方法1,而不是方法2.
1.首先方法2很难确定一个合适的阈值。
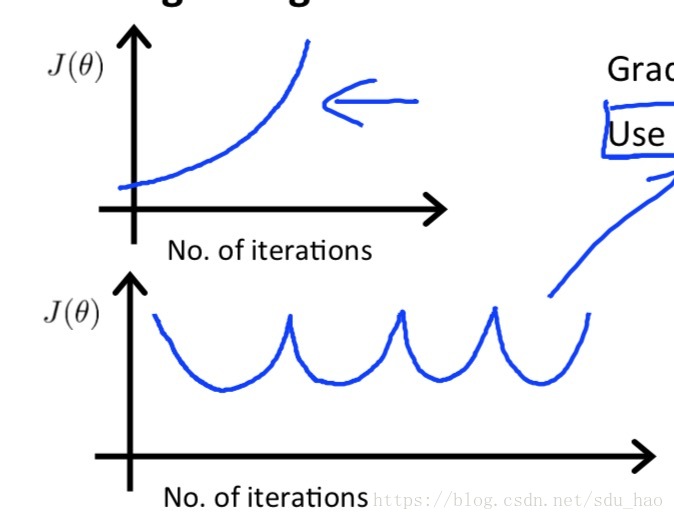
2.方法1不仅能够判断梯度下降法是否收敛,而且还能在梯度下降法不正常工作时,提前警告你,比如下图的情况:
如果出现上图中的两种曲线,说明梯度下降法没有正常工作,此时应该选择一个小的学习率。
- 学习率
的选择
我们在上一周的课程中曾经讨论过这个问题。
1.对于足够小的学习率,
会在每次迭代后下降。
2.但是如果学习率过小,梯度下降法收敛会非常缓慢。
3.当学习率过大时,
或许不会在每次迭代后下降,甚至不会收敛。
4.实际过程中,我们可以根据随迭代次数变化的曲线,来选择一个合适的
。
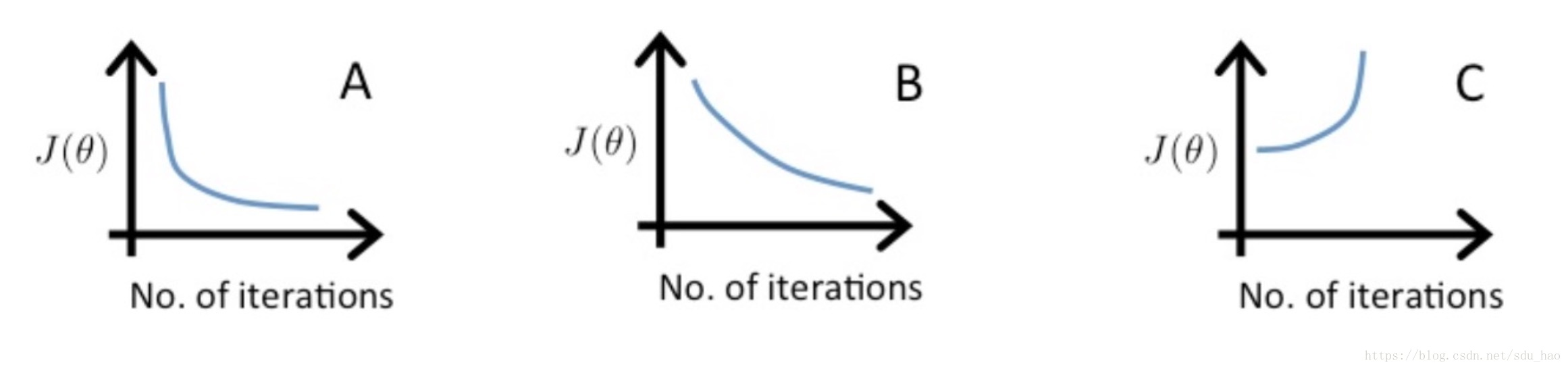
比如C图中,随迭代次数上升,说明
设置的比较大,此时应减小
;B图中,
虽然随迭代次数下降,但下降的比较缓慢,说明
设置的比较小,此时应增大
;A图中的
应该介于B和C之间,比较合适。
5.学习率的选择可以依次进行。
4.特征和多项式回归
(1)创造新特征
有时在拿到训练样本时,我们不一定要使用所有原始特征,可以对原始特征进行一定的处理,创造出一个新的特征,比如:
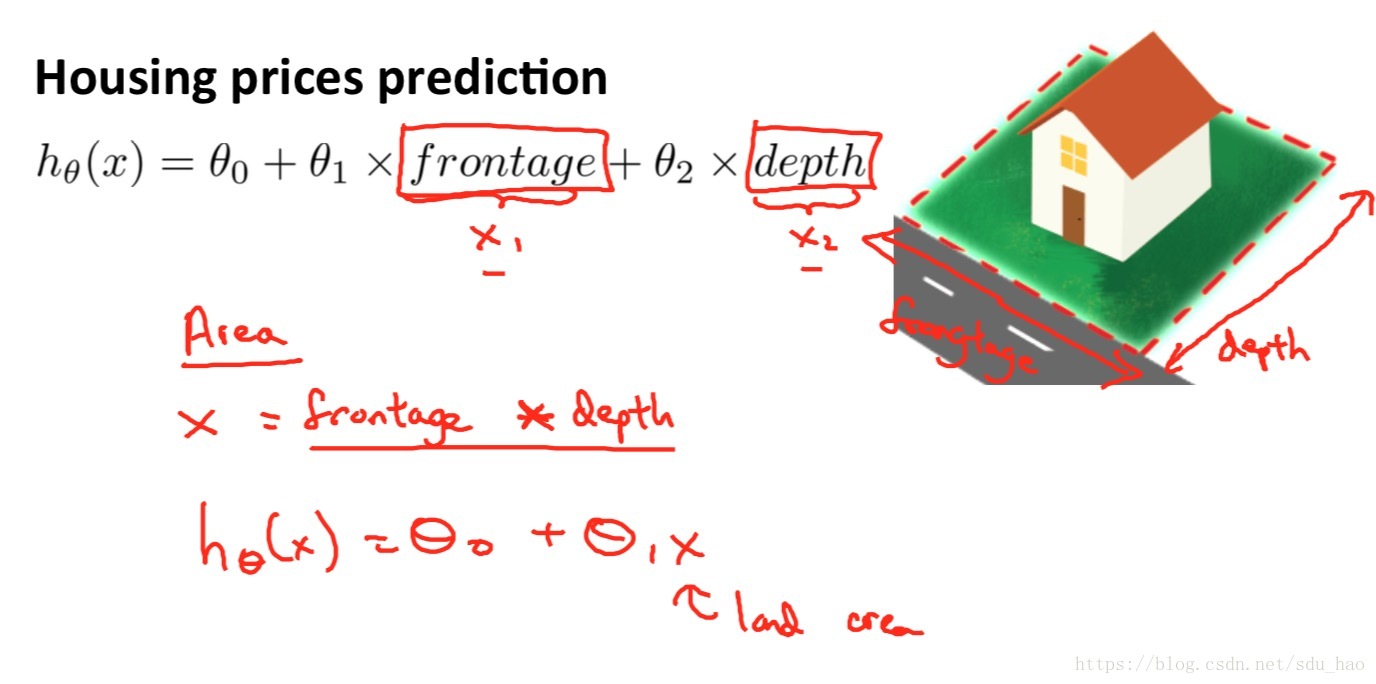
输入变量有frontage和depth两个特征,其中frontage是房子的沿路宽度,depth是房子的纵深;由于房子的面积可以表示为二者相乘,那么此时我们可以创造出一个新特征面积来代替原始的特征,或许算法效果会更好。
(2)多项式回归
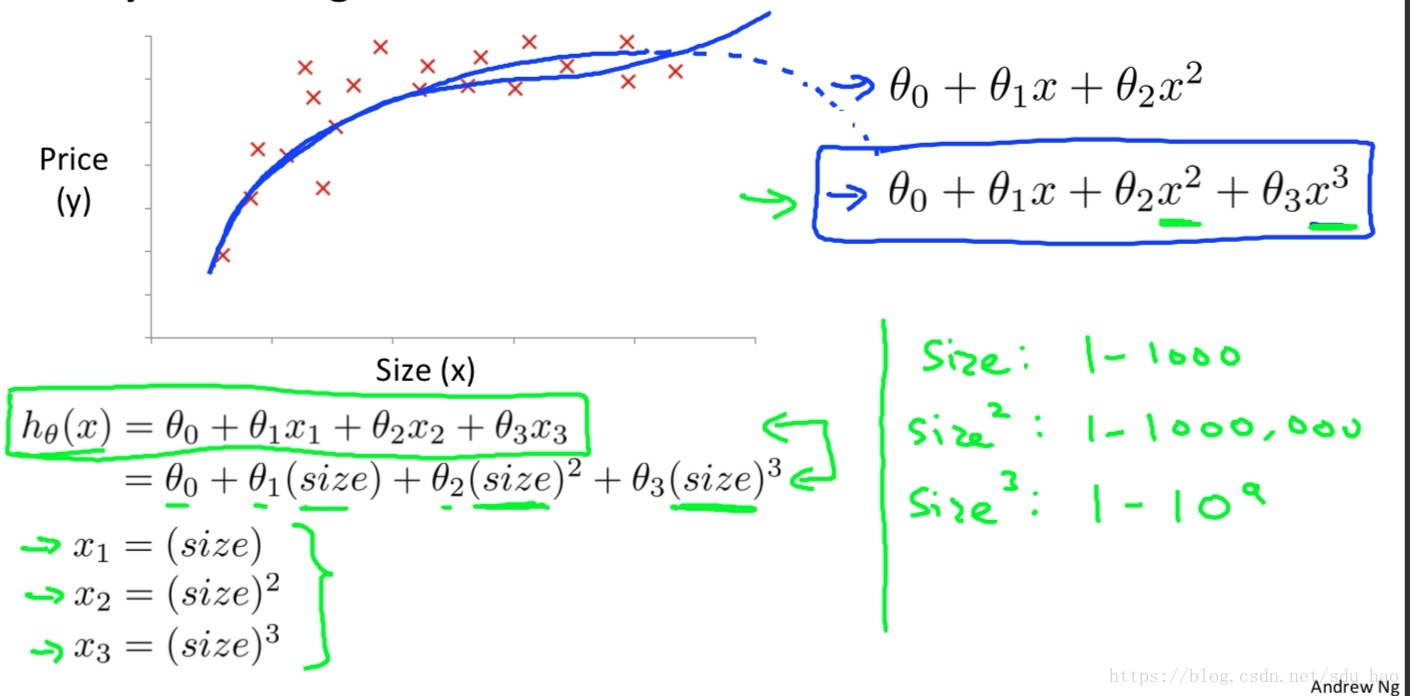
仍然是预测房价问题,此时输入变量只有面积这一个特征,我们绘制出房价和面积的散点图如上所示。之前我们一直用线性函数来拟合,其实我们也可以尝试用曲线来拟合。比如我们可以采用二次或者三次多项式来拟合。
以三次多项式拟合为例,其假设函数如上所示,此时会出现面积的平方和立方;这时我们可以构造两个新的特征
使其分别等于面积的平方和立方,那么就构成了一个新的多元线性回归,依然可以用梯度下降法求解参数。但此时一定要注意特征的归一化,因为三个特征的取值范围差异很大(两个新特征分别是原始特征的平方和立方)。
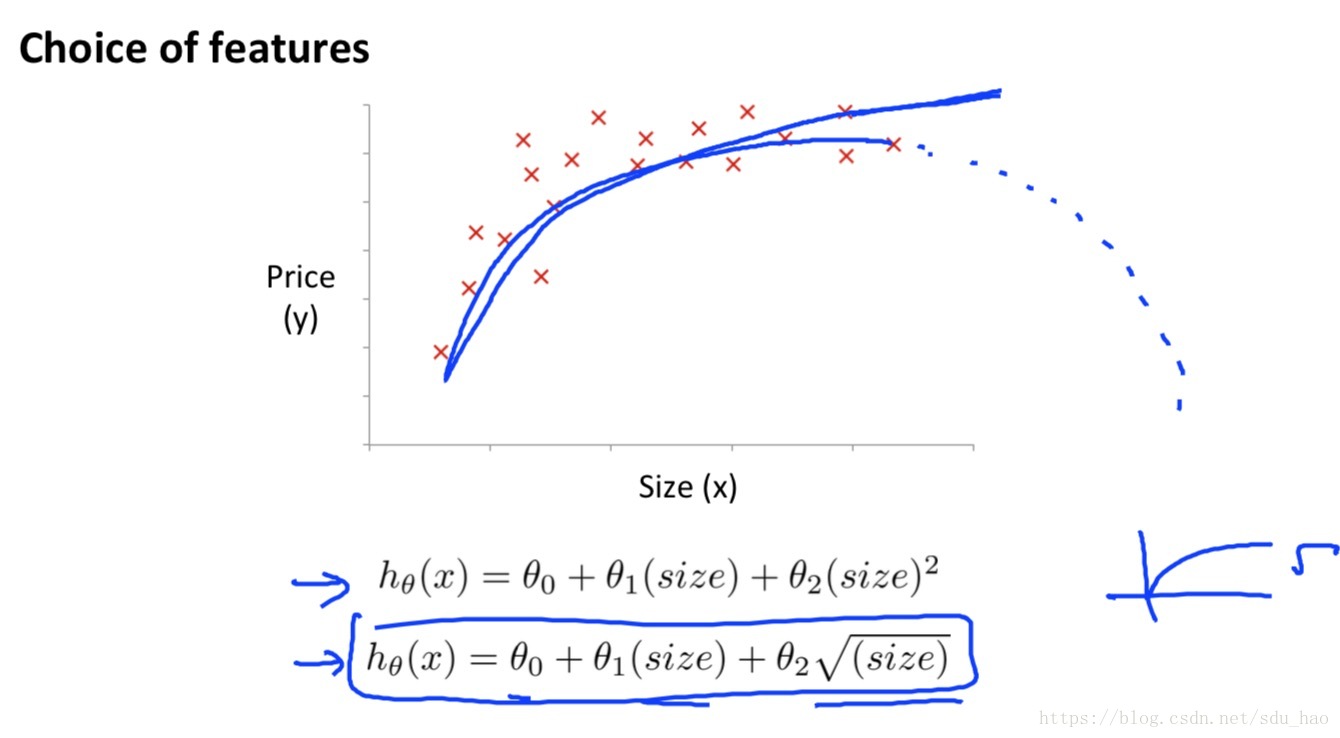
当然我们以可以用其他多项式拟合,道理都是一致的:
5.正规方程
(1)简介
之前我们在求解线性回归参数时,都是使用的梯度下降法;但是对于线性回归问题,还有一种求参数的解析解法--正规方程法,他可以直接一步到位的求解出线性回归的最优参数取值。
考虑如下所示的代价函数:
利用我们学过的微积分知识,我们知道如果求一个是的
最小,很显然的一种做法是将
对
求导并使导数值为零,解出的
即为所求。
(2)利用正规方程求解多元线性回归
实际中使用正规方程求解多元线性回归时,会有所差别,考虑下面的例子:
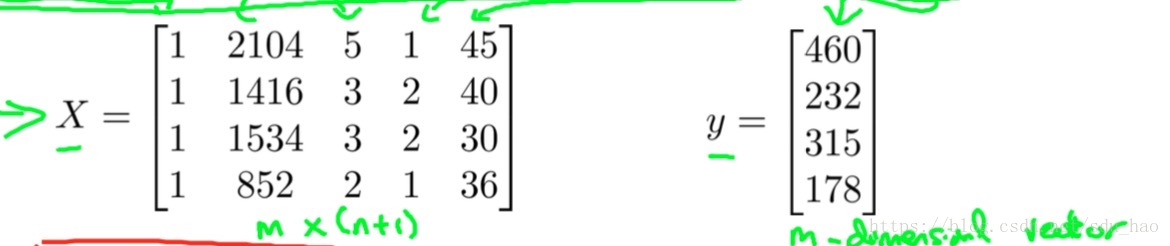
这仍然是之前使用的多特征房价数据集,在用正规方程之前,我们首先要增加一列特征,其值全部为1,然后构建一个矩阵
和一个向量
,
的每一行对应一个输入变量,
为输出变量构成的向量,如下所示:
那么此时模型的参数可有以下公式来求:
扩展到一般情况:
(3)梯度下降法与正规方程法比较
此比较是针对线性回归问题而言,梯度下降法不仅适用于线性回归也适用于其他机器学习算法;而正规方程法一般仅适用于线性回归问题。
梯度下降法:
优点:
- 当特征数量
非常大时,仍然适用,比较通用,一般当
大于几万时,使用梯度下降法更好。
缺点:
- 需要选择一个合适的学习率
- 需要很多次循环迭代来更新参数
- 当各个特征取值范围差异较大时,需要归一化,以加快收敛速度
正规方程法:
优点:
- 不需要选择一个合适的学习率
- 不需要迭代
- 不需要归一化特征
缺点:
- 需要计算
,
是一个
的方阵,计算其逆矩阵的复杂度大约是
,也就是说当
非常大时,求解速度会非常慢,一般适用于
小于1万的情况。
(4)正规方程的可逆性
之前我们也提到了,使用正规方程求解线性回归问题时需要计算,那么
如果不可逆,即是奇异矩阵怎么办?
不可逆的原因大致有以下两种:
1.存在冗余特征,也就是不同特征间线性相关(即不同特征存在线性关系,比如两个特征都表示面积,一个使用平方米为单位,另一个使用平方分米为单数,我们知道二者存在100的倍数关系)。根据线性代数的知识,若矩阵中的列向量线性相关,则矩阵不可逆。此时可以删除一个线性相关特征。
2.特征太多而训练样本比较少,即。此时可以删除一些特征或者使用正则化(今后的课程会讲)