1.导数(Derivative)的定义
在说次梯度之前,需要先简单介绍一下导数的概念与定义。导数(英语:Derivative)是微积分学中重要的基础概念。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
对于一般的函数f(x)f(x),其导数为:
f′(x)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx
如果不使用增量,f(x)f(x)在 x0x0处的导数 也可以定义为:当定义域内的变量 xx趋近于 x0x0时,
f′(x)=f(x)−f(x0)x−x0
2.次导数(subderivative)
次导数(subderivative)、次微分(subdifferential)、次切线(subtangent lines)和次梯度(subgradient)的概念出现在凸分析,也就是凸函数的研究中。
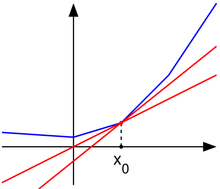
设f:I→R是一个实变量凸函数,定义在实数轴上的开区间内。这种函数不一定是处处可导的,例如最经典的例子就是f(x)=|x|,在x=0处不可导。但是,从下图的可以看出,对于定义域内的任何x0,我们总可以作出一条直线,它通过点(x0,f(x0)),并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数。
3.次导数与次微分(subdifferential)计算方式
凸函数f:I→R在点x0的次导数,是实数c使得:
f(x)−f(x0)≥c(x−x0)
对于所有I内的x。我们可以证明,在点x0的次导数的集合是一个非空闭区间[a, b],其中a和b是单侧极限
a=limx→x−0f(x)−f(x0)x−x0
b=limx→x+0f(x)−f(x0)x−x0
它们一定存在,且满足a ≤ b。
所有次导数的集合[a,b]称为函数ff在x0的次微分。
例如:考虑凸函数f(x)=|x|f(x)=|x|。在原点的次微分是区间[−1, 1]。x0<0时,次微分是单元素集合{-1},而x0>0,则是单元素集合{1}。
4.性质及推广
1.凸函数f:I→R在x0可导,当且仅当次微分只由一个点组成,这个点就是函数在x0x0的导数。
2.点x0x0是凸函数f的最小值,当且仅当次微分中包含零,也就是说,在上面的图中,我们可以作一条水平的“次切线”。这个性质是“可导函数在极小值的导数是零”的事实的推广。
5.次梯度
次导数和次微分的概念可以推广到多元函数。如果f:U→ R是一个实变量凸函数,定义在欧几里得空间Rn内的凸集,则该空间内的向量v称为函数在点x0的次梯度,如果对于所有U内的x,都有:
f(x)−f(x0)≥v⋅(x−x0)
所有次梯度的集合称为次微分,记为∂f(x0)。次微分总是非空的凸紧集。