导数
导数是一个很熟悉也很容易想象到的概念,导数体现了函数在某点的瞬时变化率,也可表示切线斜率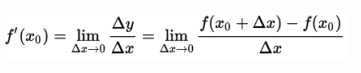
高中时我们对y=x^2求导的时候,实际上将其看作了一元函数,而y=f(x)是方程而不是函数,真正的函数是F(x,y)=x^-y,是一个曲面,只不过取了F(x,y)=0时候的特例。
偏导数
在二元函数F(x,y)中由于有两个自变量,导数也有x和y两个方向的分量,所以引入了偏导数。曲面上一点的瞬时变化率可以是任意方向(如果该点有导数),而高中时求的偏导数就是指多元函数沿坐标轴的变化率。
方向导数
在一元函数中,变化的方向只是一维的,如F(x)=x^2,x的变化方向只有变大和变小两个方向。而在多元函数中,如果我们要考虑在任意方向上的变化率,方向导数就是我们需要的。
设在二元函数F(x,y)中,是一个单位向量,它可以表示任意方向,
=
是f沿着u方向的方向导数,其实就是把沿u方向的微小变动分解到x和y方向上。方向导数还可表示成如下形式:
有了方向导数的形式,自然会想知道F(x,y)在哪个方向上的变化率最大,即max()
上式可写成,其中
,A向量就是求得的偏导数,所以当点确定时该向量也就确定了,而I在不断变化,当cosa=1,即a=0时最大,这时向量I与A平行,所以A向量就是梯度,梯度也就理所当然的表示函数变化率最大的方向了,所以梯度的方向就是函数增大最快的方向。
扫描二维码关注公众号,回复:
2407684 查看本文章

