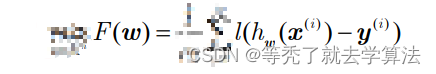搜索算法笔记

机器学习中的搜索算法

机器学习中的搜索算法

本节知识导图

预先需要了解：

凸函数优化：局部最优解一定是全局最优解

凸函数：由上图来看，凸函数的几何意义在于，定义域中任意两点连线组成的线段都在这两点的函数曲线（面）上方。

非凸函数优化：局部最优解不一定是全局最优解

梯度下降算法

算法思想

从线性回归问题了解算法思想：

从线性回归博文中，得知线性回归的任务就是确定唯一的 $w^*$ 得到 $F(w)=\frac{1}{m}||Xw-y||^2$ 均方误差 $F(x)_{min}$ ，
从这个角度来看， $w$ 作为自变量，每一个确定的 $w$ 经过运算都能得到一个 $F (w)$ ,假设 $w$ 是一维数据，固然可以做出一张二维视图< $w$ , $F$ >，类似于下图：

按照线性回归的解题思路是：

对 $F (x)$ 求 $w$ 的偏导，得到 $\bigtriangledown F(w) = \frac{2}{m}X^T(Xw-y)$
令 $\bigtriangledown F(w)=0$ ,（高中知识：求导等于0的点是原方程的极值点）得到唯一解 $w^*=(X^TX)^{-1}X^TY$
求解2.的方程就能得到唯一解 $w^*$ 的值

按照梯度下降的解题思路是：

对 $F (x)$ 求 $w$ 的偏导，得到 $\bigtriangledown F(w) = \frac{2}{m}X^T(Xw-y)$
给定初始 $w$ ，循环次数 $N$ ，学习率 $η$ 。
$w←w-η\bigtriangledown F(w)$ 循环N次，得到的 $w$ 近似的等于 $w^*$

总结梯度下降思路：

梯度下降算法从空间中任一给定初始点开始进行指定轮数的搜索。
在每一轮搜索中都计算目标函数在当前点的梯度，并沿着与梯度相反的方向按照一定步长移动到下一可行点

目标函数要求：

目标函数可微
目标函数必须是凸函数或者强凸函数

脱离线性回归问题，将梯度下降算法步骤抽象出来就是这样：

随机梯度下降

按照梯度下降的解题思路是：

对 $F (x)$ 求 $w$ 的偏导，得到 $\bigtriangledown F(w) = \frac{2}{m}X^T(Xw-y)$
给定初始 $w$ ，循环次数 $N$ ，学习率 $η$ 。
$w←w-η\bigtriangledown F(w)$ 循环N次，得到的 $w$ 近似的等于 $w^*$

特点：

每次 $w←w-η\bigtriangledown F(w)$ 的变化，要计算所有数据（X）上的经验损失的梯度的平均值，求得最后的w值，共耗时m*N。适合数据规模不大，它的稳定性强。

按照随机梯度下降的解题思路是：

对 $F (x)$ 求 $w$ 的偏导，得到 $\bigtriangledown F(w) = \frac{2}{m}X^T(Xw-y)$
给定初始 $w$ ，循环次数 $N$ ，学习率 $η_0,η_1$ 。
$w←w-\frac{η_0}{η_1+t}\bigtriangledown F(w)_{x_{rand(i)}}$ , $w_{sum}←w_{sum}+w$ 循环N次，得到的 $w / N$ 近似的等于 $w^*$

不同之处：

$\bigtriangledown F(w)_{x_{rand(i)}}$ 为任意一个样本 $x_i$ 状态下的 $w_i$ 时刻的梯度，每次循环计算量变为原来梯度的1/m。

脱离线性回归问题，将随机梯度下降算法步骤抽象出来就是这样：

特点：

每次 $w←w-\frac{η_0}{η_1+t}\bigtriangledown F(w)_{x_{rand(i)}}$ 的变化，只需要计算抽样的数据（ $x_i$ ）上的经验损失，求得最后的w值，共耗时N。适合数据规模较大，它的稳定性弱

对于随机梯度和梯度计算的梯度数据量问题：
简单来说是梯度下降每次循环计算的是这个式子的梯度

而随机梯度下降是这个式子的梯度

例子：随机梯度下降和梯度下降的比较

例4.7 ：
用Sklearn工具库中的make_regression函数来随机生成一个线性回归问题。
分别采用梯度下降与随机梯度下降算法求解回归问题。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression


class LinearRegressionSGD:
    def __init__(self):
        self.w = None

    def fit(self, X, y, eta_0=10, eta_1=50, N=1000):
        m, n = X.shape
        w = np.zeros((n, 1))
        self.w = w
        W = np.zeros((N, 2))
        for t in range(N):
            W[t][0] = w[0]
            W[t][1] = w[1]
            i = np.random.randint(m)
            x = X[i].reshape(1, -1)  # 这里使用 (1,-1) 表示将数组重塑为1行，第二维的长度自动计算得出。将结果赋值给变量 x
            e = x.dot(w) - y[i]
            gradient = 2 * e * x.T
            w = w - eta_0 * gradient / (t + eta_1)
            self.w += w
        self.w /= N
        plt.figure(0)
        plt.scatter(W[:, 0], W[:, 1], s=15)
        plt.plot(W[:, 0], W[:, 1])

    def predict(self, X):
        return X.dot(self.w)


class LinearRegression:
    def __init__(self):
        self.w = None

    def fit(self, X, y, eta, N=1000):
        m, n = X.shape
        w = np.zeros((n, 1))
        W = np.zeros((N, 2))
        for t in range(N):
            W[t][0] = w[0]
            W[t][1] = w[1]
            e = X.dot(w) - y
            g = 2 * X.T.dot(e) / m
            w = w - eta * g
        self.w = w
        plt.scatter(W[:, 0], W[:, 1], s=15)
        plt.plot(W[:, 0], W[:, 1])

    def predict(self, X):
        return X.dot(self.w)


X, y = make_regression(n_samples=100, n_features=2, noise=0.1, bias=0, random_state=0)
y = y.reshape(-1, 1)
model = LinearRegression()
model.fit(X, y, eta=0.01, N=1000)
print(model.w)

model = LinearRegressionSGD()
model.fit(X, y, eta_0=10, eta_1=50, N=1000)
print(model.w)

plt.show()

次梯度下降算法

当目标函数不可微的时候，需要将梯度的概念推广到次梯度

次梯度(subgradient)是凸优化中的一个概念。在凸优化中，次梯度是对于非光滑凸函数的梯度的一种泛化。对于一个非光滑且凸的函数 $f (x)$ ，如果 $x$ 是 $f (x)$ 的极小值点，那么就必须满足 $\in \partial f(x)$ 。其中 $\partial f(x)$ 为 $f (x)$ 在点 $x$ 处的次梯度集合，它可以被定义为一个包含所有可能的子梯度的集合。
对于一个可微的函数，其梯度就是唯一的，但是对于一个非光滑的凸函数，其梯度并不唯一，因为它在某些点上可能是不可导的。在这种情况下，次梯度的概念就派上用场了。次梯度可以被看作是梯度的一个推广，它允许我们在非光滑凸函数上进行优化。

次梯度的概念

次梯度定义：
设 $F:R^n→R$ 为一个n元函数。如果 $w,v\in R^n$ 满足如下性质： $F(u)\ge F(w)+<v,u-w>,\forall u\in R^n$

称 $v$ 是F在 $w$ 处的一个次梯度。
称集合 $\partial F(w)=\{v\in R^n,v是F在w处的次梯度\}$ 为F在w处的次梯度集。

定理：
如果 $F:R^n→R$ 是一个凸函数，且在 $w$ 处可微，则 $\partial F(w) =\{\bigtriangledown F(w)\}$ 。

在数学中，符号 $\nabla$ （读作“del”）通常表示梯度（gradient）运算符，用于表示多元函数在某一点处的方向导数最大的方向和大小。 $\nabla$ 通常用于表示可微函数的梯度，它是一个向量，包含了函数在每个自变量方向上的偏导数值。
符号 $\partial$ （读作“partial”）通常表示偏导数（partialderivative），用于表示多元函数在某一点处，对某个自变量的导数。 $\partial$ 通常用于表示不可微函数的导数，它是一个标量，表示函数在某个自变量方向上的变化率。
因此， $\nabla$ 和 $\partial$ 的主要区别在于它们所表示的对象不同： $\nabla$ 表示向量梯度， $\partial$ 表示标量偏导数。同时， $\nabla$ 通常用于表示可微函数的梯度， $\partial$ 则用于表示不可微函数的导数。

举例： Lasso回归优化算法

定义（Lasso回归）： $minF(w)=\frac{1}{m}||Xw-y||^2+\lambda|w|$ 称为Lasso回归，其中， $\lambda(\lambda>0)$ 为正则化系数（L1正则化）
那么，从目标函数可以看出：

次梯度下降算法是适合于求解Lasso回归的优化算法

# Lasso回归优化算法
import numpy as np

 class Lasso:
 	def __init__(self, Lambda=1): #L1正则化系数λ
 		self.Lambda = Lambda

 	def fit(self, X, y, eta=0.1, N=1000):
		m,n = X.shape
 		w = np.zeros((n,1))
 		self.w = w
 		for t in range(N):
			e = X.dot(w) - y
 			v = 2 * X.T.dot(e) / m + self.Lambda * np.sign(w) # λ|w|的次梯度
			w = w - eta * v
			self.w += w
		self.w /= N #w取平均值

	def predict(self, X):
		return X.dot(self.w)

小梯度下降算法

小批量梯度下降（Mini-batch Gradient Descent）是介于批量梯度下降和随机梯度下降之间的一种优化算法。它的思想是将训练数据划分成若干个小的批次，每个批次包含m个样本，然后对每个批次进行梯度下降更新参数。相比于批量梯度下降，小批量梯度下降可以减少计算量，加速收敛，并且相对于随机梯度下降，可以更好地利用GPU的并行计算能力。
因此，小批量梯度下降是两者之间的一种平衡方案，具有较快的收敛速度和更好的收敛性能。

抽象出来，解题过程：

### 示例：线性回归的小批量梯度下降算法

import numpy as np

 class LinearRegression:
 	def fit(self, X, y, eta_0=10, eta_1=50, N=3000, B=10):
 		m, n = X.shape
 		w = np.zeros((n,1))
		self.w = w
 		for t in range(N):
 			batch = np.random.randint(low=0, high=m, size=B)
 			X_batch = X[batch].reshape(B,-1)
 			y_batch = y[batch].reshape(B,-1)
 			e = X_batch.dot(w) - y_batch
 			g = 2 * X_batch.T.dot(e) / B
			w = w - eta_0 * g / (t + eta_1)
 			self.w += w
		self.w /= N

def predict(self, X):
	return X.dot(self.w

坐标下降算法

坐标下降算法优于梯度下降算法的两个场合：

梯度不存在或梯度函数较为复杂难以计算；
需要求解带约束的优化问题

坐标下降算法的搜索过程：

每一步选取一个要调整的坐标分量，且固定参数的其它各分量的值。然着
沿着选取分量的坐标轴方向移动，到达该方向上目标函数值最小的那个点。
如此循环，使用不同的坐标方向，直至沿任何一个坐标移动都无法降低目标函数值为止。

一般情况：

给定 $w\in R,$ 对任意 $1... j ... n$
- $w_{-j}=(w_1,w_2,...,w_{j-1},w_{j+1},...,w_n)$ 为w中除第 j 个分量外其它分量构成的向量。
- 对任意的 $u\in R,(u,w_{-j})=(w_1,w_2,...,w_{j-1},u,w_{j+1},...,w_n)$ 为将w 的第 j 个分量换成 u 构成的向量。