原创不易,转载前请注明博主的链接地址:Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境:
运行平台: Windows
Python版本: Python3.x
IDE: PyCharm

一、Exceptation-Maximization Algorithm理解
文章从最大似然到EM算法浅解中介绍的这个男女生的例子很具有代表性,形象的说明了Exceptation-Maximization Algorithm的背景,首先看一下这个例子:
再回到例子本身,如果没有“男的左边,女的右边,其他的站中间!”这个步骤,或者说我抽到这200个人中,某些男生和某些女生一见钟情,已经好上了,纠缠起来了。咱们也不想那么残忍,硬把他们拉扯开。那现在这200个人已经混到一起了,这时候,你从这200个人(的身高)里面随便给我指一个人(的身高),我都无法确定这个人(的身高)是男生(的身高)还是女生(的身高)。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的,还是女生的那个身高分布抽取的。用数学的语言就是,抽取得到的每个样本都不知道是从哪个分布抽取的。
这个时候,对于每一个样本或者你抽取到的人,就有两个东西需要猜测或者估计的了,一是这个人是男的还是女的?二是男生和女生对应的身高的高斯分布的参数是多少?
实际上,Exceptation-Maximization Algorithm要解决的问题是:具有隐变量的混合模型的参数估计。也就是上文提的那个例子,如果男女分开,可以直接对男女惊喜见面,求出身高的分布即可;但是,如果男女混合,随便抽出来的一个人,并不知道TA是男还是女,并且对TA进行参数估计。这样就是Exceptation-Maximization Algorithm要解决的问题了
既然已经知道,Exceptation-Maximization Algorithm是来干什么的,那Exceptation-Maximization Algorithm的又是怎么解决具有隐变量的混合模型的参数估计问题呢?接下来还是看一下文章从最大似然到EM算法浅解中分苹果的那个例子。
例如,小时候,老妈给一大袋糖果给你,叫你和你姐姐等分,然后你懒得去点糖果的个数,所以你也就不知道每个人到底该分多少个。咱们一般怎么做呢?先把一袋糖果目测的分为两袋,然后把两袋糖果拿在左右手,看哪个重,如果右手重,那很明显右手这代糖果多了,然后你再在右手这袋糖果中抓一把放到左手这袋,然后再感受下哪个重,然后再从重的那袋抓一小把放进轻的那一袋,继续下去,直到你感觉两袋糖果差不多相等了为止。呵呵,然后为了体现公平,你还让你姐姐先选了。
实际上,上面这个例子,可以这么解读:你拿到了待分的苹果,此时不知道改如何分,但是也不能一直僵着呀,于是你打破僵局,将苹果粗略的分到了两个袋子(设置待估计值的初值),然后,为了公平起见(为了达到最优化,也就是待估计值达到最优解(最大值)),你一次次平衡两个袋子中的苹果,这个过程不是一蹴而就的,你这样平衡很多次(迭代很多次),最终达到了,你认为的两个袋子里的苹果一样多的结果(实现的待估计值的最优化问题)。这样,可以总结出Exceptation-Maximization Algorithm的基本过程:设置初值、多次迭代、求得最优(个人总结,欢迎批评指正)
同时,最大期望算法经过两个步骤交替进行计算 :
1)计算期望(E),利用概率模型参数的现有估计值,计算隐藏变量的期望;
2)最大化(M),利用E 步上求得的隐藏变量的期望,对参数模型进行最大似然估计。
3)M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
E步骤:估计未知参数的期望值,给出当前的参数估计。
M步骤:重新估计分布参数,以使得数据的似然性最大,给出未知变量的期望估计。
二、Exceptation-Maximization Algorithm公式推导
实际上,对于解决一般性问题,可以直接用MLE(MaximumLikelihood Estimation)来求得解析解。如下

但是对于含有隐变量的混合模型来讲,求得解析解就比较困难了,而是通过EM来完成,EM的完整表达式如下:
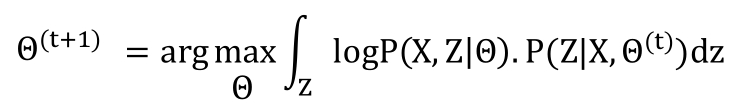
E-STEP:
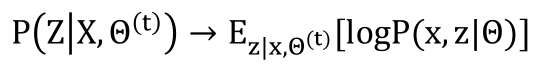
M-STEP:
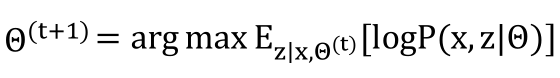
收敛性:
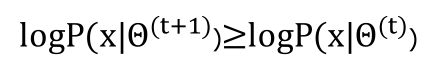
可以看出这是一个迭代算法,其中,
θ是待估计量parameter,
Z是隐变量unobserved data(latent variable),
X是给定数据observed data,
θ(t)是t时刻的参数,他是一个常数(因为在当前时刻,已经得到了t时刻的值了),
(X,Z):complete data
给出EM的完整表达式之后,接下来,了解一些推导过程中用到的内容:

在E-Step中通过上一个θ(t)求得的当前的期望,然后华东M-Step中的θ,使得M-Step中的θ(t+1)达到最大,并不断更新,知道找到最终是θ最大的那个值。
接下来通过利用Jensen Inquality来推导出EM(Exceptation-Maximization Algorithm)表达式:
2.1 Jensen Inquality
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么
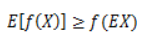
特别地,如果f是严格凸函数,那么上面不等式等号成立是满足:
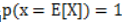
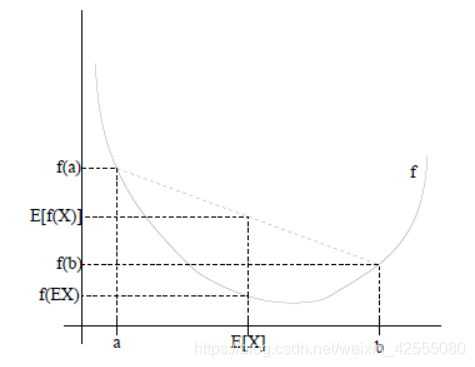
如上图所示:
图中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。(就像掷硬币一样)。X的期望值就是a和b的中值了,图中可以看到:
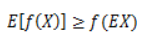
Jensen不等式应用于凹函数时,不等号方向反向,也就是
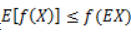
2.2 一种推导

这里直接给出手写版本,如果有不明白的地方欢迎交流讨论。
2.3 另外一种推导

这里依然直接给出手写版本,如果有不明白的地方欢迎交流讨论。
三 实例验证
我们用论文What is the expectation maximization algorithm?
中介绍的抛硬币的例子来深刻认识EM算法。
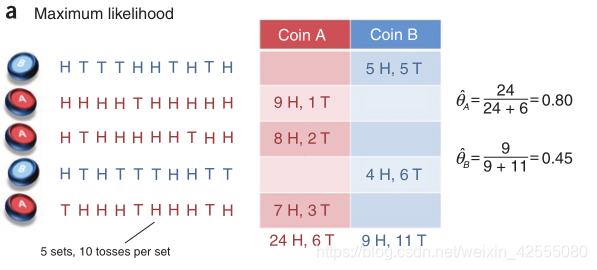
如下图:H表示正面向上,T表示反面向上,参数θ表示正面朝上的概率。硬币有两个,A和B,硬币是有偏的。本次实验总共做了5组,每组随机选一个硬币,连续抛10次。如果知道每次抛的是哪个硬币,那么计算参数θ就非常简单了,如上图所示。
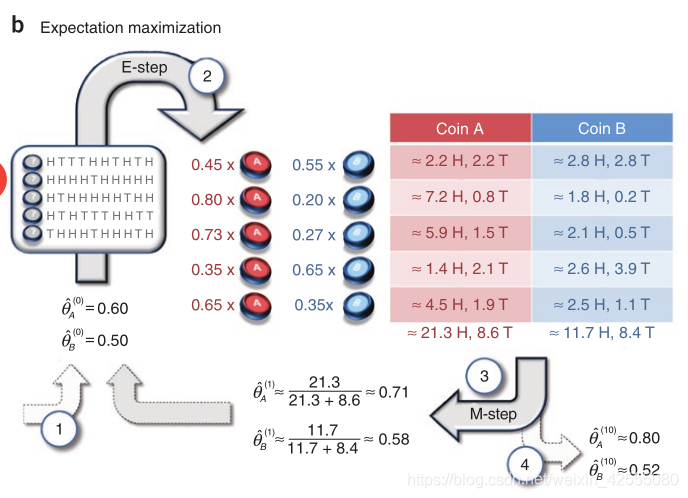
如果不知道每次抛的是哪个硬币呢?那么,我们就需要用EM算法,基本步骤为:1、给θA和θB一个初始值;2、(E-step)估计每组实验是硬币A的概率(本组实验是硬币B的概率=1-本组实验是硬币A的概率)。分别计算每组实验中,选择A硬币且正面朝上次数的期望值,选择B硬币且正面朝上次数的期望值;3、(M-step)利用第三步求得的期望值重新计算θA和θB;4、当迭代到一定次数,或者算法收敛到一定精度,结束算法,否则,回到第2步。
用代码实现如上过程:
首先这里面用到的是scipy库和numpy库
#导入的时候用from scipy import stats #利用这个进行概率的计算
此处注意:不能用 import scipy,因为stats根本不在scipy里边,他是一个单独的stats.py文件,并不是scipy里边的一个子类,所以用import scipy后,scipy.stats就是错误的写法,必须用from import。
from scipy import stats
import numpy as np
构建观测数据集
针对这个问题,首先采集数据,用1表示H(正面),0表示T(反面):
#硬币投掷结果观测序列
observations = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
[1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
[1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
[0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])
第一步:参数的初始化
参数赋初值
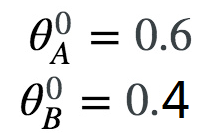
第一个迭代的E步
抛硬币是一个二项分布,可以用scipy中的binom来计算。对于第一行数据,正反面各有5次,所以:
#二项分布求解公式
contribution_A = scipy.stats.binom.pmf(num_heads,len_observation,theta_A)
contribution_B = scipy.stats.binom.pmf(num_heads,len_observation,theta_B)
将两个概率正规化,得到数据来自硬币A,B的概率:
weight_A = contribution_A / (contribution_A + contribution_B)
weight_B = contribution_B / (contribution_A + contribution_B)
这个值类似于三硬币模型中的μ,只不过多了一个下标,代表是第几行数据(数据集由5行构成)。同理,可以算出剩下的4行数据的μ。
有了μ,就可以估计数据中AB分别产生正反面的次数了。μ代表数据来自硬币A的概率的估计,将它乘上正面的总数,得到正面来自硬币A的总数,同理有反面,同理有B的正反面。
#更新在当前参数下A,B硬币产生的正反面次数
counts['A']['H'] += weight_A * num_heads
counts['A']['T'] += weight_A * num_tails
counts['B']['H'] += weight_B * num_heads
counts['B']['T'] += weight_B * num_tails
第一个迭代的M步
当前模型参数下,AB分别产生正反面的次数估计出来了,就可以计算新的模型参数了:
new_theta_A = counts['A']['H']/(counts['A']['H'] + counts['A']['T'])
new_theta_B = counts['B']['H']/(counts['B']['H'] + counts['B']['T'])
### 完整的EM单个迭代
于是就可以整理一下,给出EM算法单个迭代的代码:
```java
def singleCircle_EM(priors, observations):
"""
EM算法单次迭代
:param priors:[theta_A, theta_B]
:param observations:[m X n matrix]
:return:new_priors: [new_theta_A, new_theta_B]
"""
#利用counts变量来记录A硬币正面、背面朝上的次数,B硬币正面、背面朝上的次数
counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
#拿到获取来的初值
theta_A = priors[0]
theta_B = priors[1]
# E step
for observation in observations:
len_observation = len(observation)
#正面朝上的个数
num_heads = observation.sum()
#反面朝上的个数
num_tails = len_observation - num_heads
#二项式分布函数stats.binom.pmf(k,n,p) 表示从n次测量中获得k次的概率,p为随机一次的概率(相当于抽样概率)
#此概率是变化的,所以是可以进行迭代的
contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A)
contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B) # 两个二项分布
#计算权值
weight_A = contribution_A / (contribution_A + contribution_B)
weight_B = contribution_B / (contribution_A + contribution_B)
# 更新在当前参数下A、B硬币产生的正反面次数
counts['A']['H'] += weight_A * num_heads
counts['A']['T'] += weight_A * num_tails
counts['B']['H'] += weight_B * num_heads
counts['B']['T'] += weight_B * num_tails
# M step
#求权值
new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
return [new_theta_A, new_theta_B]
多次迭代,求最优化
def iterationForResult(observations, prior, tol=1e-6, iterations=10000):
"""
EM算法
:param observations: 观测数据
:param prior: 模型初值
:param tol: 迭代结束阈值
:param iterations: 最大迭代次数
:return: 局部最优的模型参数
"""
#给定循环的两个终止条件:模型参数变化小于阈值;循环达到最大次数,就可以写出EM算法的主循环了
iteration = 0
while iteration < iterations:
new_prior = singleCircle_EM(prior, observations)
print(new_prior[0])
#判断初值的theta_A与当前的theta_A两个值的变化(绝对值)是否超过阈值
delta_change = np.abs(prior[0] - new_prior[0])
if delta_change < tol:
break
else:
prior = new_prior
iteration += 1
return [new_prior, iteration]
通过函数调用求解
result = iterationForResult(observations, [0.6, 0.4])
print(result)
结果
可以看到共有13次迭代就已经达到约束条件下的最优解,前十三次迭代第一个变量的值,如下。13次迭代的最终结果展示如下最后一列。
0.7261346175962778
0.7679650080356558
0.7851830994553255
0.7922578783453181
0.7950515886589887
0.79612806787534
0.7965383712512938
0.7966940909872233
0.7967530973878143
0.7967754449561374
0.7967839077490712
0.7967871126803284
0.7967883265564044
0.7967887863838075
[[0.7967887863838075, 0.51958314107701], 13]
四 总结
算法里已知的是观察数据,未知的是隐含数据和模型参数,在E步,所做的事情是固定模型参数的值,优化隐含数据的分布,而在M步,我们所做的事情是固定隐含数据分布,优化模型参数的值。 EM算法有很多的应用,最广泛的就是GMM混合高斯模型、聚类、HMM等等。
这篇文章就到这里了,欢迎大佬们多批评指正,也欢迎大家积极评论多多交流。

参考文章
1 从最大似然到EM算法浅解
2 (EM算法)The EM Algorithm
3 【机器学习算法系列之一】EM算法实例分析
4 EM算法整理及其python实现
5 EM算法详解和numpy代码实现
6 EM算法–应用到三个模型: 高斯混合模型 ,混合朴素贝叶斯模型,因子分析模型
7 EM算法**********
8 EM算法整理及其python实现
9 EM算法的python实现
附完整代码
from scipy import stats
import numpy as np
# 硬币投掷结果观测序列
observations = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
[1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
[1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
[0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])
def singleCircle_EM(priors, observations):
"""
EM算法单次迭代
:param priors:[theta_A, theta_B]
:param observations:[m X n matrix]
:return:new_priors: [new_theta_A, new_theta_B]
"""
#利用counts变量来记录A硬币正面、背面朝上的次数,B硬币正面、背面朝上的次数
counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
#拿到获取来的初值
theta_A = priors[0]
theta_B = priors[1]
# E step
for observation in observations:
len_observation = len(observation)
#正面朝上的个数
num_heads = observation.sum()
#反面朝上的个数
num_tails = len_observation - num_heads
#二项式分布函数stats.binom.pmf(k,n,p) 表示从n次测量中获得k次的概率,p为随机一次的概率(相当于抽样概率)
#此概率是变化的,所以是可以进行迭代的
contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A)
contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B) # 两个二项分布
#计算权值
weight_A = contribution_A / (contribution_A + contribution_B)
weight_B = contribution_B / (contribution_A + contribution_B)
# 更新在当前参数下A、B硬币产生的正反面次数
counts['A']['H'] += weight_A * num_heads
counts['A']['T'] += weight_A * num_tails
counts['B']['H'] += weight_B * num_heads
counts['B']['T'] += weight_B * num_tails
# M step
#求权值
new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
return [new_theta_A, new_theta_B]
def iterationForResult(observations, prior, tol=1e-6, iterations=10000):
"""
EM算法
:param observations: 观测数据
:param prior: 模型初值
:param tol: 迭代结束阈值
:param iterations: 最大迭代次数
:return: 局部最优的模型参数
"""
#给定循环的两个终止条件:模型参数变化小于阈值;循环达到最大次数,就可以写出EM算法的主循环了
iteration = 0
while iteration < iterations:
new_prior = singleCircle_EM(prior, observations)
print(new_prior[0])
#判断初值的theta_A与当前的theta_A两个值的变化(绝对值)是否超过阈值
delta_change = np.abs(prior[0] - new_prior[0])
if delta_change < tol:
break
else:
prior = new_prior
iteration += 1
return [new_prior, iteration]
if __name__ == "__main__":
result = iterationForResult(observations, [0.6, 0.4])
print(result)