学习完机器学习实战的支持向量机，简单的做个笔记。文中部分描述属于个人消化后的理解，仅供参考。

本篇综合了先前的文章，如有不理解，可参考：

吴恩达机器学习（十）支持向量机

所有代码和数据可以访问我的 github

如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~

0. 前言

支持向量机（Support Vector Machine）是一类监督学习的二分类算法。

通过构建超平面，将数据分割开来，超平面一边的数据属于同一类别。

支持向量是指距离分割超平面最近的那些点，支持向量机目的是使得支持向量到超平面的间隔最大。

优点：泛化错误率低，结果易于解释
对参数调节和核函数的选择敏感
适用数据类型：数值型和标称型数据

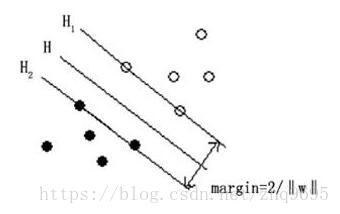
如下图所示（图源：百度百科）：

$H$ 为分割超平面，在超平面上下方各建立一个界面 $H_1$ 和 $H_2$ ，在 $H_1$ 之上的为一类，在 $H_2$ 之下的为一类。

SVM的目的是为了最大化间隔，即 $H_1$ 到 $H_2$ 的距离。

1. 寻找最大间隔

在SVM中，定义正类 $y=1$ ，定义反类 $y=-1$ ，这是为了方便后面计算。

通过 $w^Tx+b=0$ 拟合数据的分界线，即超平面，则可定义上界面为 $w^Tx+b=1$ ，下界面为 $w^Tx+b=-1$ 。因可以通过改变系数的倍数表示距离，所以可粗略定义为 $1$ 。

上界面以上的点表示为 $w^Tx+b\geqslant 1,\ y=1$ ，下界面以下的点表示为 $w^Tx+b\leqslant -1,\ y=-1$ ，所以综合可得 $y(w^Tx+b)\geqslant 1$ 。

需最大化上界面到下界面的距离：

$d=\frac{\left|c_2-c_1\right|}{\sqrt{w_1^2+...+w_n^2}}=\frac{2}{\left\|w\right\|}$

$\max\ d\Rightarrow \min\ \frac{\left\|w\right\|}{2}\Rightarrow \min\ \frac{\left\|w\right\|^2}{2}\Rightarrow \min\ \frac{1}{2}w^Tw$

所以，可得目标函数和约束条件：

$\left\{\begin{align*} &\min\ \frac{1}{2}w^Tw\\ &s.t.\ y^{(i)}(w^Tx^{(i)}+b)\geqslant 1 \end{align*}\right.$

2. 拉格朗日乘子法和KKT条件

拉格朗日乘子法：求在约束条件下，函数的极值问题
KKT条件：若约束条件为不等式，则需满足一定条件

在拉格朗日乘子法中，引入了其他的参数，并将原问题转换为对偶问题（求最小值转换为求最大值）。

首先修改目标函数和约束条件为：

$\left\{\begin{align*} &\min\ \frac{1}{2}w^Tw\\ &s.t.\ y^{(i)}(w^Tx^{(i)}+b)\geqslant 1 \end{align*}\right. \Rightarrow \left\{\begin{align*} &\min\ \frac{1}{2}w^Tw\\ &s.t.\ 1-y^{(i)}(w^Tx^{(i)}+b)\leqslant 0\end{align*}\right.$

应用拉格朗日乘子法：

$\begin{align*} L(w,b,\alpha) &= \frac{1}{2}w^Tw+\alpha_1g_1(x)+...+\alpha_ng_n(x) \\ &= \frac{1}{2}w^Tw -\alpha_1(y^{(1)}(w^Tx^{(1)}+b)-1)-...-\alpha_n(y^{(n)}(w^Tx^{(n)}+b)-1) \\ &= \frac{1}{2}w^Tw -\sum_{i=1}^{m}\alpha_iy^{(i)}(w^Tx^{(i)}+b)+\sum_{i=1}^{m}\alpha_i \end{align*}$

应满足的KKT条件为：

$\begin{align*} &\frac{\partial L}{\partial w} = w-\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)}=0 \Rightarrow w=\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)} \\ &\frac{\partial L}{\partial b} = -\sum_{i=1}^{m}\alpha_iy^{(i)}=0 \Rightarrow \sum_{i=1}^{m}\alpha_iy^{(i)}=0 \\ &\alpha \geqslant 0 \end{align*}$

将KKT条件代回拉格朗日乘子法：

$\begin{align*} L(w,b,\alpha) &= \frac{1}{2}(\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)})^T(\sum_{j=1}^{m}\alpha_jy^{(j)}x^{(j)}) -\sum_{i=1}^{m}\alpha_iy^{(i)}((\sum_{j=1}^{m}\alpha_jy^{(j)}x^{(j)})^Tx^{(i)}+b)+\sum_{i=1}^{m}\alpha_i \\ &= -\frac{1}{2}\sum_{i,j=1}^{m}\alpha_iy^{(i)}\alpha_jy^{(j)}(x^{(i)})^Tx^{(j)}+b\sum_{i=1}^{m}\alpha_iy^{(i)}+\sum_{i=1}^{m}\alpha_i \\ &= \sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{m}\alpha_iy^{(i)}\alpha_jy^{(j)}(x^{(i)})^Tx^{(j)} \end{align*}$

因转换为对偶问题，所以此时目标函数和约束条件：

$\left\{\begin{align*} &\max\ w(\alpha)=L(w,b,\alpha)\\ &s.t.\ \alpha \geqslant 0 \\ &s.t.\ \sum_{i=1}^{m}a_iy^{(i)}=0 \end{align*}\right.$

3. 松弛变量

有时，数据并非 $100\%$ 线性可分，有一部分数据会在上下界面之间，或者处于错误的类别。

此时可增加一个松弛变量 $\epsilon _i\ (\epsilon _i \geqslant 0)$ ，允许有数据点位于错误的一侧。

定义上界面以上为 $w^Tx+b\geqslant 1-\epsilon _i,\ y=1$ ，下界面以下为 $w^Tx+b\leqslant -1+\epsilon _i,\ y=-1$ ，可综合为 $y(w^Tx+b)\geqslant 1-\epsilon _i$

所以，可得目标函数和约束条件，其中 $C$ 是控制权重：

$\left\{\begin{align*} &\min\ \frac{1}{2}w^Tw+C\sum_{i=1}^{m}\epsilon_i\\ &s.t.\ y^{(i)}(w^Tx^{(i)}+b)\geqslant 1-\epsilon _i \end{align*}\right.$

4. 带松弛变量的拉格朗日乘子法和KKT条件

同理，根据拉格朗日乘子法和KKT条件，可得：

$L(w,b,\alpha) = \sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i,j=1}^{m}\alpha_iy^{(i)}\alpha_jy^{(j)}(x^{(i)})^Tx^{(j)}$

所以，目标函数和约束条件为：

$\left\{\begin{align*} &\max\ w(\alpha)=L(w,b,\alpha)\\ &s.t.\ C\geqslant \alpha \geqslant 0 \\ &s.t.\ \sum_{i=1}^{m}a_iy^{(i)}=0 \end{align*}\right.$

5. 序列最小优化SMO（Sequential Minimal Optimization）

SMO算法的目标是求出一系列的 $\alpha$ 和 $b$ ，然后通过一开始的KKT条件，得出权重 $w$ ：

$w=\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)}$

SMO算法的工作原理是，每次循环都选择两个 $\alpha$ ，同时对两个 $\alpha$ 进行优化。

因需满足 $\sum_{i=1}^{m}a_iy^{(i)}=0$ ，所以增大其中一个 $\alpha$ 的同时，减小另一个 $\alpha$ 。

6. 高斯核函数（Gaussian Kernel）

若数据是非线性可分，就无法使用线性的SVM进行解决。

可通过核函数，将低维空间中的数据映射到高维空间中，可将一个在低维空间中的非线性问题转换为高维空间下的线性问题求解。

高斯核函数的定义如下，其中 $\sigma$ 表示到达率（函数值跌落到 $0$ 的速度参数）， $\sigma$ 越小，支持向量越多：

$k(x,l)=\exp(-\frac{\left\|x-l\right\|^2}{2\sigma^2})$

其中， $\large l$ 称为标记点， $\large l^{(1)},l^{(2)},...,l^{(m)}$ ，每一个标记点与每一个样本数据在空间中位于相同位置。所以有：

如果 $x$ 与 $l$ 相近 $\Rightarrow f\approx exp(0)\approx1$
如果 $x$ 与 $l$ 相隔远 $\Rightarrow f=exp(-\infty )\approx0$

超平面的定义如下：

$\begin{align*} w^Tx+b &= (\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)})^Tx+b \\ &= \sum_{i=1}^{m}\alpha_iy^{(i)}(x^{(i)})^Tx+b \end{align*}$

可使用核函数，替换向量的内积：

$\begin{align*} w^Tx+b &= (\sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)})^Tx+b \\ &= \sum_{i=1}^{m}\alpha_iy^{(i)}(x^{(i)})^Tx+b \\ &= \sum_{i=1}^{m}\alpha_iy^{(i)}k(x,x^{(i)})+b \end{align*}$

高斯核函数的SVM流程可表示为：

给定数据集 $(x^{(1)},y^{(1)}),...,(x^{(m)},y^{(m)})$
SMO算法计算 $\alpha$ 和 $b$
高斯核函数计算 $k(x,x^{(1)}),...,k(x,x^{(m)})$
代入 $w^Tx+b$ ，判断大于 $0$ 则属于正类，小于 $0$ 则属于反类

7. 实战案例

以下将展示书中案例的代码段，所有代码和数据可以在github中下载：

7.1. 简化版SMO算法案例

# coding:utf-8
from numpy import *

"""
简化版SMO算法案例
"""


# 加载数据集
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


# 根据第i个alpha，从m中选择另一个不同的alpha
def selectJrand(i, m):
    j = i
    while (j == i):
        j = int(random.uniform(0, m))
    return j


# 设定alpha的上界和下界
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


# 简化版本SMO算法，并没有确定优化的最佳alpha对，而是随机选择
# dataMatIn 数据集
# classLabels 类别标签
# C 常数C
# toler 容错率
# maxIter 最大迭代次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    b = 0
    m, n = shape(dataMatrix)
    # alphas的维度为m*1，m为数据集大小
    alphas = mat(zeros((m, 1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            # 预测第i个向量属于的类别
            fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
            # 判断这个预测的误差
            Ei = fXi - float(labelMat[i])
            # 满足KKT条件
            if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
                # 选择另一个向量j
                j = selectJrand(i, m)
                # 预测第j个向量属于的类别
                fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
                # 判断这个预测的误差
                Ej = fXj - float(labelMat[j])
                # 创建alpha i 和alpha j的副本
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()
                # 判断两个类别标签是否相等
                # 设定最大值为0，最小值为C
                if labelMat[i] != labelMat[j]:
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print("L==H")
                    continue
                # 计算最优修改量
                eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - \
                      dataMatrix[i, :] * dataMatrix[i, :].T - \
                      dataMatrix[j, :] * dataMatrix[j, :].T
                if eta >= 0:
                    print("eta>=0")
                    continue
                # 对alpha j作调整
                alphas[j] -= labelMat[j] * (Ei - Ej) / eta
                alphas[j] = clipAlpha(alphas[j], H, L)
                # 如果alpha j只是轻微的调整
                if abs(alphas[j] - alphaJold) < 0.00001:
                    print("j not moving enough")
                    continue
                # alpha a改变大小与alpha j一样，但是方向相反
                alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j])
                # 调整常数项b
                b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T \
                     - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
                b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T \
                     - labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
                if (0 < alphas[i]) and (C > alphas[i]):
                    b = b1
                elif (0 < alphas[j]) and (C > alphas[j]):
                    b = b2
                else:
                    b = (b1 + b2) / 2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
        # 如果没有对任何向量进行修改，则迭代次数+1，否则迭代次数清零
        # 只有在所有迭代中，都没有对alpha进行修改，才能说明所有alpha已经最优
        if alphaPairsChanged == 0:
            iter += 1
        else:
            iter = 0
        print("iteration number: %d" % iter)
    return b, alphas


if __name__ == '__main__':
    dataArr, labelArr = loadDataSet('testSet.txt')
    b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
    print(b)
    print(alphas)

7.2. 完整版SMO算法案例

# coding:utf-8
from numpy import *

"""
完整版SMO算法案例
"""


# 加载数据集
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


# 建立存储各参数的类
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m, 1)))
        self.b = 0
        self.eCache = mat(zeros((self.m, 2)))


# 根据第i个alpha，从m中选择另一个不同的alpha
def selectJrand(i, m):
    j = i
    while (j == i):
        j = int(random.uniform(0, m))
    return j


# 设定alpha的上界和下界
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


# 计算预测误差函数
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * (oS.X * oS.X[k, :].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek


# 内循环寻找第二个alpha
# 启发式方法，最大化步长寻找第二个alpha
def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    # 误差全局缓存赋值
    # 第0个元素表示是否赋值过
    # 第1个元素表示对应误差
    oS.eCache[i] = [1, Ei]
    # 获取所有赋值过的误差全局缓存
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    # 因不能选择当前i,所以需判断数量是否大于1
    # 若是则最大化步长, 若否则随机选择alpha j
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            # 选择最大步长的
            if (deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej


# 更新误差全局缓存
def updateEk(oS, k):
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]


# 完整版SMO，内循环优化
def innerL(i, oS):
    # alpha_i的误差
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) \
            or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 选择alpha_j
        j, Ej = selectJ(i, oS, Ei)
        # 记录原始的alpha
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if oS.labelMat[i] != oS.labelMat[j]:
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print("L==H")
            return 0
        # 计算最优修改量
        eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - \
              oS.X[j, :] * oS.X[j, :].T
        if eta >= 0:
            print("eta>=0")
            return 0
        # 更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        # 更新全局缓存
        updateEk(oS, j)
        if abs(oS.alphas[j] - alphaJold) < 0.00001:
            print("j not moving enough")
            return 0
        # 更新alpha_i
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        # 更新全局缓存
        updateEk(oS, i)
        # 更新常数b
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0


# 完整版SMO，外循环
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        # 完整遍历
        if entireSet:
            for i in range(oS.m):
                alphaPairsChanged += innerL(i, oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 非边界值遍历
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 切换遍历的地方
        if entireSet:
            entireSet = False
        elif alphaPairsChanged == 0:
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b, oS.alphas


# 根据alpha计算权重系数w
def calcWs(alphas, dataArr, classLabels):
    X = mat(dataArr)
    labelMat = mat(classLabels).transpose()
    m, n = shape(X)
    w = zeros((n, 1))
    for i in range(m):
        w += multiply(alphas[i] * labelMat[i], X[i, :].T)
    return w


if __name__ == '__main__':
    dataArr, labelArr = loadDataSet('testSet.txt')
    b, alphas = smoP(dataArr, labelArr, 0.6, 0.001, 40)
    w = calcWs(alphas, dataArr, labelArr)
    print(w)

7.3. 高斯核函数案例

# coding:utf-8
from numpy import *

"""
高斯核函数案例
"""


# 加载数据集
def loadDataSet(fileName):
    dataMat = []
    labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat


# 核函数转换
def kernelTrans(X, A, kTup):
    m, n = shape(X)
    K = mat(zeros((m, 1)))
    # 线性内核
    if kTup[0] == 'lin':
        K = X * A.T
    # 高斯内核
    elif kTup[0] == 'rbf':
        for j in range(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T
        K = exp(K / (-1 * kTup[1] ** 2))
    else:
        raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
    return K


# 存储参数数据结构
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m, 1)))
        self.b = 0
        self.eCache = mat(zeros((self.m, 2)))
        self.K = mat(zeros((self.m, self.m)))
        for i in range(self.m):
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)


# 计算预测的误差
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek


# 根据第i个alpha，从m中选择另一个不同的alpha
def selectJrand(i, m):
    j = i
    while (j == i):
        j = int(random.uniform(0, m))
    return j


# 设定alpha的上界和下界
def clipAlpha(aj, H, L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj


# 内循环寻找第二个alpha
# 启发式方法，最大化步长寻找第二个alpha
def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    # 误差全局缓存赋值
    # 第0个元素表示是否赋值过
    # 第1个元素表示对应误差
    oS.eCache[i] = [1, Ei]
    # 获取所有赋值过的误差全局缓存
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    # 因不能选择当前i,所以需判断数量是否大于1
    # 若是则最大化步长, 若否则随机选择alpha j
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            # 选择最大步长的
            if (deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej


# 更新误差全局缓存
def updateEk(oS, k):
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]


# 完整版SMO，内循环优化
def innerL(i, oS):
    # alpha_i的误差
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) \
            or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 选择alpha_j
        j, Ej = selectJ(i, oS, Ei)
        # 记录原始的alpha
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy();
        if oS.labelMat[i] != oS.labelMat[j]:
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print("L==H")
            return 0
        # 计算最优修改量
        eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]
        if eta >= 0:
            print("eta>=0")
            return 0
        # 更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        # 更新全局缓存
        updateEk(oS, j)
        if abs(oS.alphas[j] - alphaJold) < 0.00001:
            print("j not moving enough")
            return 0
        # 更新alpha_i
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        # 更新全局缓存
        updateEk(oS, i)
        # 更新常数b
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.K[i, j]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.K[j, j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0


# 完整版SMO，外循环
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        # 完整遍历
        if entireSet:
            for i in range(oS.m):
                alphaPairsChanged += innerL(i, oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 非边界值遍历
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 切换遍历的地方
        if entireSet:
            entireSet = False
        elif alphaPairsChanged == 0:
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b, oS.alphas


# 文本转换为向量
def img2vector(filename):
    returnVect = zeros((1, 1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0, 32 * i + j] = int(lineStr[j])
    return returnVect


# 加载数据
def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)
    m = len(trainingFileList)
    trainingMat = zeros((m, 1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9:
            hwLabels.append(-1)
        else:
            hwLabels.append(1)
        trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels


# 测试函数
def testDigits(kTup=('rbf', 10)):
    dataArr, labelArr = loadImages('trainingDigits')
    b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    # 获取所有支持向量
    svInd = nonzero(alphas.A > 0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd]
    print("there are %d Support Vectors" % shape(sVs)[0])
    m, n = shape(datMat)
    errorCount = 0
    for i in range(m):
        # 构建核函数
        kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
        # 利用核函数进行预测
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount) / m))
    dataArr, labelArr = loadImages('testDigits')
    errorCount = 0
    datMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    m, n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]): errorCount += 1
    print("the test error rate is: %f" % (float(errorCount) / m))


if __name__ == '__main__':
    testDigits()

如果这篇文章对你有一点小小的帮助，请给个关注喔~我会非常开心的~

机器学习实战（五）支持向量机SVM（Support Vector Machine）

目录