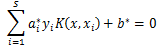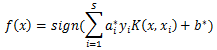求解线性分类问题,线性SVM是一种非常有效的方法,但是有时分类问题是非线性的,这时可以使用非线性SVM。非线性问题往往不好求解,希望能用解线性分类问题的方法解决这个问题,可以采用非线性变换,将非线性问题变换为线性问题,通过解决变换后的线性问题的方法求解原来的非线性问题。
在线性回归中,可以将多项式回归转化为线性回归。比如一个只有两个特征的p次多项式回归模型:
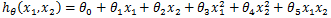 令
令
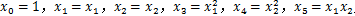 ,得到:
,得到:
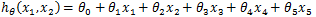 这是一个五元线性回归,可以用线性回归的方法来解决。对于每一个二元样本特征
这是一个五元线性回归,可以用线性回归的方法来解决。对于每一个二元样本特征
 ,得到一个五元样本特征
,得到一个五元样本特征
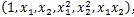 ,通过这个改进的五元样本特征,把不是线性回归的函数变成线性回归。也就是说,对于二维的不是线性的数据,将其映射到五维后就变成了线性数据。这给了我们启发,对于在低维线性不可分的数据,映射到高维后就变成线性可分的了。这个思想同样可以运用到SVM线性不可分数据上。
,通过这个改进的五元样本特征,把不是线性回归的函数变成线性回归。也就是说,对于二维的不是线性的数据,将其映射到五维后就变成了线性数据。这给了我们启发,对于在低维线性不可分的数据,映射到高维后就变成线性可分的了。这个思想同样可以运用到SVM线性不可分数据上。
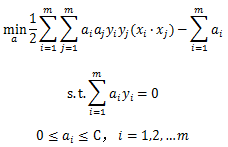 注意到上式低维特征仅以内积
注意到上式低维特征仅以内积
 的形式出现,如果定义一个低维特征空间到高维特征空间的映射,将所有特征映射到一个更高的维度,使数据线性可分,就可以按之前的方法来优化目标函数,求出分离超平面和分类决策函数。现在SVM的优化目标函数变成:
的形式出现,如果定义一个低维特征空间到高维特征空间的映射,将所有特征映射到一个更高的维度,使数据线性可分,就可以按之前的方法来优化目标函数,求出分离超平面和分类决策函数。现在SVM的优化目标函数变成:
 可以看到,和线性SVM的优化目标函数的区别仅仅是将内积
可以看到,和线性SVM的优化目标函数的区别仅仅是将内积
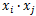 替换为
替换为
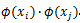 。核函数定义如下:
。核函数定义如下:
假设ϕ是一个从低维的输入空间χ(欧氏空间的子集或离散集合)到高维的希尔伯特空间H的映射,存在函数K(x,z),对于任意x,z∈χ,都有:
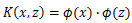 称K(x,z)为核函数。
称K(x,z)为核函数。
K(x,z)的计算是在低维特征空间来计算的,避免了在高维空间计算内积的巨大计算量。核函数的好处在于它在低维上进行计算,而将实质上的分类效果(利用内积)表现在了高维上,避免了直接在高维空间中的复杂计算。对于给定的核函数,特征空间和映射函数的取法并不唯一,可以取不同的特征空间,即便是在同一特征空间里也可以取不同的映射。
正定核函数的充要条件是对任意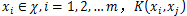 对应的Gram矩阵
对应的Gram矩阵
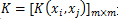 是半正定矩阵。
是半正定矩阵。
这一定义在构造核函数时很有用,但对于一个具体函数来说,检验它是否是正定核函数并不容易,在实际问题中往往应用已有的核函数。
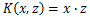 也就是说,线性SVM可以和非线性SVM归为一类,区别仅仅在于线性SVM用的是线性核函数。
也就是说,线性SVM可以和非线性SVM归为一类,区别仅仅在于线性SVM用的是线性核函数。
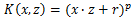 其中r和p都需要自己调参定义。分类决策函数是:
其中r和p都需要自己调参定义。分类决策函数是:
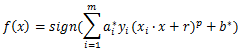
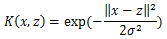 分类决策函数是:
分类决策函数是:
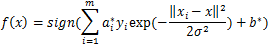
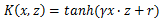
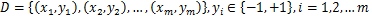
输出:分离超平面参数w*和b*,分类决策函数。
算法:
(1) 选择适当的核函数K(x,z)和惩罚参数C>0,构造并求解约束最优化问题
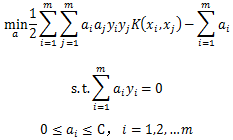 (2) 用SMO算法求出上式最小时对应的a*
(2) 用SMO算法求出上式最小时对应的a*
(3) 计算
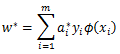 此处可以不直接显式的计算w^*。
此处可以不直接显式的计算w^*。
(4) 找出所有S个支持向量,即满足 对应的样本
对应的样本
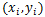 ,通过
,通过
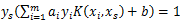 ,计算出每个支持向量对应的
,计算出每个支持向量对应的
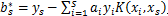 ,
,
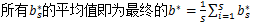
(5) 分离超平面
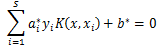 分类决策函数
分类决策函数
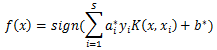
在线性回归中,可以将多项式回归转化为线性回归。比如一个只有两个特征的p次多项式回归模型:
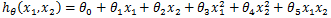
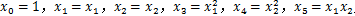 ,得到:
,得到:
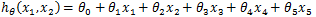
 ,得到一个五元样本特征
,得到一个五元样本特征
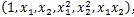 ,通过这个改进的五元样本特征,把不是线性回归的函数变成线性回归。也就是说,对于二维的不是线性的数据,将其映射到五维后就变成了线性数据。这给了我们启发,对于在低维线性不可分的数据,映射到高维后就变成线性可分的了。这个思想同样可以运用到SVM线性不可分数据上。
,通过这个改进的五元样本特征,把不是线性回归的函数变成线性回归。也就是说,对于二维的不是线性的数据,将其映射到五维后就变成了线性数据。这给了我们启发,对于在低维线性不可分的数据,映射到高维后就变成线性可分的了。这个思想同样可以运用到SVM线性不可分数据上。
一、核函数
回顾线性SVM的优化目标函数: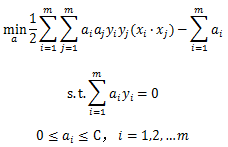
 的形式出现,如果定义一个低维特征空间到高维特征空间的映射,将所有特征映射到一个更高的维度,使数据线性可分,就可以按之前的方法来优化目标函数,求出分离超平面和分类决策函数。现在SVM的优化目标函数变成:
的形式出现,如果定义一个低维特征空间到高维特征空间的映射,将所有特征映射到一个更高的维度,使数据线性可分,就可以按之前的方法来优化目标函数,求出分离超平面和分类决策函数。现在SVM的优化目标函数变成:

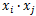 替换为
替换为
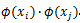 。核函数定义如下:
。核函数定义如下:
假设ϕ是一个从低维的输入空间χ(欧氏空间的子集或离散集合)到高维的希尔伯特空间H的映射,存在函数K(x,z),对于任意x,z∈χ,都有:
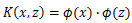
K(x,z)的计算是在低维特征空间来计算的,避免了在高维空间计算内积的巨大计算量。核函数的好处在于它在低维上进行计算,而将实质上的分类效果(利用内积)表现在了高维上,避免了直接在高维空间中的复杂计算。对于给定的核函数,特征空间和映射函数的取法并不唯一,可以取不同的特征空间,即便是在同一特征空间里也可以取不同的映射。
二、正定核函数
已知映射函数ϕ,可以通过ϕ(x)和ϕ(z)的内积求得核函数,不用构造映射能否直接判断一个给定的函数是不是核函数?或者说什么样的函数才能成为核函数?通常所说的核函数都是正定核函数,这里讨论正定核函数的充分必要条件。正定核函数的充要条件是对任意
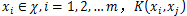 对应的Gram矩阵
对应的Gram矩阵
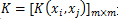 是半正定矩阵。
是半正定矩阵。
这一定义在构造核函数时很有用,但对于一个具体函数来说,检验它是否是正定核函数并不容易,在实际问题中往往应用已有的核函数。
三、常用核函数
3.1 线性核函数
线性核函数(Linear Kernel)其实就是线性SVM,表达式为: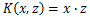
3.2 多项式核函数
多项式核函数(Polynomial Kernel)是非线性SVM常用的核函数之一,表达式为: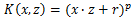
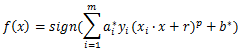
3.3 高斯核函数
高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function, RBF),它是非线性SVM最主流的核函数。libsvm默认的核函数就是它。表达式为: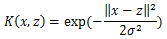
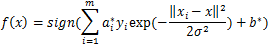
3.4 Sigmoid核函数
Sigmoid核函数(Sigmoid Kernel)也是非线性SVM常用的核函数之一,表达式为: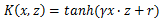
四、非线性SVM算法
输入:样本集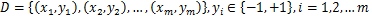
输出:分离超平面参数w*和b*,分类决策函数。
算法:
(1) 选择适当的核函数K(x,z)和惩罚参数C>0,构造并求解约束最优化问题
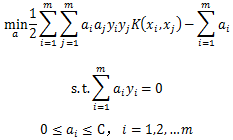
(3) 计算
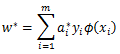
(4) 找出所有S个支持向量,即满足
 对应的样本
对应的样本
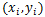 ,通过
,通过
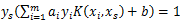 ,计算出每个支持向量对应的
,计算出每个支持向量对应的
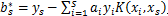 ,
,
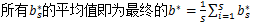
(5) 分离超平面