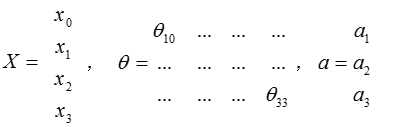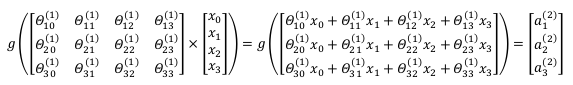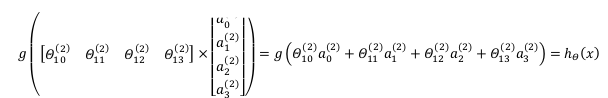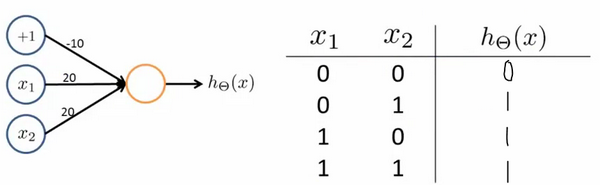机器学习-神经网络(一)

为什么要使用神经网络

当特征太多时，计算的负荷会特别大，而普通的线性回归/逻辑回归都无法有效地处理这么多的特征，这个时候我们需要神经网络。

神经网络的模型表示

首先，我们为神经网络里的每一层都增加了一个偏差单元，即每一层的0号下标的单元，它的值永远为1，而偏差单元我们只在当作输入时使用。

这时，我们把输入的样本特征 $x_0x_1x_2x_3$ 看作第一层输入， $a_1a_2a_3$ 看作第一层的输出，把 $a_0a_1a_2a_3$ 看作第二层的输入， $h_\theta(x)$ 看作第二层的输出。

PS：输出的意思就是经过一个激励函数 $g(z)$ 的运算得出的，这里：
$g(z)=\frac{1}{1+e^{-z}}$
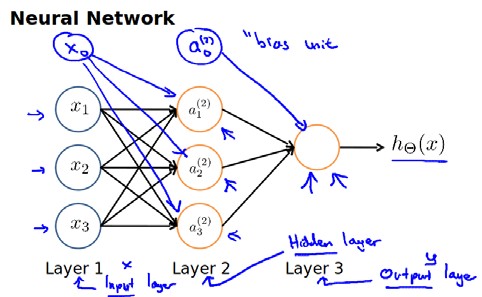
在这里插入图片描述

输出怎么得到

从线性回归中我们能够知道： $h_\theta(x) = \theta_0x_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 = y$

如果我们想要使用相同的输入 $x_0x_1x_2x_3$ 得出一个不一样的 $y_1$ ，我们必须要改变 $\theta$ 的值使得与第一次运算的 $\theta$ 不一样。

同理，当我们把输入的样本特征 $x_0x_1x_2x_3$ 看作第一层输入时，我们就需要三组不同的 $\theta$ 值，使得经过激励函数后得到三个不同的值 $a_1a_2a_3$ 。因此，我们就有了关于第一层输入的 $\theta$ 矩阵 $\Theta^{(1)}$ ，它的尺寸为 3*4。那么第二层输入的 $\theta$ 矩阵 $\theta^{(2)}$ 的尺寸则为 1*4。当然我们也可能会有许多次输入输出，如果我们进行多次的输入输出， $a_{i}^{\left( j \right)}$ 则代表第 $j$ 层的第 $i$ 个激活单元(输入)。 ${\theta }^{\left( j \right)}$ 代表从第 $j$ 层映射到第$ j+1$ 层时的权重的矩阵，例如 ${\theta }^{\left( 1 \right)}$ 代表从第一层映射(输出)到第二层的权重的矩阵。其尺寸为：以第 $j+1$ 层的激活单元数量为行数，以第 $j$ 层的激活单元数加一为列数的矩阵。

输入-输出的过程

因为 $a_1a_2a_3$ 是样本特征 $x_0x_1x_2x_3$ 与 $\Theta^{(1)}$ 经过激励函数后得到的值，因此此过程可写为：

$a_{1}^{2}=g(\Theta_{10}^{1}x_{0}+\Theta_{11}^{1}x_{1}+\Theta_{12}^{1}x_{2}+\Theta_{13}^{1}x_{3})$

$a_{2}^{2}=g(\Theta_{20}^{1}x_{0}+\Theta_{21}^{1}x_{1}+\Theta_{22}^{1}x_{2}+\Theta_{23}^{1}x_{3})$

$a_{3}^{2}=g(\Theta_{30}^{1}x_{0}+\Theta_{31}^{1}x_{1}+\Theta_{32}^{1}x_{2}+\Theta_{33}^{1}x_{3})$

$h_\Theta(x)=g(\Theta_{10}^{2}a_{0}^{2}+\Theta_{11}^{2}a_{1}^{2}+\Theta_{12}^{2}a_{2}^{2}+\Theta_{13}^{2}a_{3}^{2})$

上面进行的讨论中只是将特征矩阵中的一行（一个训练实例）喂给了神经网络，我们需要将整个训练集都喂给我们的神经网络算法来学习模型。

我们可以知道：每一个 $a$ 都是由上一层所有的 $x$ 和每一个 $x$ 所对应的决定的。

（我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )）

把 $x$ , $\theta$ , $a$ 分别用矩阵表示：

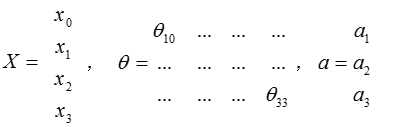
在这里插入图片描述

我们可以得到 $g(\theta \cdot X)=a$ 。

如果细分下去，我们就能够得到向量化的结果：
$g(\Theta^{(1)}\cdot{X^T})=a^{(2)}$

即：

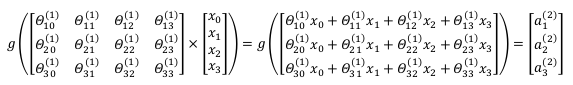
在这里插入图片描述

以上是以第一层为例进行的说明，那么现在我们看第二层，则有
$g(\Theta^{(2)}\cdot a^{(2)})=h_\theta(x)$
我们令 ${z}^( 3 )={\theta }^{( 2 )}{a}^{( 2 )}$ ，则 $h_\theta(x)={a}^{(3)}=g({z}^{(3)})$ 。

更好的理解

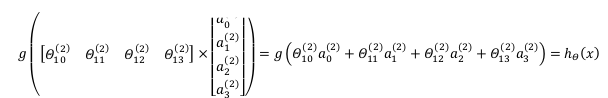
在这里插入图片描述

其实神经网络就像是logistic regression，只不过我们把logistic regression中的输入向量 $[ x_1\sim {x_3} ]$ 变成了中间层的 $[ a_1^{(2)}\sim a_3^{(2)} ]$ ,

即: $h_\theta(x)=g( \Theta_0^{ 2 }a_0^{ 2 }+\Theta_1^{ 2 }a_1^{ 2 }+\Theta_{2}^{ 2 }a_{2}^{ 2 }+\Theta_{3}^{ 2 }a_{3}^{ 2 } )$

我们可以把 $a_0, a_1, a_2, a_3$ 看成更为高级的特征值，也就是 $x_0, x_1, x_2, x_3$ 的进化体，并且它们是由 $x$ 与 $\theta$ 决定的，因为是梯度下降的，所以 $a$ 是变化的，并且变得越来越厉害，所以这些更高级的特征值远比仅仅将 $x$ 次方厉害，也能更好的预测新数据。

这就是神经网络相比于逻辑回归和线性回归的优势。从本质上讲，神经网络能够通过学习得出其自身的一系列特征。在普通的逻辑回归中，我们被限制为使用数据中的原始特征 $x_1,x_2,...,{x}_{n}$ ，我们虽然可以使用一些二项式项来组合这些特征，但是我们仍然受到这些原始特征的限制。在神经网络中，原始特征只是输入层，在我们上面三层的神经网络例子中，第三层也就是输出层做出的预测利用的是第二层的特征，而非输入层中的原始特征，我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征。

单层神经元计算的简化理解

神经网络中，单层神经元（无中间层）的计算可用来表示逻辑运算，比如逻辑与(AND)、逻辑或(OR)。当输入特征为布尔值（0或1）时，我们可以用一个单一的激活层可以作为二元逻辑运算符，为了表示不同的运算符，我们只需要选择不同的权重即可。

在理解之前，我们再复习一下关于激励函数与判定边界。当 $g(z)$ 中 $z > 0$ 时， $g(z)$ > 0.5 ，假如我们的阈值就是 0.5，那么我们此时就把 $g(z)$ 的结果归为 1 ，反之则为 0。

逻辑与

那么，如果我们现在有输出函数 $h_\theta(x) = g(\theta_0x_0+\theta_1x_1+\theta_2x_2)$ ，且 $\Theta = [-30,20,20]$ ，此时 $h_\theta(x) = g(-30+20x_1+20x_2)$ ，我们就能够得到 $x_1x_2$ 分别取值时的结果对照表：

在这里插入图片描述

经过复习和上表的对照我们能够很轻松的理解。

此时 $h_\theta(x)$ 得出的结果等于 $x_1 AND x_2$ 得出的结果，因此我们就能够把此时的输出函数中进行的计算简化理解为：对输入做逻辑与(AND) 运算。

逻辑或

而当 $\Theta = [-10,20,20]$ 时，此时 $h_\theta(x) = g(-10+20x_1+20x_2)$ ，我们就能够得到 $x_1x_2$ 分别取值时的结果对照表：

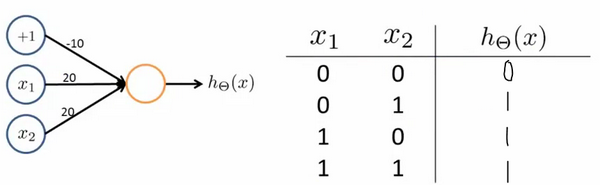
在这里插入图片描述

此时 $h_\theta(x)$ 得出的结果等于 $x_1 OR x_2$ 得出的结果，因此我们就能够把此时的输出函数中进行的计算简化理解为：对输入做 逻辑或(OR) 运算。

逻辑非

当 $\Theta = [10,-20,0]$ 时，此时 $h_\theta(x) = g(10-20x_1)$ ，我们就能够知道 $x_1$ 取 0 时，结果为 1， $x_1$ 取 1 时，结果为 0 。我们就能够把此时的神经元的作用等同于 逻辑非(NOT)

XNOR(输入两个值相等时，结果为 1 )

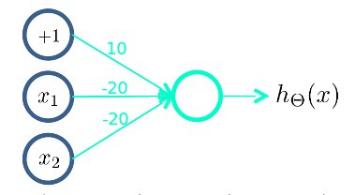
那么我们如何表示呢?

首先我们构造一个能表达 $(NOT x_1) AND (NOTx_2)$ 的神经元进行第一层计算，如图：

在这里插入图片描述

然后构造一个能表示 OR 的神经元进行第二层计算，再让这两层组合在一起：

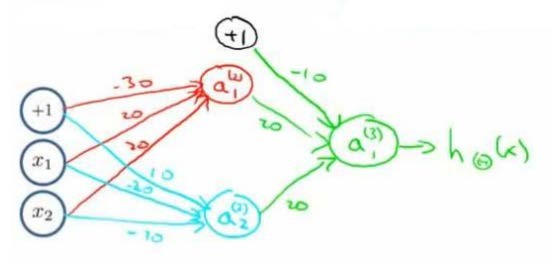
在这里插入图片描述

这样我们就得到了一个能实现 $\text{XNOR}$ 功能的神经网络。

因此，我们能够组合三种简单的运算来逐渐构造出复杂的函数，这样我们也能得到更加复杂有趣的特征值。

这就是神经网络的厉害之处。

多类处理的神经网络

我们在上面的神经网络仅仅输出了一个结果，也就是我们只做了二分类问题，那么我们如果想要进行多个类的分类呢?

很简单，我们只需要让结果值的数目等于你要分类的类数目。比如说：如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车，在输出层我们应该有4个值。第一个值为1或0用于预测是否是行人，第二个值用于判断是否为汽车，第三个值用于预测是否是摩托车，第四个值用于判断是否为卡车。

如果我们构造两个中间层进行，输出层4个神经元分别用来表示4类，那么神经网络图可能如下所示：

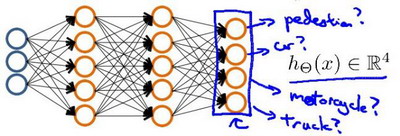
在这里插入图片描述

我们希望当输入人的图片时，输出的结果为 [1 , 0, 0, 0]，输入卡车图片时，输出的结果为 [0 , 0, 0, 1]。

这样，我们就实现了神经网络的多分类处理。

如果对你有所帮助，点个赞吧！

查看更多: https://breezedawn.github.io