机器学习 - 深度学习 - 神经网络

深度学习背景引入

和机器学习的关系对比

机器学习是很大的一个范围, 包好了深度学习在内的很多内容

卷积神经网络又是深度学习中的一个特化的子类

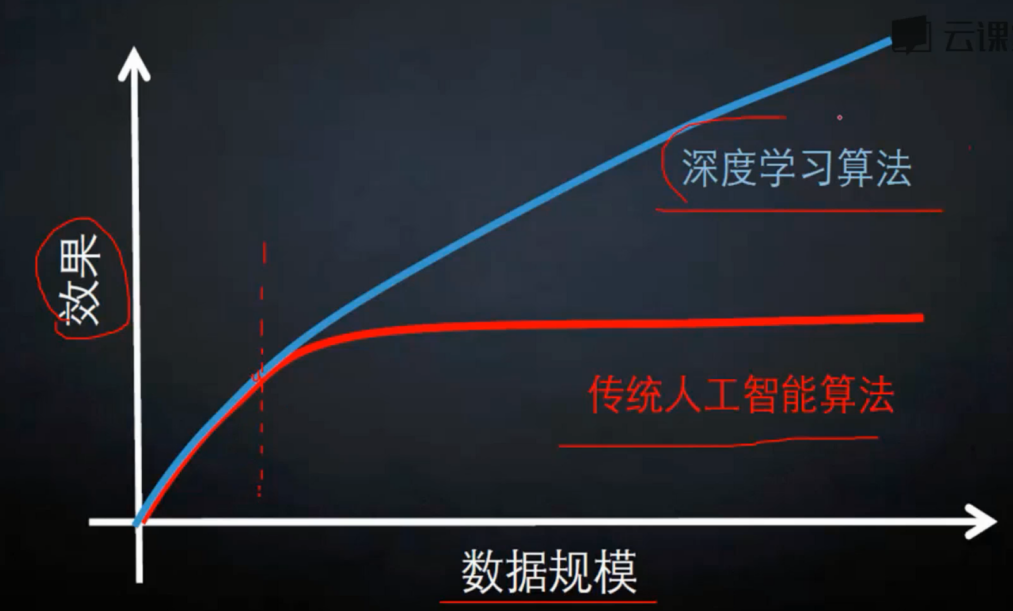
在数据量不大的程度下, 深度学习和传统的人工智能算法没有太大的区别

但是上限方面就要高得多, 而且数据规模越大差距越大

计算机视觉

深度学习和计算机视觉几乎是绑定的, 很多深度学习的实际应用都脱离不了计算机视觉

图形读取

图像由三维数组形式, 每个像素点的值 0-255 表示亮度

例如 300*100*3 这种格式 表示长 300 宽100, 颜色通道 3

通常颜色通道都是由 RGB 三原色通道 组成

识别挑战

角度, 采光, 形状的变化以及部分遮蔽,背景混入都会加大识别的难度

 

常规套路

收集数据并给定标签

训练分类器

测试评估

K - 近邻算法

原理概述

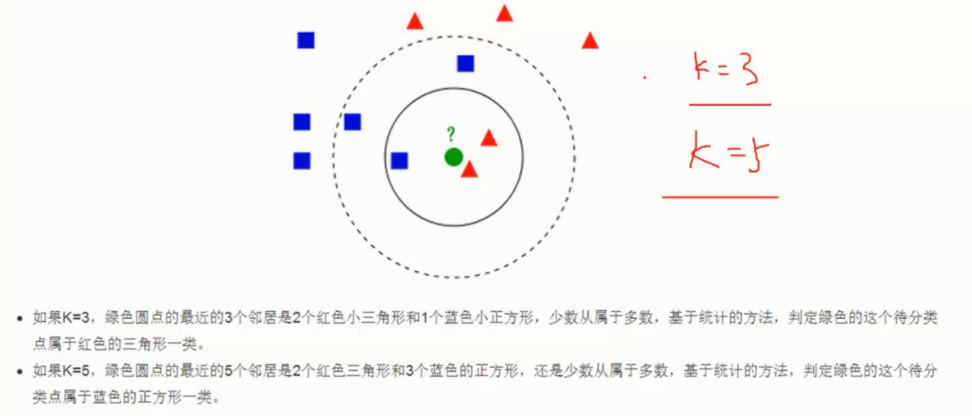
工作流程

距离计算

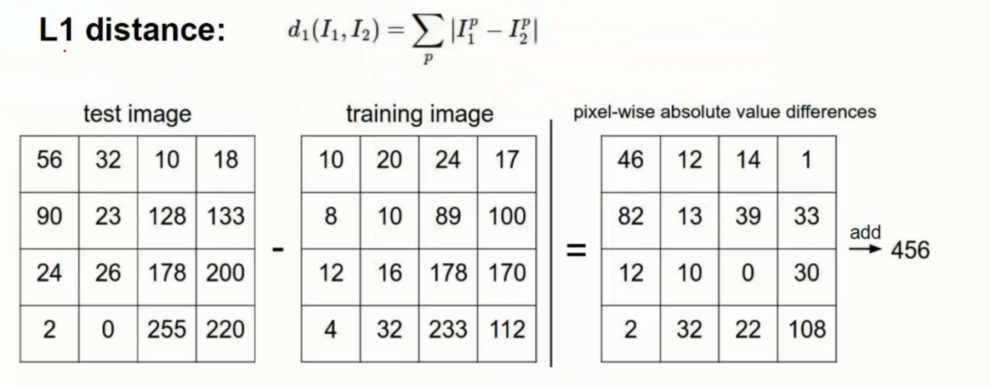
首先需要计算的就是当前点到所有点之间的距离

这里的计算方式是直接用对应相同位置像素点直接运算计算差异后求和即可得出距离

这么简单的运算当然结果并不理想, 得出的结果可以说相当的糟糕

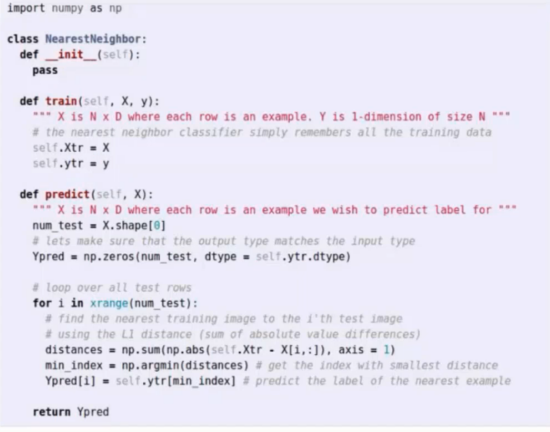
代码

超参数

上面的 K - 近邻 算法中所用的 L1 距离计算作为参数也被称作超参数

即可以使用 L1 参数也可以使用 L2 参数

参数选择思考

距离如何设定? 是选择 L1还是 L2?

对于K 近邻的 K 怎么选择?

入股有其他超参数该如何设定? 

参数的选择还是需要通过多次的测试数据试验, 找到最好的一组参数组合 ? 

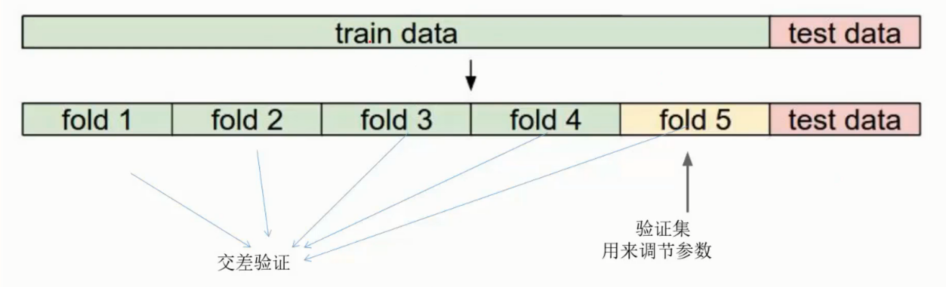
　　测试集是宝贵的, 测试集只能最终使用,

　　参数调节应该在此步骤之前做好, 不应该再用测试集来进行参数选择

引入交叉验证从而解决这个问题

背景主导

在 使用 K - 近邻的时候是对所有的像素点的相同位置进行距离计算, 是包括到了背景内容的

分类是基于图形中的主体就会导致较大的误差

不同的变换和原图具有相同的 L2 距离, 因此 K 近邻算法基本上完全不可取

算法总结

 在上述的原理和特殊场景中, 可以看到 K - 近邻的算法存在很大的计算问题导致的短板

因此实际工作不会使用, 这里是为了便于对比理解使用的负面教材

线性分类

引例 - 识别猫图

对于一张 32*32*3 的图片进行识别的的算法逻辑, 输入 x 表示图片数据, W 表示一系列参数

最终的目的是获得一个较高的期望的分这里假设就是对1-10 分类的判断

已知输入

32*32*3 = 3072 ,输入数据进行拉伸成一个一维的数组内含有 3073 个像素点的信息数据即 x 

可以视为一个 长度 3072 * 1 的列向量

已知输出

得出的结果我们期望是一个 10 * 1 的列矩阵, 表示每一行都是分别 分类 1-10 的期望值

最终的结果在此 10 分类中取结果最高值

未知输入

这里已知输入 x 和 输出之后, 如何确定参数  W 

W 需要具备一个能力 - 即将 3072*1 转变为 10*1 的能力

因此 W 必然是 10 * 3072 的行向量

计算

如上图是假设这个猫图是4像素点, x 是 4 *1 的输入, 则 W 参数则需要 3 * 4 的输入, 

而且 W 的参数存在很小也很大,  表示是此像素点(特征)更大或更小得要影响, 正负则表示是积极/消极影响

最终得出的结果为 -96.8 认为是猫, 437.9 认为是狗 61.95 认为是船, 因此被认为是狗了.

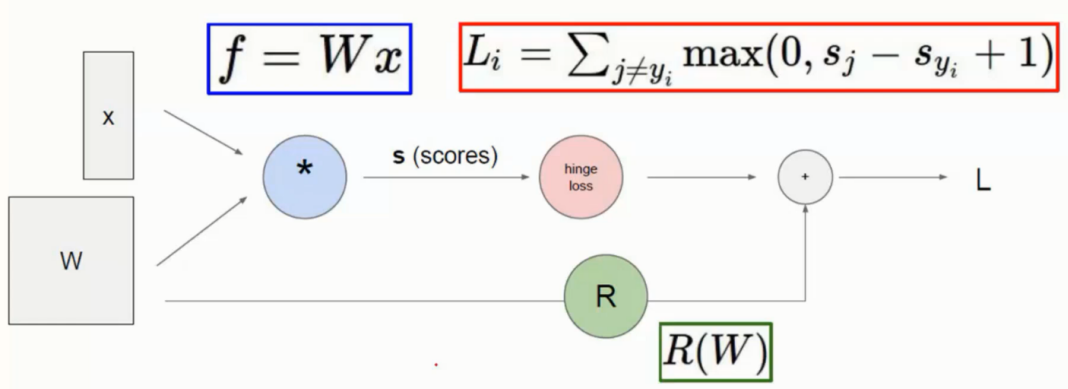
损失函数

损失函数是将预测错误的所有情况的得分与正确的相减后, 如果小于 0 就当 0 处理

然后最终累加起来的数值则为损失值

损失值越大则表示预测的约不准

损失函数的这里的式子中的 +1 可以作为参数指定, 即下图中的 delta 即可划分正确错误之间的界限区间

最终是需要将所有的损失值进行累加的, 然后取平均值刨除样本个数的影响从而实现对整个模型的评估

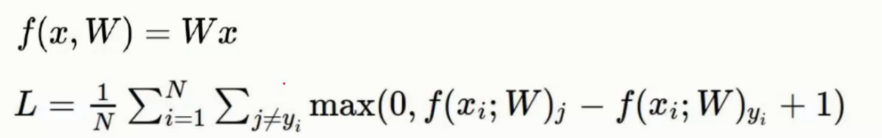
正则化惩罚

如图的 w1 模型参数为 [1,0,0,0] 而 w2 模型参数 [0.25,0.25,0.25,0.25]

很明显两个模型参数不同是不一样的模型, 但是如果在 x 输入为 [1,1,1,1] 的时候

得出的结果最终结果同样是 1 

按照直观的分析 , w1 模型最对首个数据有侧重计算, 其他都为 0 了

而 w2 则对每一个数据都有计算从而更加囊括覆盖, 很明显优于 会有过拟合风险的 w1 模型

这种场景的处理则需要使用正则化惩罚

在之前的损失函数的式子上加入了正则化惩罚项

 结合上面的示例中, w1 的惩罚值就是 1, 而 w2 的惩罚值为 0.25 明显小于 w1, 因此 w1 的惩罚更重一些

于是将 w1 和 w2 的结果进行了区分, 从而让我们能够选择 w2 模型

最终公式

最终的终极版公式则如下

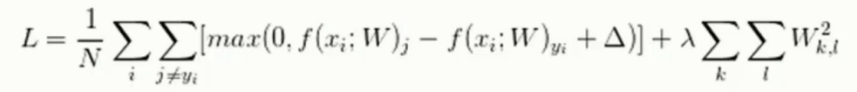
最终的结果始终是个分值, 是可以求得解的一个具体的数字

softmax 分类器

对于一个分类的操作, 一个数值的结果是没办法分类的

像是线性回归以及 SVM 都是得出一个具体的值

而 softmax 输出的则是概率

原理

sigmoid 函数

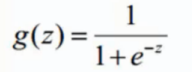 输入区间为 [+ ∞ , - ∞] , 输出区间为 (0,1)

softmax 函数

softmax 函数的输出 ( 归一化的分类概率 )

损失函数 :  交叉熵损失

输入的值为一个向量, 向量中元素为任意实数的评分值

输出的为一个向量, 其中每个元素值在 0-1 之间, 且所有元素之和 为 1 

举例

对上面线性得出的结果进行一个 exp 的映射操作将数据放大, 然后进行归一化操作从而得出概率值

这里判断是猫的概率只有 13%, 判断是汽车的概率是 87%

exp:

　　会将本来就较大的数值更大, 将本来就小的数值体现的更小

归一化操作:

　　比如 1, 2, 3 转换为 1/6, 2/6, 3/6 即可

损失函数使用的是 -log的形式来进行判断, 根绝得出的值越大则表示越不准确

损失函数对比

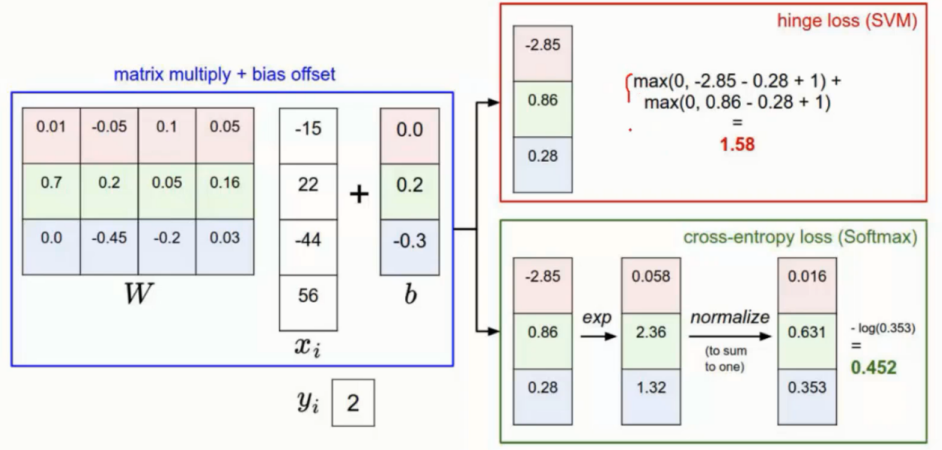
由此可见 exp 的处理后更加合适

最优化

Bachsize

通常为 2 的整数倍, 根据计算机性能来决定

指定 每次前向传播反向传播的数据量

Epoch

整个数据集的重复次数, 即对所有数据的迭代一次才算一次 epoch

和 bachsize 是完全不同的概念

前向/反向传播概念

结合上面的的公式过程就是如上图所示

从开始输入参数, 然后得到损失值 这样的一次过程就叫做前向传播

然后用过前向传播得到的结果, 我们在反向传播从而优化输入参数 W 

反向传播求解

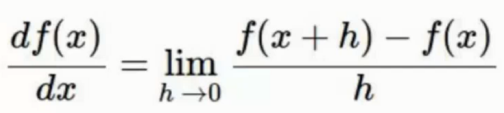
 这里使用的方法就是梯度下降方法, 利用每个点的坡度(求导) 这样找到最快的下降方向求解

从而让 w 通过每次的迭代更加接近于最低谷最优解

示例

上图中

先把 q = x+y 取出来

对 z 求导数为 f(x) = qz 即 导数为 q = 3  

对 x  求导数首先要对 q 求导

对 q 求导数为 f(x) = qz 即 导数为 z = -4

对 x , y 求导 则为 q = x + y 

x 对 q 的导数 为  1

根据链式法则, 这里的 x 对 f(x) 的导数相乘 即 1* (-4)  = -4

 

较为复杂的函数示例如上

 整体求导更加便捷, 以及根据求导的基本法则可以进行一系列简单的判断,如下面的三种最常见的门单元

学习率

 

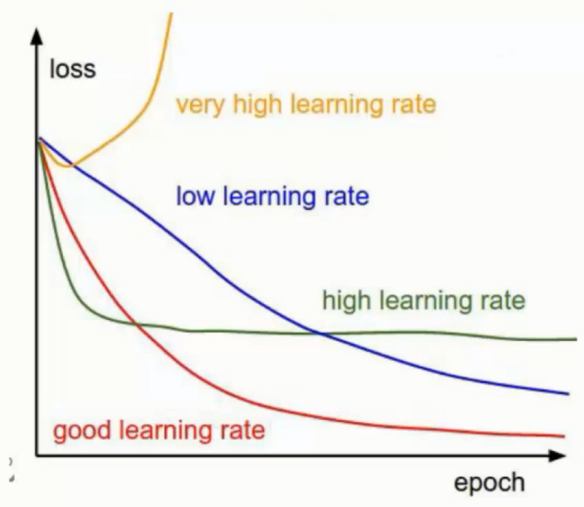
最优化问题的目的是求解 W , 每次对 W 都会有更新记作 ΔW  = W2 - W1

 然后更新 W 的时候对 ΔW 再乘个学习率在做更新, 即不一次更新全部

学习率的改变是对模型影响相当大的, 一般会设置很小, 然后通过大量的迭代次数来优化

这样可以防止学习率过大出现如下图这种情况

 

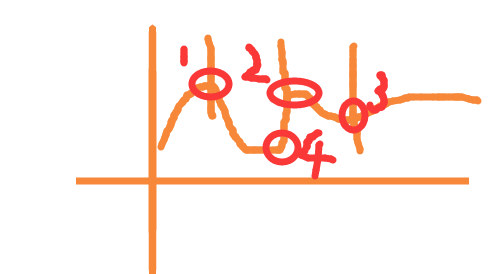
从1到2再到3, 因为学习率太大所以 真正的最低点 4 就被跳过了

 代码中的体现

神经网络

 以上的全部的就已经是神经网络的全部组件了. 需要进行拼凑即可

结构

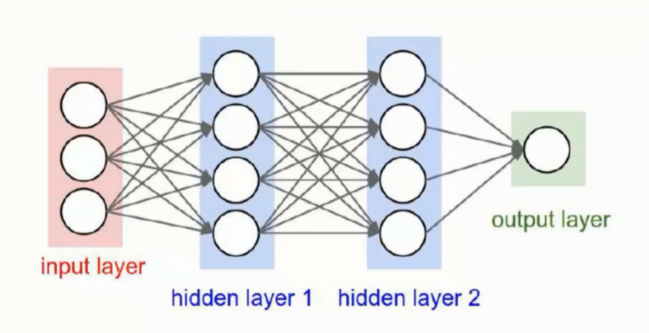
神经元

按照图形中的画法其实感觉是每个圈圈都是一个类似 神经元 的结构体 - 后面姑且就叫神经元了

神经元的数量会直接影响到模型的最终预测结果

但是过多的神经元也会造成过拟合的风险

越多的神经元越能够表达更复杂的模型

举例 一个神经元那就是一条线性

两个神经元就会两个线性

三个神经元会形成三角形

四个神经元就会形成四边形这样类似的堆叠下去最终进行划分

流传过程

神经元其实是每次的 W 的参数调整的一次前后向传播

前一轮的结果作为后一轮的输入继续传递下去

公式的话就类似于 f(x) =  w3 * [w2 *  (w1x1) ] 这样的过程 

就是由 权重参数 的组合最终得到结果

激活函数

神经网络中的线性表达无法实现效果的时候

需要使用激活函数进行包装转变为非线性

Sigmoid 函数

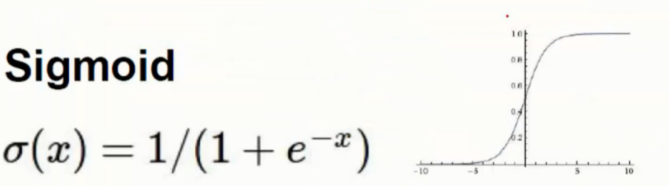
Sigmoid 函数本身就是曲线的

加入激活函数后就可以进行一定程度的弯曲处理

而后 Sigmoid 函数被取代　-  原因: 梯度消失现象

Sigmoid  函数的图形中可以看出例如在 5 之后的数值其梯度就逐渐接近于 0 

而神经网络的多层级结构需要对梯度下降的时候是累乘处理

而越大的数值在 Sigmoid  函数中的梯度则越小, 最终累乘后悔逐渐趋于 0 

无法再继续为模型进行优化迭代了, 越是层级较高的神经网络, 梯度消失现象就越加剧

ReLU 函数

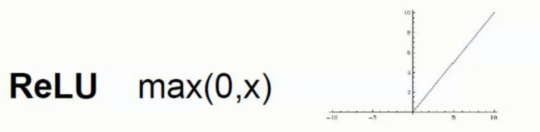
ReLU 激活函数则就简单的多, 本身的梯度都是一样的, 因此不会出现梯度消失现象, 而且求导也容易

目前来说是神经网络或者卷积神经网络都是首选的是 ReLU 函数作为激活函数

公式

线性返程

非线性方程

单层的神经网络

 

双层的神经网络

更为详细的图示

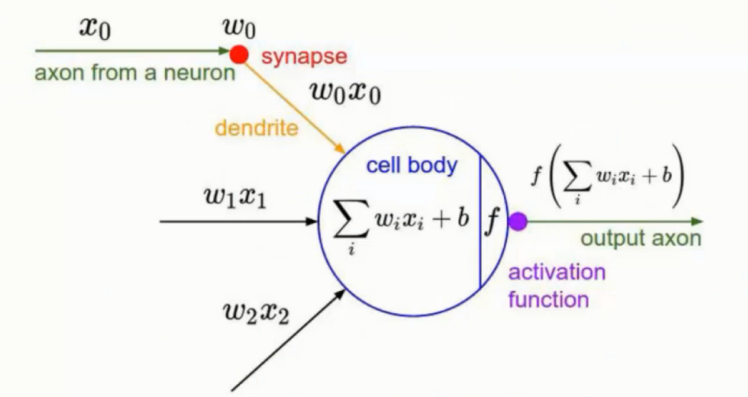
正则化项

为了解决过拟合问题

λw² 項引入可以让神经网络模型泛化能力更强

数据预处理

首先要将标准对其到 0 , 即以 0 作为基准 - 所有的数据减去平均值即可到达 0 基准位置

然后 除以标准差将各个特征的数值进行对其

权重初始化

神经网络的层及结构是累乘的处理

因此使用 全 0 的初始值是无意义的

但是如果使用全 1, 或者全 2 这样的固定值也只会让他向同一方向去收敛, 效率低下

因此最佳的策略是使用随机初始化或者高斯初始化

至于 b 则是可以用 全 0 或者 全 1 初始化皆可

DROP-OUT

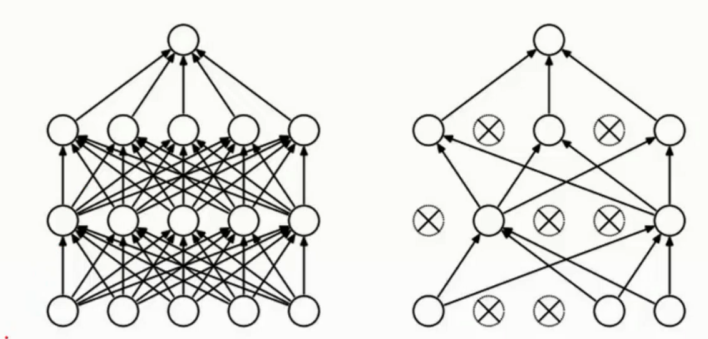
神经元使用全链接进行操作的话, 结构较为复杂, 且容易过拟合

因此还是基于随机的选择部分的 神经元被 弃用, 不使用弃用的神经元进行更新

但是弃用至是一次性的, 即每次是完全随机的选择某些神经元被弃用

这样稍微削减一些神经网络的大小, 不再过分臃肿

代码实现神经网络

原始数据集

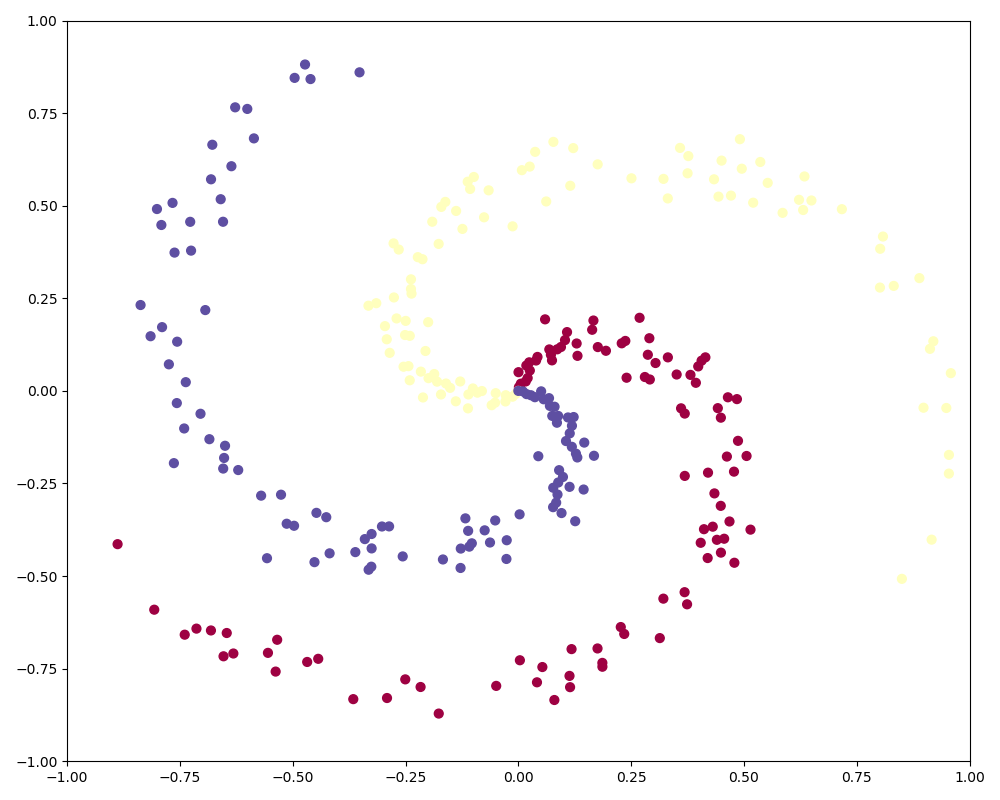
import numpy as np
import matplotlib.pyplot as plt

# ubuntu 16.04 sudo pip instal matplotlib

plt.rcParams['figure.figsize'] = (10.0, 8.0)  # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

np.random.seed(0)
N = 100  # number of points per class
D = 2  # dimensionality
K = 3  # number of classes
X = np.zeros((N * K, D))
y = np.zeros(N * K, dtype='uint8')
for j in range(K):
    ix = range(N * j, N * (j + 1))
    r = np.linspace(0.0, 1, N)  # radius
    t = np.linspace(j * 4, (j + 1) * 4, N) + np.random.randn(N) * 0.2  # theta
    X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
    y[ix] = j
fig = plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim([-1, 1])
plt.ylim([-1, 1])
plt.show()

绘制一个三种分类, 然后每个分类 100 个点的环形围绕的图形

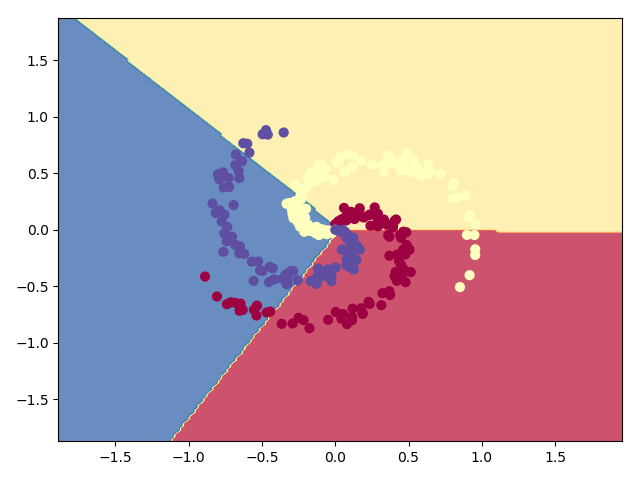
普通的线性分类

# Train a Linear Classifier
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
N = 100  # number of points per class
D = 2  # dimensionality
K = 3  # number of classes
X = np.zeros((N * K, D))
y = np.zeros(N * K, dtype='uint8')
for j in range(K):
    ix = range(N * j, N * (j + 1))
    r = np.linspace(0.0, 1, N)  # radius
    t = np.linspace(j * 4, (j + 1) * 4, N) + np.random.randn(N) * 0.2  # theta
    X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
    y[ix] = j

W = 0.01 * np.random.randn(D, K)
b = np.zeros((1, K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3  # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(1000):
    # print X.shape
    # evaluate class scores, [N x K]
    scores = np.dot(X, W) + b  # x:300*2 scores:300*3
    # print scores.shape
    # compute the class probabilities
    exp_scores = np.exp(scores)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)  # [N x K] probs:300*3
    print(probs.shape)

    # compute the loss: average cross-entropy loss and regularization
    corect_logprobs = -np.log(probs[range(num_examples), y])  # corect_logprobs:300*1
    print(corect_logprobs.shape)

    data_loss = np.sum(corect_logprobs) / num_examples
    reg_loss = 0.5 * reg * np.sum(W * W)
    loss = data_loss + reg_loss
    if i % 100 == 0:
        print("iteration %d: loss %f" % (i, loss))

    # compute the gradient on scores
    dscores = probs
    dscores[range(num_examples), y] -= 1
    dscores /= num_examples

    # backpropate the gradient to the parameters (W,b)
    dW = np.dot(X.T, dscores)
    db = np.sum(dscores, axis=0, keepdims=True)

    dW += reg * W  # regularization gradient

    # perform a parameter update
    W += -step_size * dW
    b += -step_size * db
    scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))

h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

结果

线性的划分无论如何在环装的数据集上都没办法表现出来

使用神经网络

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
N = 100  # number of points per class
D = 2  # dimensionality
K = 3  # number of classes
X = np.zeros((N * K, D))
y = np.zeros(N * K, dtype='uint8')
for j in range(K):
    ix = range(N * j, N * (j + 1))
    r = np.linspace(0.0, 1, N)  # radius
    t = np.linspace(j * 4, (j + 1) * 4, N) + np.random.randn(N) * 0.2  # theta
    X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
    y[ix] = j

h = 100  # size of hidden layer
W = 0.01 * np.random.randn(D, h)  # x:300*2  2*100
b = np.zeros((1, h))
W2 = 0.01 * np.random.randn(h, K)
b2 = np.zeros((1, K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3  # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(2000):

    # evaluate class scores, [N x K]
    hidden_layer = np.maximum(0, np.dot(X, W) + b)  # note, ReLU activation hidden_layer:300*100
    # print hidden_layer.shape
    scores = np.dot(hidden_layer, W2) + b2  # scores:300*3
    # print scores.shape
    # compute the class probabilities
    exp_scores = np.exp(scores)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)  # [N x K]
    # print probs.shape

    # compute the loss: average cross-entropy loss and regularization
    corect_logprobs = -np.log(probs[range(num_examples), y])
    data_loss = np.sum(corect_logprobs) / num_examples
    reg_loss = 0.5 * reg * np.sum(W * W) + 0.5 * reg * np.sum(W2 * W2)
    loss = data_loss + reg_loss
    if i % 100 == 0:
        print("iteration %d: loss %f" % (i, loss))

    # compute the gradient on scores
    dscores = probs
    dscores[range(num_examples), y] -= 1
    dscores /= num_examples

    # backpropate the gradient to the parameters
    # first backprop into parameters W2 and b2
    dW2 = np.dot(hidden_layer.T, dscores)
    db2 = np.sum(dscores, axis=0, keepdims=True)
    # next backprop into hidden layer
    dhidden = np.dot(dscores, W2.T)
    # backprop the ReLU non-linearity
    dhidden[hidden_layer <= 0] = 0
    # finally into W,b
    dW = np.dot(X.T, dhidden)
    db = np.sum(dhidden, axis=0, keepdims=True)

    # add regularization gradient contribution
    dW2 += reg * W2
    dW += reg * W

    # perform a parameter update
    W += -step_size * dW
    b += -step_size * db
    W2 += -step_size * dW2
    b2 += -step_size * db2
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))

h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.maximum(0, np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b), W2) + b2
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

结果

收敛的次数在 1200 次的时候 loss 基本变化不大了

iteration 0: loss 1.098765
iteration 100: loss 0.723927
iteration 200: loss 0.697608
iteration 300: loss 0.587562
iteration 400: loss 0.426585
iteration 500: loss 0.357190
iteration 600: loss 0.349933
iteration 700: loss 0.346522
iteration 800: loss 0.336137
iteration 900: loss 0.309860
iteration 1000: loss 0.292278
iteration 1100: loss 0.284574
iteration 1200: loss 0.275849
iteration 1300: loss 0.271355
iteration 1400: loss 0.267756
iteration 1500: loss 0.265369
iteration 1600: loss 0.262948
iteration 1700: loss 0.260838
iteration 1800: loss 0.259226
iteration 1900: loss 0.257831
training accuracy: 0.97