【上一篇 3 有限马尔可夫决策过程（Finite Markov Decision Processes）】【下一篇 5 蒙特卡洛方法（Monte Carlo Method）】

之前介绍的知识都是基础，从这次开始才真正开始介绍增强学习的解法方法。
　　动态编程（Dynamic Programming, DP）这个词大家肯定都不陌生，在解决算法编程问题当中经常会用到，它的主要思想就是将一个复杂的问题分解成多个子问题，将子问题的解结合在一起就构成了原问题的解，它常常适合于解决具有如下两种属性的问题：
　　（1）优化的子结构：优化解常常可以分解成子问题；
　　（2）子问题有重叠：即子问题总是重复出现，该子问题的解可以保存下来重复利用。
　　
　　而马尔可夫决策过程就完美的符合这两点特性：
　　（1）需要求解的 Bellman 方程提供了递归的分解形式；
　　（2）Value function 需要存储和重用之前的解。

因此可以说 DP 可以用于求解马尔可夫模型的优化策略，但是由于 DP 问题需要环境的动态模型，并且计算复杂度较高，因此在增强学习中的应用并不广泛，但是它的思想在理论上还是非常重要的，是以后学习的一个理论基础。DP 算法的主要思想就是利用 value function 来寻找好的策略。
　　
　　这里先介绍一下后文中的符号表示（与之前的相同）：
　　假设状态集合、行为集合和 reward 集合分别为 $\mathcal{S}$ 、 $\mathcal{A}(s)$ 和 $\mathcal{R}$ ，动态性用概率 $p(s’,r|s,a)$ 来表示，其中 $s\in\mathcal{S}$ 、 $a\in\mathcal{A}(s)$ 、 $r\in\mathcal{R}$ 、 $s’\in\mathcal{S}^+$ （若问题为 episodic，则 $\mathcal{S}^+$ 指的是 $\mathcal{S}$ 加上终止状态）。
　　之前介绍过，若找到了满足 Bellman 优化方程的优化值函数 $v_*$ 或者 $q_*$ ，就可以容易的获得优化的策略， $v_*$ 与 $q_*$ 的表达式如下所示：
$\begin{aligned} v_{\ast}(s) &= max_a{\Bbb E}[R_{t+1}+\gamma v_{\ast}(S_{t+1})|S_t=s,A_t=a] \\ &= max_a\sum_{s’,r}{p(s’,r|s,a)[r+\gamma v_{\ast}(s’)]} \end{aligned}$

$\begin{aligned} q_{\ast}(s,a) &= {\Bbb E}[R_{t+1}+\gamma max_{a’}q_{\ast}(S_{t+1},a’) |S_t=s, A_t=a] \\ &= \sum_{s’,r}{p(s’,r|s,a)[r+\gamma max_{a’}q_{\ast}(s’,a’)]} \end{aligned}$

1、Policy Evaluation

在DP中， $policy\ evaluation$ 指的是对任意规则 $\pi$ 计算 state-value 函数 $v_{\pi}$ ，也可以将这个称作是预测问题（ $prediction\ problem$ ）。在上一节的内容中提到 $s\in\mathcal{S}$ 都有
$\begin{aligned} v_{\pi}(s) &\doteq {\Bbb E}_{\pi}[R_{t+1}+\gamma R_{t+2}+\gamma ^2 R_{t+3}+\cdots | S_t=s] \\ &= {\Bbb E}_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})| S_t=s] \\ &=\sum_a{\pi(a|s)}\sum_{s’,r}{p(s’,r|s,a)[r+\gamma v_{\pi}(s’)]} \end{aligned}$

从最后一个式子中可以看出， $v_{\pi}(s)$ 的计算还要依赖于 $v_{\pi}(s’)$ ，对于这种情况，最常用的方法采用迭代的形式，不断地更新和逼近真实值。这里可以考虑一个近似的值函数序列 $v_0,v_1,v_2,\cdots$ ，其中每个值函数都是从 $\mathcal{S}^+$ 向 ${\Bbb R}$ 的映射，其中初始的近似值 $v_0$ 是任意选择的（终止状态的值为 0），之后的计算都是利用 $v_{\pi}$ 的 Bellman 方程来进行更新的：
$\begin{aligned} v_{k+1}(s) &\doteq {\Bbb E}_{\pi}[R_{t+1}+\gamma v_{k}(S_{t+1})| S_t=s] \\ &=\sum_a{\pi(a|s)}\sum_{s’,r}{p(s’,r|s,a)[r+\gamma v_{k}(s’)]} \end{aligned}$

当 $k \rightarrow \infty$ 时，序列 $\{v_k\}$ 会收敛于 $v_{\pi}$ ，这个算法就称为是 $iterative \ policy \ evaluation$ 。整个过程可以描述为:
　　 $v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_{\pi}$
　　为了从 $v_k$ 得到近似的 $v_{k+1}$ ，iterative policy evaluation 需要对每一个状态 $s$ 做同样的操作：将 $s$ 旧的 value 值换成计算得到的新的 value 值，将这种操作可以称为是 $full \ backup$ ，迭代策略评估的每一次迭代过程都需要把每个状态的 value 备份起来。
　　迭代算法常用的停止准则是检测最大的状态变化量，整个过程的伪代码如下：

2、Policy Improvement

第一节中是计算每个 policy 的 value function，它的目的当然是为了找到更好的 policies，假设我们已经有了某个 $\pi$ 的值函数 $v_{\pi}$ ，那我们肯定想知道是否可以通过对规则 $\pi$ 改进来得到更好的规则，改进的方式就是在改变在某个状态时的行为选择概率，即 $a=\pi(s)$ ，我们肯定会想，在状态 $s$ 时，我们依据当前的 $v_{\pi}(s)$ 到底是好还是不好呢？是否可以改进呢？那我们可以采用比较 $q_{\pi}(s,a)$ 与 $v_{\pi}(s)$ 的方法，若 $q_{\pi}(s,a)$ 比 $v_{\pi}(s)$ 大，那么采用“在状态 $s$ 时选择行为 $a$ ，之后还遵从规则 $\pi$ ”就要比“无论什么状态下都遵从规则 $\pi$ ”要好。
　　
　　通常将这种理论称为是 $policy \ improvement \ theorem$ ，假设一对任意的规则 $\pi$ 与 $\pi ’$ ，若对所有的 $s\in\mathcal{S}$ 都有：
$q_{\pi}(s,\pi’(s)) \geq v_{\pi}(s)$
　　那么规则 $\pi ’$ 一定比规则 $\pi$ 更好或者相当，也就是说，对所有的状态 $s\in\mathcal{S}$ 它的期望返回值都要高或者相当：
$v_{\pi’}(s) \geq v_{\pi}(s)$
　　回到我们之前的问题，我们如何对规则 $\pi$ 进行改进呢？这里假设规则 $\pi$ 是原始的规则，规则 $\pi ’$ 是改进后的规则，这两个规则只有在 $\pi’(s)=a \neq \pi(s)$ 不同，其他地方完全相同，若我们知道 $q_{\pi}(s,a)> v_{\pi}(s)$ ，那我们就可以知道规则 $\pi$ 比规则 $\pi$ 要好，它的证明过程如下：

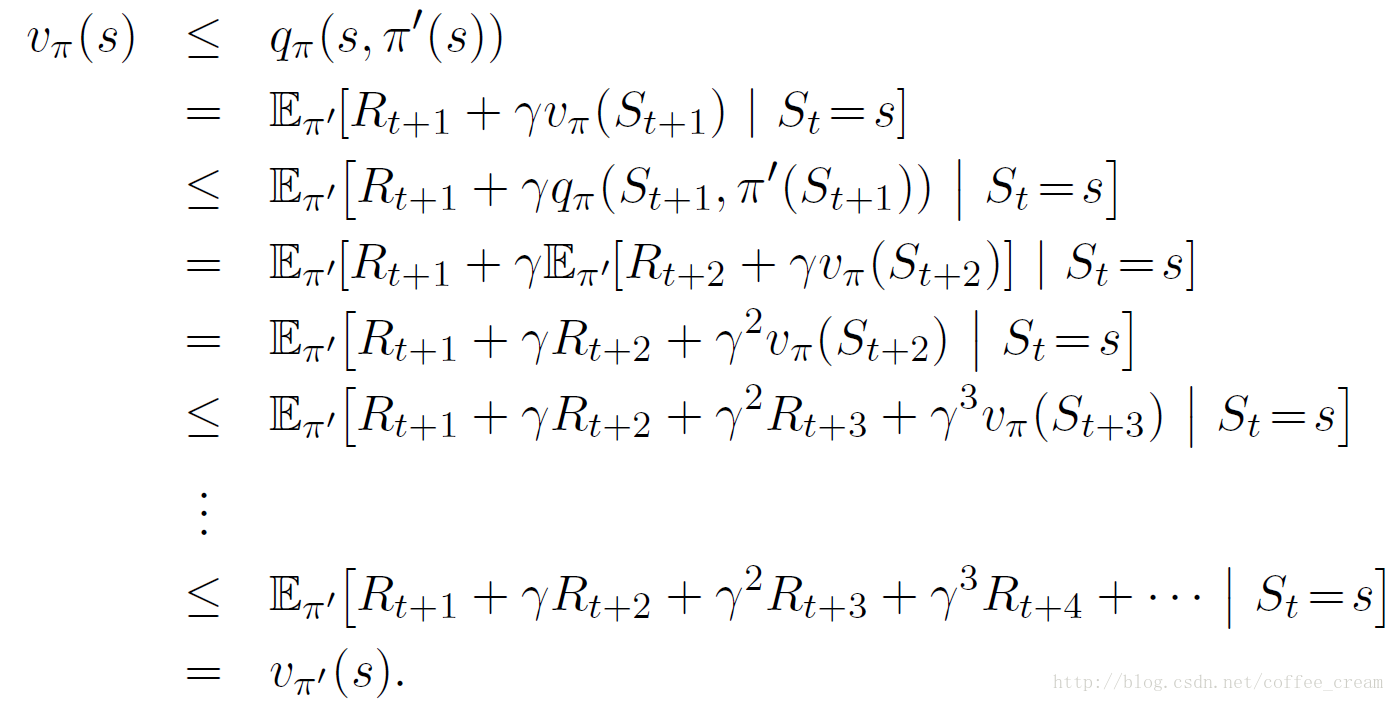
从中可以看出，只要改善一个状态的行为就可以对规则进行改进，自然而然地肯定会想，如果把所有的状态都改成可能的最好行为，那得到的规则会很好，也就是这样的一个 $greedy$ 规则 $\pi$ ：
$\begin{aligned} {\pi}'(s) &\doteq argmax_a{q_{\pi}(s,a)} \\ &= argmax_a {\Bbb E} [R_{t+1}+\gamma v_{\pi}(S_{t+1})| S_t=s,A_t=a] \ \ \ \ \ \ \ (1)\\ &= argmax_a \sum_{s’,r}p(s’,r|s,a)[r+\gamma v_{\pi}(s’)] \end{aligned}$

其中 $argmax_a$ 指的是选择使后面式子最大的行为 $a$ 。
　　这种贪婪的规则依据 $v_{\pi}$ 选择短期内最好的行为，从结构上看，这种贪婪的规则满足 policy improvement theorem，因此比原始的规则要好，因此将这个过程就称为是 $policy \ improvement$ 。
　　假设这个贪婪的规则 $\pi’$ 并不比规则 $\pi$ 好，而是两者相当，则 $v_{\pi}= v_{\pi’}$ ，则根据公式（1）有：
$\begin{aligned} v_{\pi’}(s) &= max_a {\Bbb E} [R_{t+1}+\gamma v_{\pi’}(S_{t+1})| S_t=s,A_t=a] \\ &= max_a \sum_{s’,r}p(s’,r|s,a)[r+\gamma v_{\pi’}(s’)] \end{aligned}$

这个方程与 Bellman 优化方程相同，因此 $v_{\pi’}(s)$ 一定是 $v_{\ast}$ ，因此规则 $\pi’$ 与规则 $\pi$ 一定都是 optimal policies。因此，除非该规则已经是 optimal policies，否则 policy improvement 过程一定会给出一个严格更好的规则。

3、Policy Iteration

第一节介绍的是规则评价，第二节是规则改善，这里要将前两节结合到一起，从而得到下面的过程：
$\pi_0 \xrightarrow{E} v_{\pi_0} \xrightarrow{I} \pi_1 \xrightarrow{E} v_{\pi_1} \xrightarrow{I} \pi_2 \xrightarrow{E} \cdots \xrightarrow{I} \pi_{\ast} \xrightarrow{E} v_{\pi_{\ast}}$
　　其中， $\xrightarrow{E}$ 代表的是 policy evaluation， $\xrightarrow{I}$ 代表的是 policy improvement，并且该 improvement 保证是严格的提升。因为有限 MDP 只含有有限的规则，因此该过程最终一定会收敛到 optimal policy。这种查询过程就称为是 $policy \ iteration$ ，完整的伪代码如下所示：

4、Value Iteration

Policy iteration 的一个缺点是在每次迭代中都要进行 policy evaluation，这个过程是非常耗时的，事实上该过程是可以缩短的，并且不会影响收敛，其中一种重要的方法就是 $value iteration$ ，它可以写作是一个结合了 policy improvement 和删减的 policy evaluation 步骤的简单备份操作：
　　
$\begin{aligned} v_{k+1}(s) &\doteq max_a {\Bbb E} [R_{t+1}+\gamma v_{k}(S_{t+1})| S_t=s,A_t=a] \\ &= max_a \sum_{s’,r}p(s’,r|s,a)[r+\gamma v_{k}(s’)] \end{aligned}$

对任意的 $v_0$ ，序列 $\{v_k\}$ 最终都可以收敛到 $v_{\ast}$ 。
　　
　　算法的伪代码如下：

所有的 truncated policy iteration 算法都可以视为是 $sweep$ 序列，其中一些使用的是 policy evaluation backups，另一些使用的是 value iteration backups。

5、Asynchronous Dynamic Programming 异步的动态编程

DP方法的一个主要缺点就是在于它需要遍历 MDP 过程的整个状态集合，即需要对 state set 进行 sweep，当状态集合很大时，一次 sweep 就需要耗费巨大。
　　Asynchronous DP 方法替代了 iterative DP 算法，不是对状态集的系统地 sweep，这些方法会以任何顺序备份状态的 values，一些状态的 values 还有可能在其他状态第一次备份之前就备份了很多次。但为了正确收敛，异步算法必须继续备份所有的 values，异步 DP 在选择状态方面提供了很大的自由度。

6、Generalized Policy Iteration

广义的 policy iteration 可以用下图来表示：

Policy iteration 其实就是由两个连续的交互过程构成的：policy evaluation 和 policy improvement，在异步 DP 方法中，这两个过程是交错的。
　　这里用 Generalized Policy Iteration （GPI）来代表这种一般化的思想，几乎所有的增强学习方法都可以描述为 GPI。在 GPI 中，policy evaluation 和 policy improvement 既是竞争的也是合作的。
　　
　　
　　
参考文献
[1] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto
[2] UCL Course on RL

4 动态编程（Dynamic Programming, DP）