谈到傅立叶变换,必然离不开基本的无穷级数。无穷级数是高等数学的一个重要组成部分,它是表示函数,研究函数性质的以及进行数值计算的一种工具,本文先讨论常数项级数,接着讨论函数的幂级数,然后讨论函数的三角幂级数分解,最后到傅立叶级数然后到傅立叶变换。在介绍傅立叶变换时,会结合数学和物理,自然常识,尽量做到深入浅出。
本文将按照以下篇幅进行论述:
一、常数项级数以及幂级数
二、函数的幂级数展开
三、傅立叶级数
四、傅立叶变换
1 常数项级数以及幂级数
这部分将以圆的面积作为切入点。
在古代祖冲之就已经推算出了圆周率,用的是无限分割法,割之再割,不能再割。

幂级数的收敛,以指数函数为例:
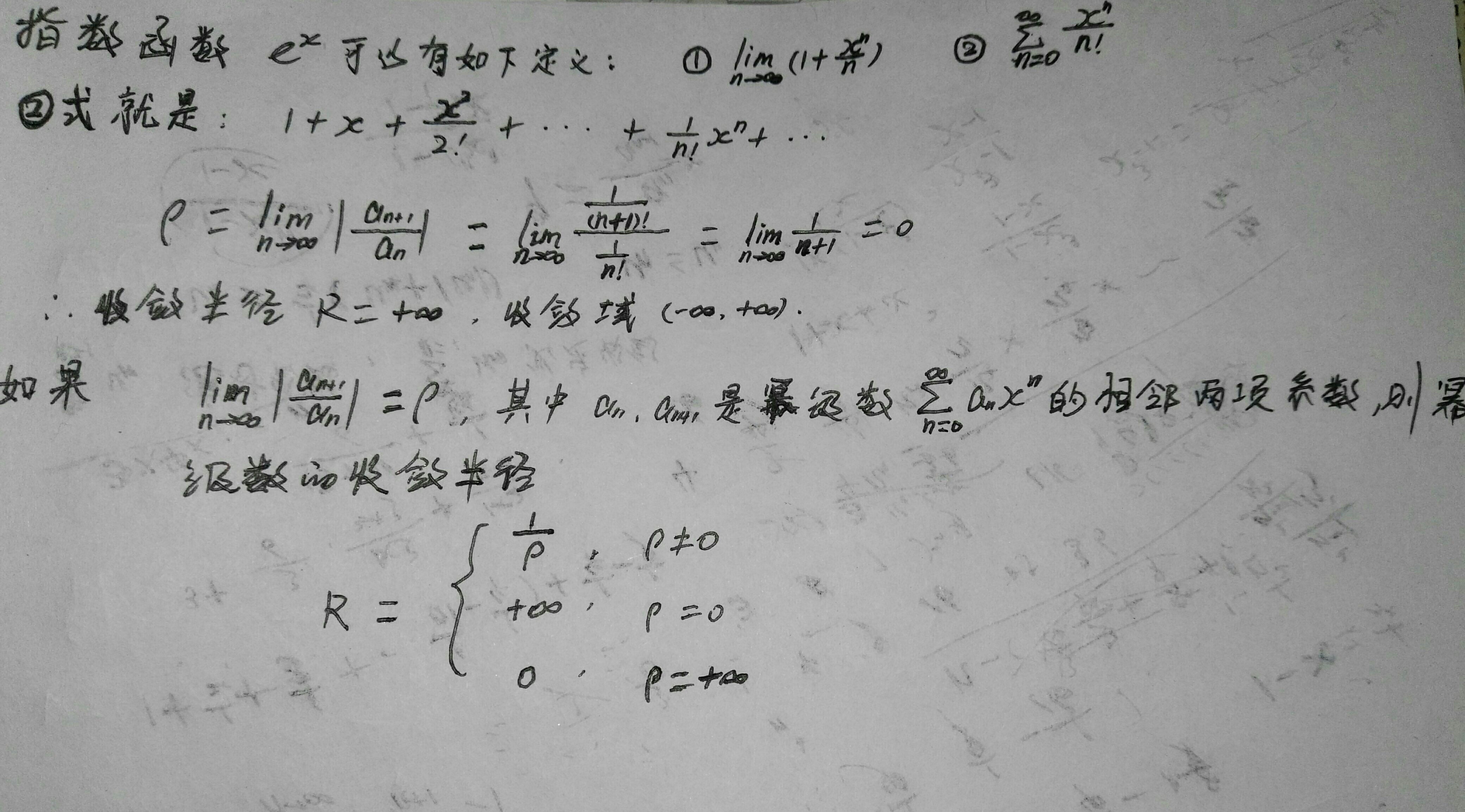
2.函数的幂级数展开

上图中的①式是函数幂级数的一般形式,如果幂级数收敛的话,必存在n阶导数,推导出级数的一般表达式。当x0不为0时,通常称为泰勒级数,当x0取0时,成为麦克劳林级数。对于指数函数的展开,通常按照麦克劳林级数展开,计算n阶导数,直到导数不存在时终止,然后计算x0=0时的导数值,接着把指数函数展开,最后判断收敛性。
函数的幂级数展开应用---欧拉公式
关于欧拉公式,是这么来的:
欧拉公式的证明还可以利用拉格朗日中值定理来求证,不做论述了。欧拉公式在物理中有很重要的应用,比如两束逆向的极光,磁场消失,电场增倍。后面的傅立叶变换将详细论述。
3.傅立叶级数
三角函数系:
三角函数系的基类似于矩阵的标准正交特征向量系。
傅立叶级数的系数求解:
傅立叶级数的收敛判定:
正弦级数和余弦级数
举个例子:
下面讨论一般周期函数的傅立叶级数
傅立叶级数的复数形式表达:
4.傅立叶变换
前面的3个部分从纯数学角度论述了傅立叶级数,如果不结合物理学的话,理解还是不到位的,不够形象。这部分将深入浅出重新解读前面的公式。首先呈现出连续傅立叶变换的公式,盯着看这个公式一会儿,你想到了什么?
这个公式的输入是函数,输出仍然是函数。由函数空间到函数空间的映射,立马想到是线性算子。如果是函数空间到实数域的映射,则是泛函数。这个公式把以时间为自变量的函数输入转变成以频率为自变量的函数,明显是一种空间的转换。于是想到了如下定义:
这是《实变函数与泛函数分析》中的经典线性算子。例5和傅立叶变换多么的相似。傅立叶变换本质上是函数空间到函数空间的变换,是一种线性算子。那么例4中的公式如何形象地理解呢?
傅立叶级数最形象的解释:
下面将对前面的公式进行通俗的解释:‘
傅立叶变换在信号学中是时域到频域的转换。从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。用另一种方法来观察世界的话,你会发现很多复杂的事物背后都有不变的东西,比如矩阵论中的基,这个静止的世界就叫做频域。再形象一点儿:
这是一段音频,一个随着时间变化的震动。它其实是由固定的音符叠加而成的,就是下面这个样子:
把上面的图简化一下:
图(1)
傅立叶变换就是把信号中的基分离出来,从时间转换到频率。
傅立叶级数的形象化解释:
前面的例子中有一个矩形波,这个矩形波是由很多频率,振幅不同的基本的正弦波叠加而成的,如下所示:
图(2)
当无穷多个正弦波叠加时,图像就会趋近于矩形。不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。还是上图的正弦波累加成矩形波,我们换一个角度来看看:
图(3)
这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。这里,不同频率的正弦波我们称为频率分量。
如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元,称之为“基波”。傅立叶级数分解后的公式里面第一个分量就是他。这里补充一下正弦波:


这个动图实际上反映了非复数形式的傅立叶级数分解,这些正弦波按照上面的形式叠加形成矩形波,他们是频域的基本组成单元。介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样了,图3从频率的方面看去:
对于傅立叶级数的一个最直接的用途。无论听广播还是看电视,我们一定对一个词不陌生——频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
先在纸上画一个sin(x),不一定标准,意思差不多就行。不是很难吧。
好,接下去画一个sin(3x)+sin(5x)的图形。
别说标准不标准了,曲线什么时候上升什么时候下降你都不一定画的对吧?
好,画不出来不要紧,我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。
但是在频域呢?则简单的很,无非就是几条竖线而已。
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
傅立叶变换
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。这句话比较绕嘴,实在看着费事可以干脆回忆第一章的图片。
而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个在频域非周期的连续信号。
傅立叶变换的复数形式解释:
关于复数和欧拉公式的意义,前面已经简单介绍过了。欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
前面非复数形式的变换,那个动图就已经很生动了,欧拉公式统一后是螺旋线的叠加,得到的是连续的频谱。


























