前面的两篇文章比较清楚浅显的介绍了线性回归、多项式回归,并了解到其实多项式回归也可以看作是一种特殊的线性回归形式,也就是说回归的核心就是线性回归。其原理都是最小二乘法,这是一种很简单、很方便的算法,但也有它的局限性,所以本文讲述另外的回归方式岭回归、LASSO回归,作为一个补充,解决最小二乘法的一些缺点。
最小二乘法的局限性:
上面是最小二乘法的核心算法,通过公式我们可以看到该公式成立的条件就是不等于0,也就是
能求逆(可以用linalg.det(X)等方法判断),而当变量之间的相关性较强(多重共线性),或者m(特征数)大于n(样本数),上式中的X不是满秩矩阵。那就会使得
的结果趋近于0,造成拟合参数的数值不稳定性增加(参数间的差距变化很大),这也就是普通最小二乘法的局限性。
下面通过希尔伯尔矩阵来验证最小二乘法的局限性(希尔伯特矩阵每列之间存在很强的相关性 ):
"""生成 10x10 的希尔伯特矩阵
"""
from scipy.linalg import hilbert
x = hilbert(10)
"""希尔伯特转置矩阵与原矩阵相乘
"""
import numpy as np
mat = np.linalg.det(np.matrix(x).T*np.matrix(x)) # det计算行列式 dot计算一维内积或多维矩阵相乘
print(mat) # x.T*x 趋近于0皮尔逊相关系数通常用于度量两个变量 X 和 Y 之间的线性相关程度,其值介于 -1 与 1 之间。其中,数值越趋近于 1 表示相关程度越高,反之趋近于 -1 则表示线性相关度越低。
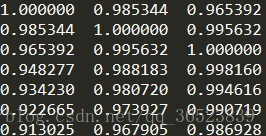
在pandas中提供了直接计算相关系数的方法 .corr(),我们再来验证一下列之间的相关性:
pd.DataFrame(x, columns=['x%d'%i for i in range(1,11)]).corr()可以看到,列之间的相关性是相当的大。
综上所示,普通最小二乘法带来的局限性,导致许多时候都不能直接使用其进行线性回归拟合,尤其是下面两种情况:
-
数据集的列(特征)数量 > 数据量(行数量),即 X 不是列满秩。
-
数据集列(特征)数据之间存在较强的线性相关性,即模型容易出现过拟合。
岭回归:
岭回归推导:
为了解决上述两种情况出现的问题,岭回归(Ridge Regression)应运而生。岭回归可以被看作为一种改良后的最小二乘法,它通过向损失中添加正则项(2-范数)有效防止模型出现过拟合,且有助于解决非满秩条件下求逆困难的问题,从而提升模型的解释能力。所以上面的损失函数变为:
转化为向量模式:
回归系数w的解析变为:
从上式中可以看到增加了一个 λ*(特征列大小)单位矩阵 引入惩罚项λ限制了所有w的和,减少不重要的参数项,统计学中也叫“缩减”。
这里仅简单的给出推导公式,没有更深入的解释,如果需要了解,可以查看官方一点的文档。
通过scilit-learn提供的方法可以很方便的使用岭回归。
岭回归拟合:
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)
-
alpha: 正则化强度,默认为 1.0,对应公式中的 λ。正则化强度; 必须是正浮点数。 正则化改善了问题的条件并减少了估计的方差。 较大的值指定较强的正则化。 Alpha对应于其他线性模型(如Logistic回归或LinearSVC)中的。 如果传递数组,则假定惩罚被特定于目标。 因此,它们必须在数量上对应。
-
fit_intercept: 默认为 True,计算截距项。如果设置为false,则不会在计算中使用截距(例如,数据预期已经居中)。 -
normalize: 默认为 False,不针对数据进行标准化处理。如果为真,则回归X将在回归之前被归一化。 当fit_intercept设置为False时,将忽略此参数。 当回归量归一化时,注意到这使得超参数学习更加鲁棒,并且几乎不依赖于样本的数量。 相同的属性对标准化数据无效。然而,如果你想标准化,请在调用normalize = False训练估计器之前,使用preprocessing.StandardScaler处理数据。 -
copy_X: 默认为 True,即使用数据的副本进行操作,防止影响原数据。 -
max_iter: 最大迭代次数,默认为 None。共轭梯度求解器的最大迭代次数。 对于'sparse_cg'和'lsqr'求解器,默认值由scipy.sparse.linalg确定。 对于'sag'求解器,默认值为1000。 -
tol: 数据解算精度。 -
solver: 根据数据类型自动选择求解器。{'auto','svd','cholesky','lsqr','sparse_cg','sag'} -
random_state: 随机数发生器。
更多的参数中文详解可以参考这里
比较重要的就是alpha参数的选择了,其代表了正则化强度,我们可以通过类似网格搜索的单层方式来得到不同的拟合结果(其中y值为随机创建的w乘上矩阵得到的):
w = np.random.randint(2,10,10) # 随机生成 w 系数
y_temp = np.matrix(x) * np.matrix(w).T # 计算 y 值
y = np.array(y_temp.T)[0] #将 y 值转换成 1 维行向量 相当于给矩阵创建一个真实值
"""不同 alpha 参数拟合
"""
alphas = np.linspace(-3,2,20)
coefs = []
for a in alphas:
ridge = Ridge(alpha=a, fit_intercept=False)
ridge.fit(x, y)
coefs.append(ridge.coef_)
"""绘制不同 alpha 参数结果
"""
from matplotlib import pyplot as plt
plt.plot(alphas, coefs) # 绘制不同 alpha 参数下的 w 拟合值 这里一共10条
plt.scatter(np.linspace(0,0,10), parameters[0]) # 普通最小二乘法拟合的 w 值放入图中
plt.xlabel('alpha')
plt.ylabel('w')
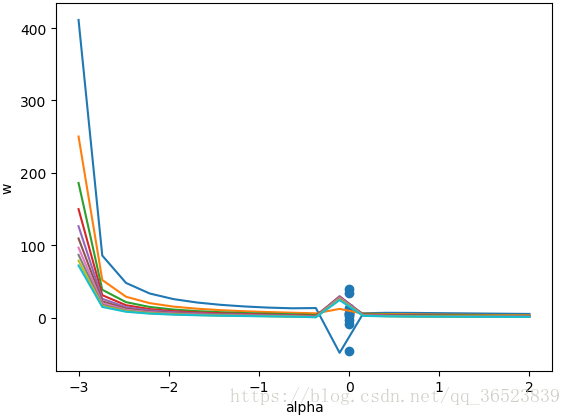
plt.title('Ridge Regression')
plt.show()由图可见,当 alpha 取值越大时,正则项主导收敛过程,各 w 系数趋近于 0。当 alpha 很小时,各 w 系数波动幅度变大。 所以可以选择收敛基本平稳的alpha点。
LASSO回归:
当我们使用普通最小二乘法进行回归拟合时,如果特征变量间的相关性较强,则可能会导致某些 w 系数很大,而另一些系数变成很小的负数。所以,我们通过上文中的岭回归添加 L2 正则项来解决这个问题。
与岭回归相似的是,LASSO 回归同样是通过添加正则项来改进普通最小二乘法,不过这里添加的是 L1 正则项。即:
这里关于L1、L2没有做很详细的解释,如果需要可以参考这里,简单说下:
L1:L1正则化最大的特点是能稀疏矩阵,进行庞大特征数量下的特征选择
L2:L2正则能够有效的防止模型过拟合,解决非满秩下求逆困难的问题
LASSO回归拟合:
sklearn.linear_model.Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')
-
alpha: 正则化强度,默认为 1.0。 -
fit_intercept: 默认为 True,计算截距项。 -
normalize: 默认为 False,不针对数据进行标准化处理。 -
precompute: 是否使用预先计算的 Gram 矩阵来加速计算。 -
copy_X: 默认为 True,即使用数据的副本进行操作,防止影响原数据。 -
max_iter: 最大迭代次数,默认为 1000。 -
tol: 数据解算精度。 -
warm_start: 重用先前调用的解决方案以适合初始化。 -
positive: 强制系数为正值。 -
random_state: 随机数发生器。 -
selection: 每次迭代都会更新一个随机系数。
"""使用LASSO 回归拟合并绘图
"""
from sklearn.linear_model import Lasso
alphas = np.linspace(-2,2,10)
lasso_coefs = []
for a in alphas:
lasso = Lasso(alpha=a,fit_intercept=False)
lasso.fit(x,y)
lasso_coefs.append(lasso.coef_)
plt.plot(alphas,lasso_coefs) # 绘制不同alpha下的 w 拟合值
plt.scatter(np.linspace(0,0,10),parameters[0]) # 普通最小二乘法的 w 放入图中
plt.xlabel('alpha')
plt.ylabel('w')
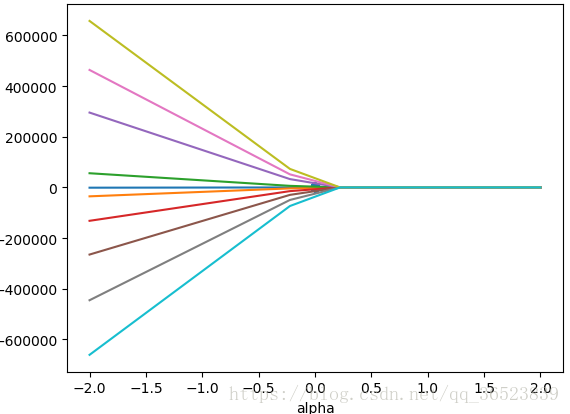
plt.title('Lasso Regression')
plt.show()由图可见,当 alpha 取值越大时,正则项主导收敛过程,各 w 系数趋近于 0。当 alpha 很小时,各 w 系数波动幅度变大。
参考文章:
实验楼