PCA(Principal Components Analysis)

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/u012071811/article/details/86225132

一、定义符号

主成分分析（Principal Components Analysis, PCA）是一种降维方法。为了更好的解释该算法，首先假设数据集为 $\{x^{(i)}; i=1,2, \dots, m\}$，其中 $x^{(i)} \in \mathbb {R}^n$，也就是说数据集一共包含 m 条数据，每条数据的特征向量的维度为 n。

二、中心化和标准化

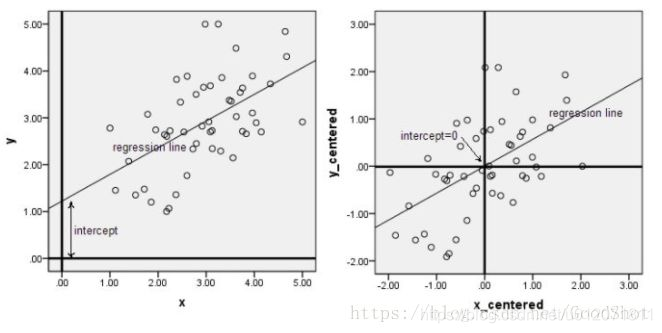
中心化又叫零均值化，中心化（零均值化）后的数据均值为零。下面两幅图是数据做中心化前后的对比，可以看到其实就是一个平移的过程，平移后所有数据的中心是(0, 0)。

数据标准化的目的就是使各个特征都在同一尺度下被衡量。

三、Z-score 标准化

Z-score 标准化（也叫 0-1 标准化），这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为 0，标准差为 1。Z-score 标准化的公式如下：

$x^{*} = \frac{x - \mu}{\sigma}$

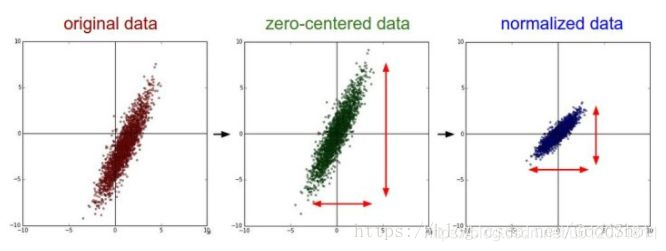
我们可以发现 Z-score 标准化的过程中是包含中心化的。以下图片展示了一组数据进行 Z-score 标准化的过程。左图表示的是原始数据，中间的是中心化后的数据，右图是将中心化后的数据除以标准差，得到的标准化后的数据，可以看出每个维度上的尺度是一致的（红色线段的长度表示尺度）。

想要使用 PCA 算法，需要先对数据做以下处理：

1. $\mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$
2. $x^{(i)} = x^{(i)} - \mu$
3. $\sigma_j^2 = \frac{1}{m} \sum_i(x_j^{(i)})^2$
4. $x_j^{(i)} = \frac{x_j^{(i)}}{\sigma_j}$

整个过程其实就是 Z-score 标准化的过程。

四、PCA 算法的基本思想

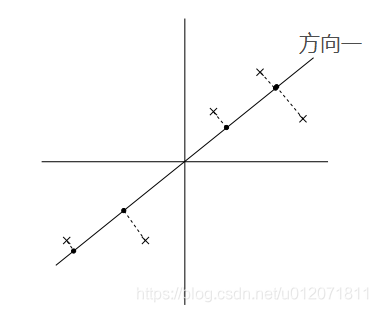
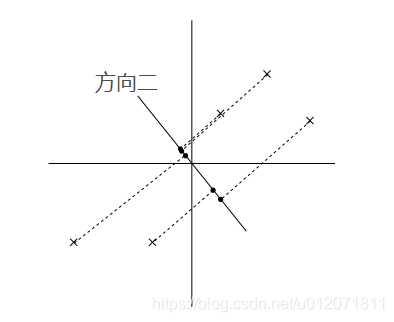
PCA 算法的基本思想就是寻找到数据的主轴方向，我们希望数据在主轴方向上能够被更好的区分开，直观的说就是我们希望数据在主轴上尽量分散，更具体的就是指所有的点在主轴方向的投影点的方差最大。比如在以下两个图中，在方向一上，数据更分散，投影点的方差最大，所以如果从这两个方向上选一个主轴的话，应该选方向一。

在数据已经做了 Z-score 标准化的前提下，数据的均值为 0，其投影点的均值也为 0。

$max \frac{1}{m} \sum_{i=1}^{m}(x^{(i)^T}u - 0)^2 \\ \Rightarrow max \frac{1}{m} \sum_{i=1}^{m} \mu^T x^{(i)} x^{(i)^T} \mu \\ \Rightarrow max \mu^T \Big( \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)^T} \Big) \mu \\$

(1) 上述第一个式子里的 $x^{(i)^T} \mu$ 就是 $x^{(i)}$ 这个向量在投影方向 $\mu$ 上的长度。这里的 $\mu$ 是单位向量，即 $\lVert \mu \rVert = 1$。
(2) 上述第二个式子是把向量内积的平方换了一个写法。
(3) 上述第三个式子又对式子做了一个变形，不难看出 $ \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)T} $ 是一个矩阵，并且这个矩阵是对称矩阵（实际上是一个协方差矩阵）。
(4) 纵观整个式子，最终的目标则是找到使整个式子取到最大值的向量 $\mu$ ，所以这是一个最优化问题。

五、求解 μ 与降维

$\mu$ 是一个单位向量，这其实是这个最优化问题的约束条件（ $\lVert \mu \rVert = 1$），可以使用拉格朗日方程来求解该最优化问题：
$\begin{aligned} l =& \mu^T \Big( \frac{1}{m} \sum_{i=1}^m x^{(i)} x^{(i)^T} \Big) \mu - \lambda (\lVert \mu \rVert - 1)\\ =& \mu^T \Sigma \mu - \lambda(\mu^T \mu - 1) \end{aligned}$
对 $\mu$ 求导：
$\begin{aligned} \triangledown_{\mu} l =& \triangledown_{\mu} \mu^T \Sigma \mu - \lambda \triangledown_{\mu} \mu^T \mu \\ =& \Sigma \mu - \lambda \mu \end{aligned}$
令导数为 0，可以发现 $\mu$ 是 $\Sigma$ 的特征向量。再因为矩阵 $\Sigma$ 是对称矩阵，所以一定能找到 n 个相互正交的特征向量，如果要选出 k 个主轴方向，我们从 n 个特征向量里选出 k 个最大的特征值对应的特征向量即可。假设选出的 k 个特征向量为：

$\{\mu_1, \mu_2, \dots, \mu_k\}$

则可以通过以下公式将原来是 n 维的 $x^{(i)}$ 降为 k 维的 $y^{(i)}$：

$[y_1^{(i)}, y_2^{(i)}, \dots, y_k^{(i)}] = [u_1^T x^{(i)}, u_2^T x^{(i)}, \dots, u_k^T x^{(i)}]$

六、参考

• 斯坦福机器学习公开课 —— 吴恩达
• 斯坦福ML机器学习公开课笔记 —— 张雨石
• 中心化（又叫零均值化）和标准化（又叫归一化）
• 个人博客主页，欢迎来访^_^
• 个人公众号，欢迎来访^_^