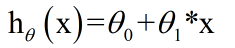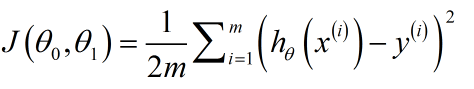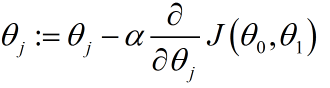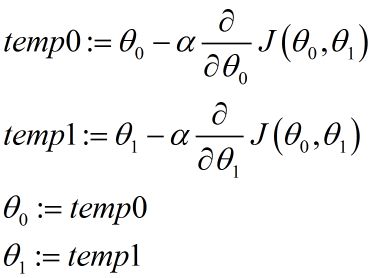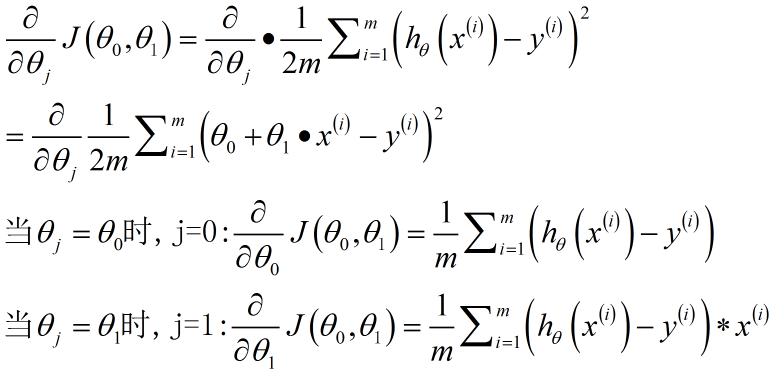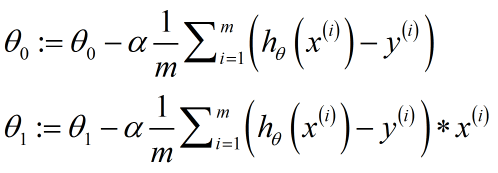第二章 单变量线性回归
模型描述
房价预测的例子:
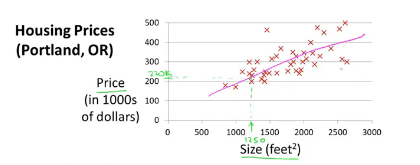
这是一个房价预测的例子,同时也是一个一元线性回归问题(单变量线性回归)。
房价预测之所以是监督学习的例子是因为每一个样本都有一个正确的答案。
正式的定义:在监督学习里,设有一个数据集,这被称为一个训练集。
符号定义:
m表示训练样本的数量,
x表示输入变量(或者特征),
y表示输出变量(预测的目标变量),
(x,y)表示一个训练样本,
(x^(i),y^(i))表示第i个训练样本(i指的是索引,表示第i个训练样本)。
监督学习算法的工作流程: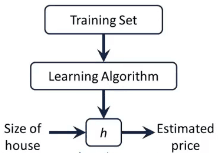
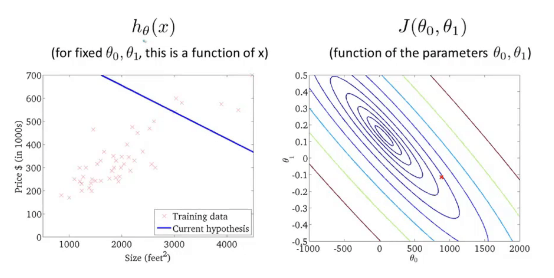
在房价预测的例子中,提供一个训练集,学习算法的任务是输出一个函数,通常用h表示。
h表示假设函数,作用是把房子的大小作为输入变量,房子的价格作为输出变量,h是一个引导从x得到y的函数。
对于假设h我们可以用一条直线描述,用线性函数预测房价值:
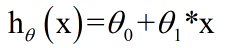
代价函数
对上述的公式来说,我们要做的是如何选择θ0和θ1,选择不同的参数将得到不同的假设和假设函数。
表示关于θ0和θ1的最小化过程,这意味着我们要找到θ0和θ1的值来使这个表达式的值最小,即把问题变成:找到能使训练集中预测值和真实值的差的平方的和的1/2m最小的θ0和θ1的值,这将是线性回归的整体目标函数。
定义代价函数:
通过对求J(θ0,θ1)最小值来满足需求。
这就是代价函数,也被称为平方误差函数,有时称为平方误差代价函数,平方误差代价函数是解决回归问题最常用的手段。
代价函数的例子:
(1)将θ0设为0,此时学习算法的优化目标是通过θ1选择获得最小的J(θ1),minimizeJ(θ1)就是线性回归的目标函数,最小化J(θ1)来找到一条最符合数据的直线。
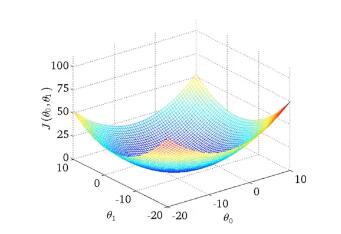
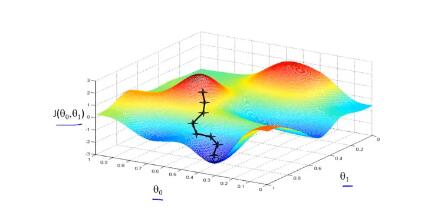
(2)将θ0和θ1都考虑进来,得到一个3D曲面图如下:
横轴为θ0和θ1,若改变参数的值,会得到不同的J(θ0,θ1)。竖轴为曲面的高度,就是J(θ0,θ1)的值。这个类似 碗的形状就是代价函数的形状。使用等高线图或称为等高图像展示这些曲面,通过这些图像,更好地理解代价函数J的意义, 如何对应不同的假设函数以及接近代价函数J最小值的点,对应着更好的假设函数,同样,我们真正想要的是一个高效的算法 自动寻找代价函数J的最小值对应的θ0和θ1。
等高线图
梯度下降
梯度下降是一种可以将代价函数J最小化的算法,它不仅被用在线性回归上,还被广泛应用于机器学习的众多领域。
问题概述:
有一个函数,想要用一个算法求最小化函数J(min(J(θ0,θ1)))
梯度下降思路(outline):
(1)给定θ0和θ1的初始值,通常将他们初始设为0。
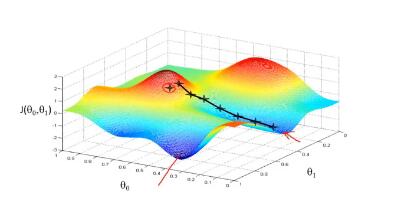
(2)不停地一点点改变θ0和θ1来使J(θ0,θ1)变小,直到找到J的最小值或局部最小值。梯度下降的过程如下图:
就像下山一样,每次在一点环顾四周,往最陡峭的路向下走,用图形的方式更形象的表示。但如果你的起始点偏移了一些,会得到完全不同的局部最优解,就像上面图像所示,这就是梯度下降算法的一个特点。
梯度下降算法的数学定义如下:
反复做上述这一步,直至收敛。
符号定义如下:
:=这个符号表示赋值运算符;α被称为学习速率,用来控制梯度下降时,即下山时该迈出多大的步子。
正确实现梯度下降的方法,即同步更新,如下所示:
这样就能够同步更新θ0和θ1,这是正确的实现方法。
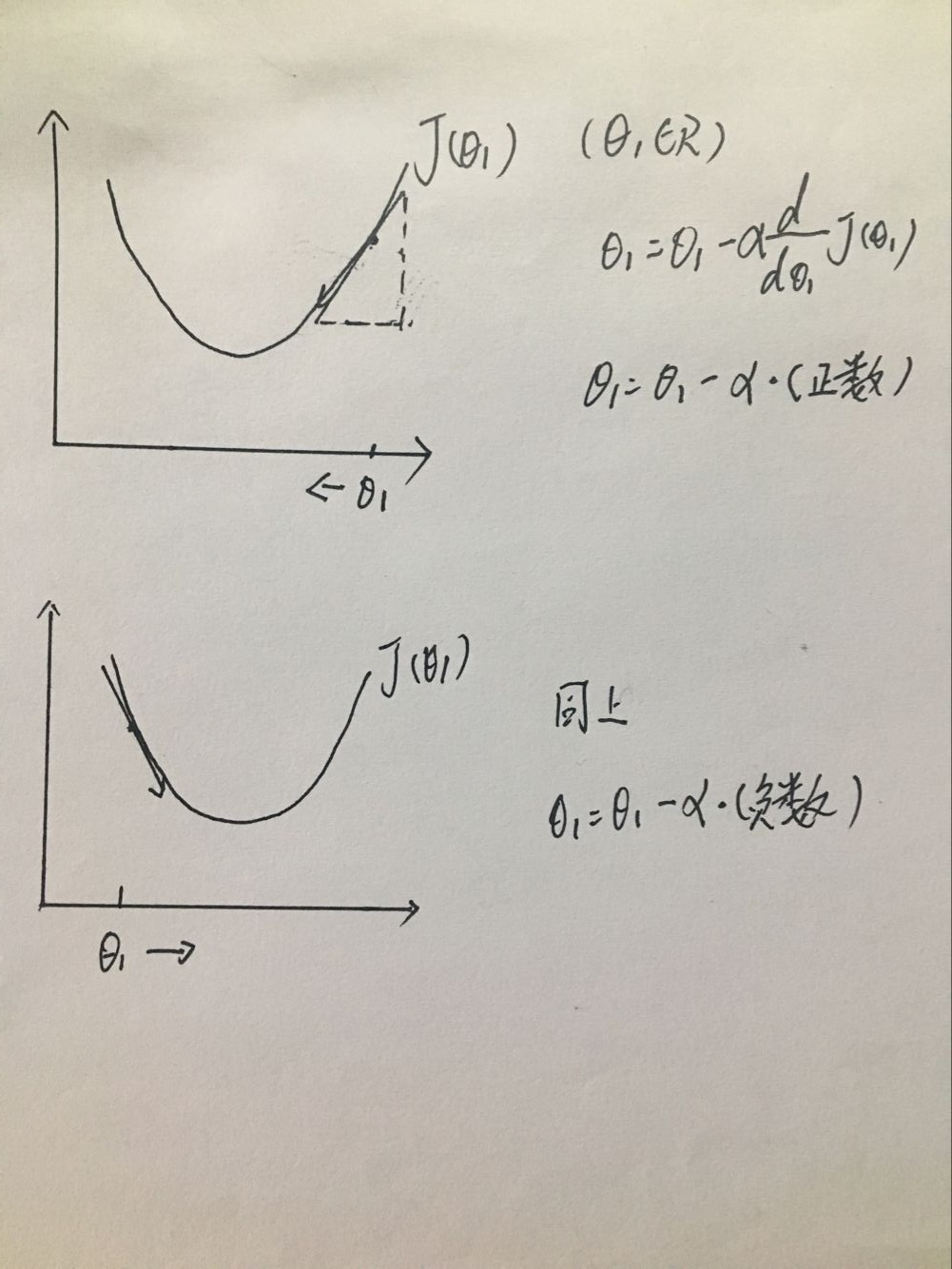
梯度下降的运动方式:
首先,用简单化的例子来讲述,设θ0=0,此时可以画出的图像,如下:
从图中可以看出:第一个坐标系中,此时的方向是开始减小,往使最小的局部最低点走;第二个坐标系中,此时的方向是 开始减小,同样也是往使最小的局部最低点走。
根据是学习速率,有以下结论:
1.如果α(学习速率)太小,则梯度下降法会收敛的很慢;
2.如果α太大,则梯度下降法每次下降很快,可能会越过最小值,最终会导致无法收敛甚至发散。
3.如果已经在局部最优点,θ1将不再改变,那么梯度下降法更新其实什么都没做,意味着它始终保持在局部最优值。
在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的幅度,这是因为接近局部最低点时,导数 值 自动变得越来越小,这就是梯度下降的运动方式,可以用梯度下降算法来尝试最小化任何代价函数J。
线性回归的梯度下降:
这一节中要将梯度下降和代价函数结合得到线性回归算法,它可以用直线模型来拟合数据。
这是梯度下降法和和线性回归模型(包括了假设函数和平方差代价函数)。
我们要做的是将梯度下降应用到最小化平方差代价函数,关键步骤是导数项。
探讨梯度下降算法的导数项:将上面的结果应用到梯度下降算法中,就得到了回归的梯度下降算法:
有时我们把这个算法也称为Batch梯度下降算法,每一步下降都遍历了整个训练集的样本。
这就是我们的第一个机器学习算法--线性回归算法。