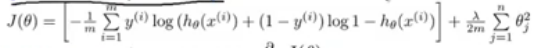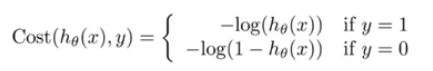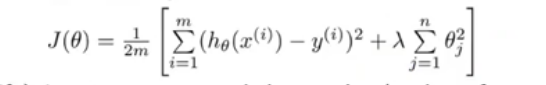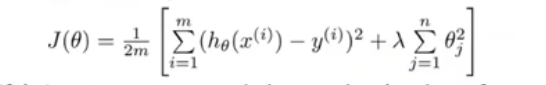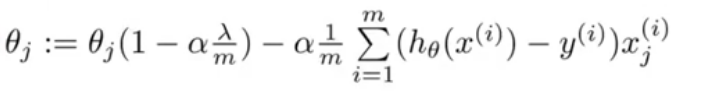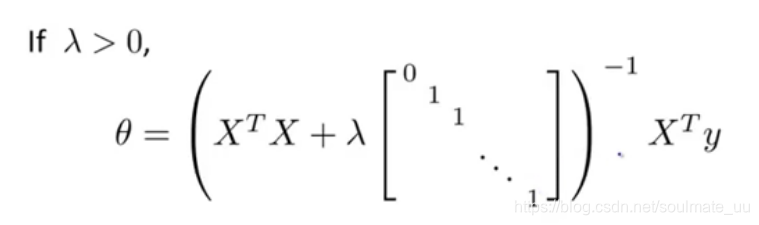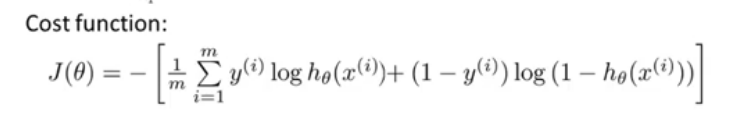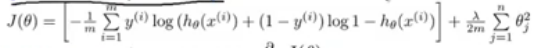上一篇笔记主要讨论预测一个取值连续的值,本章讨论取值离散的情况。
————————————————————————————————————————
————————————————————————————————————————
1. Logistic回归
1.1 简单的二分类问题
当使用前面介绍的线性回归算法时,不太适用。因此引入一个分类算法,即Logiistic回归。
- 假设方程:
hθ(x)=g(θTx),其中
g(z)=1+e−z1,
g(z)被称为Sigmoid函数或者Logistic函数。
其函数图像如:
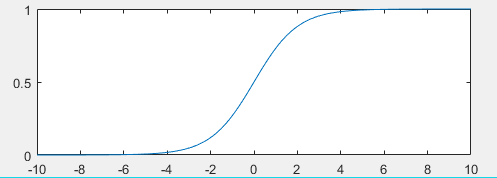
因此,
hθ(x)=1+e−θTx1,
hθ(x)的值必然介于(0,1)之间。
hθ(x)代表什么呢?
hθ(x)表示当输入
x时,
y=1的概率。有时也写成:
hθ(x)=p(y=1∣x;θ)。
eg.在判断良性/恶性肿瘤时,输入某个
x,得到输出为0.7,即表示有70%的可能是恶性。
-
决策界限:根据Logistic函数图像的性质,当
θTx>0时,
hθ(x)>0.5,此时可预测
y=1;当
θTx<0时,
hθ(x)<0.5,此时可预测
y=0。
决策边界就是满足
θTx=0时的边界。
决策边界不是训练集的属性,而是假设函数的一个属性。
也就是说只要给定了参数向量
θ,决策边界也就确定了。并 不是用训练集来定义的决策边界,我们用训练集来拟合参数
θ。
对于非线性的决策边界,可以利用多项式回归。同样其边界也是使得
θTxi=0的边界线。
-
代价函数: 不可再用平方代价函数,因为此时的
J(θ)不是一个凸函数,无法利用梯度下降算法计算全局最小值 。
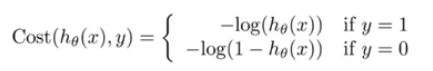
当
y=1时,代价函数图像如下:
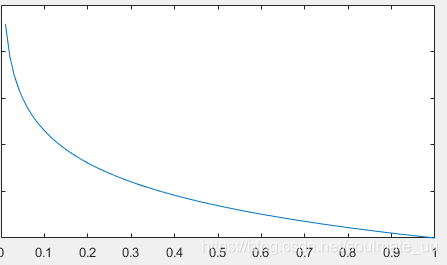
即若
hθ(x)趋于1,则代价函数的值趋于0;若
hθ(x)趋于0,则代价函数的值趋于无限大。
当
y=0时,代价函数图像如下:
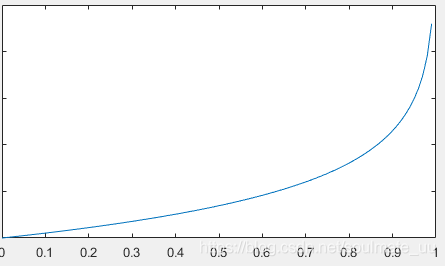
即若
hθ(x)趋于0,则代价函数的值趋于0;若
hθ(x)趋于1,则代价函数的值趋于无限大。
- 简化代价函数与梯度下降

其中,
Cost(hθ(x),y)又可以写作:
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
J(θ)也可以写做:
J(θ)=m1i=1∑m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
J(θ)是凸函数。
梯度下降算法和之前的一样:

简化后,可以得到与线性回归相似的计算式,只不过此时的
hθ(x)变了。

扫描二维码关注公众号,回复:
7195832 查看本文章

- 高级优化算法
除梯度下降算法之外,有3种更加复杂的高级优化算法:共轭梯度法、BFGS、L-BFGS
优点:1、无需手动选择学习率
α 2、收敛速度快
缺点:相当复杂,所以直接调用软件库会更加方便,不同的库实现这些算法也是有区别的。
1.2 多分类问题
例如:天气分类问题:sunny\cloudy\rain\snow(y取不同的离散值,如y=1\y=2\y=3\y=4)
二分类和多分类:
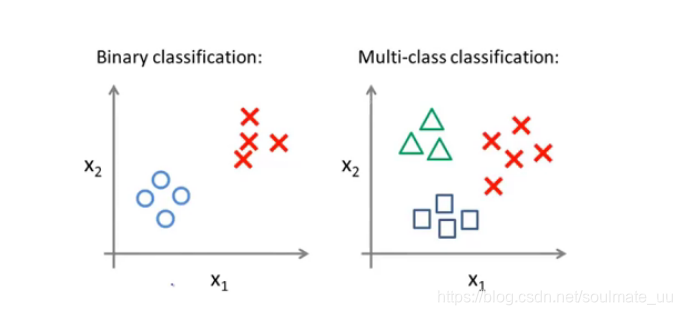
相比前面的二分类问题,因为
p(y=1∣x;θ)+p(y=0∣x;θ)=1,所以只需要求一个
hθ(x)=p(y=1∣x;θ),那么另一个也知道了,即可根据
hθ(x)的值进行分类。
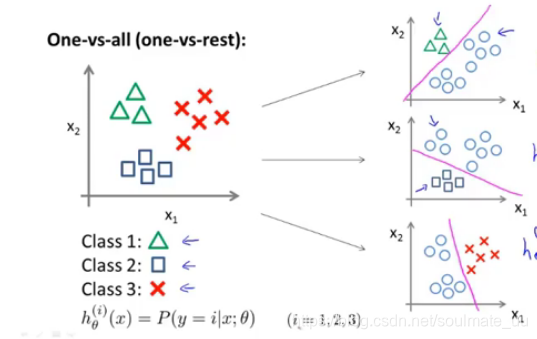
在多分类问题中,如下图:要计算
hθ(i)(x)=p(y=i∣x;θ),(i=1,2,3)
对于一个输入值,比较
hθ(i)(x)的大小,取其最大值对应的
i,即划分为
y=i。
2. 正则化
2.1 过拟合问题
- 线性回归中的:欠拟合(高偏差)、合适的拟合、过拟合(高方差)
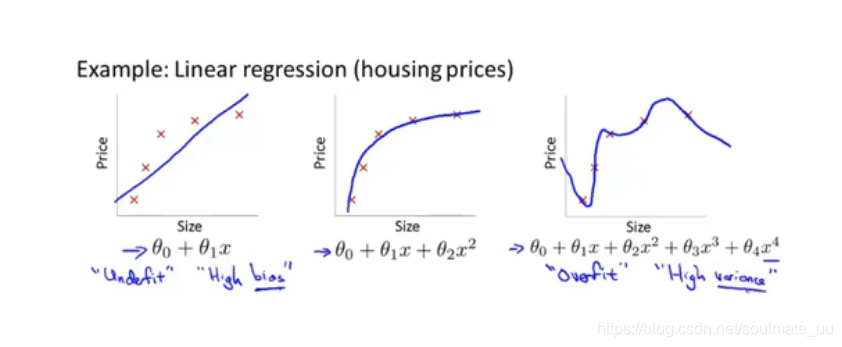
- 逻辑回归中的:欠拟合、合适的拟合、过拟合
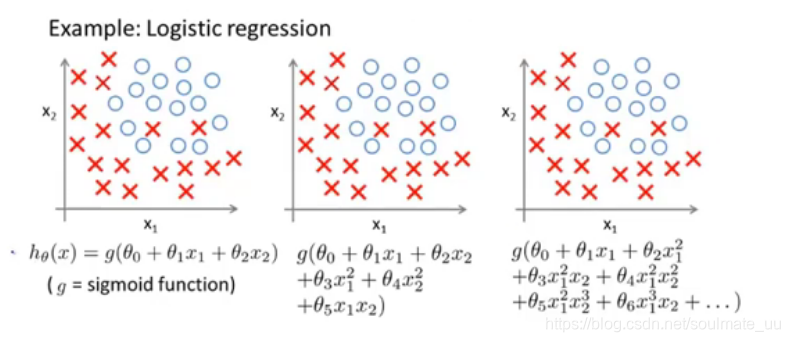
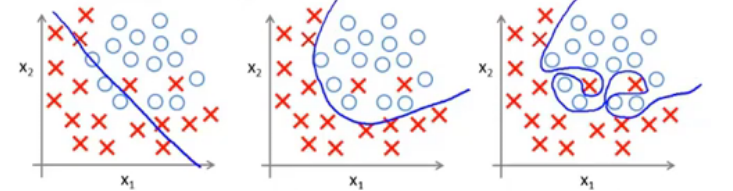
过拟合:假设函数能够拟合几乎所有的数据,这就面临着函数太过庞大、变量过多的问题,没有足够的数据来约束它,以获得一个好的假设函数。千方百计地拟合训练集的数据,容易导致它无法泛化到新的样本中,无法进行预测。
- 解决过拟合问题的方法:
1.减少变量的数目:a.手动检查变量清单 b.利用模型选择的算法
2.正则化:保留所有的变量,但是减少量级或者参数
θ的大小。
2.2 代价函数与正则化
正则化过程:在代价函数基础上加入正则项:
λj=1∑nθj2,其中,
λ是正则化参数。
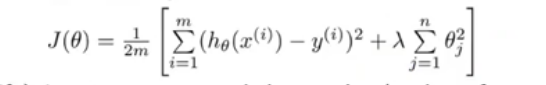
在正则化参数的影响下,为了使代价函数取最小值,就会尽量减小某些参数
θj的值,特别是使某些参数趋于 0,此时就相当于减少了变量数目,简化了假设函数,使拟合曲线更加平滑,而非拟合所有训练数据。
当然,若
λ过大,会使所有的参数趋于0,此时就是一条直线拟合,变成了欠拟合的问题。
例如:
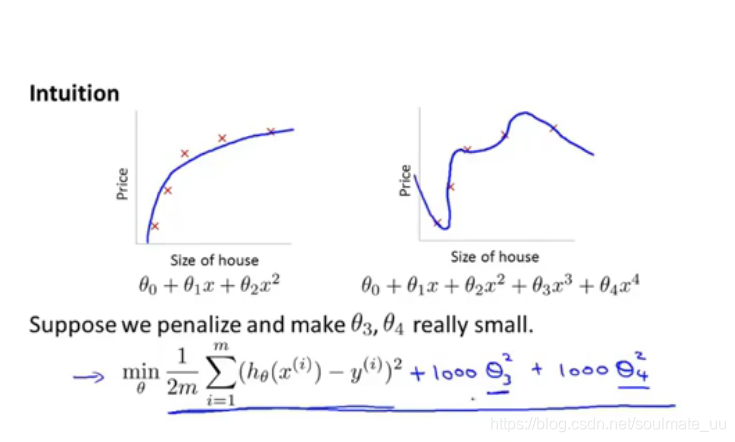
为了求代价函数的最小值,我们会使
θ3、θ4为0,变量少了,此时第二幅图过拟合就变成第一幅图的拟合了。
2.3 线性回归的正则化
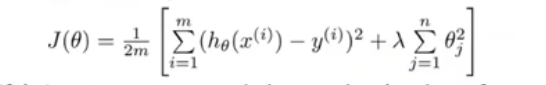
应用梯度下降算法,对上式求偏导,可得:
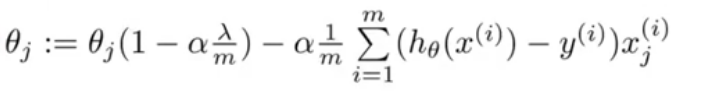
其中,
1−αmλ是一项比1略小的数,如0.99。所以
θj在每次更新后,都会缩小一点,往0的方向更加靠近。
利用矩阵的知识,在学习笔记(一)的基础上,可以得到: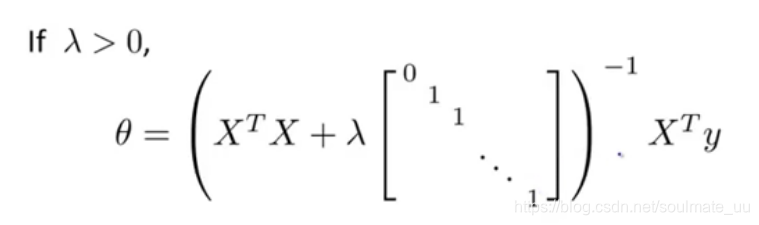
λ 后面的矩阵是(n+1)X(n+1)维的。
2.4 Logistic回归的正则化
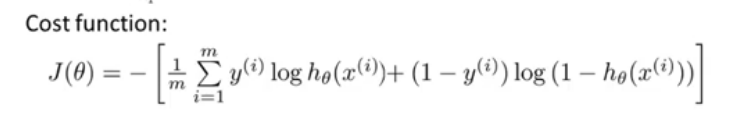
加入正则项: