第八章正则化
过拟合问题
这一节中将讲述什么是过度拟合问题。
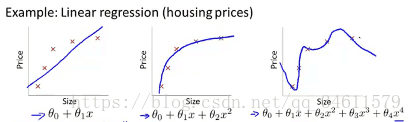
在数据拟合中,看一看下面的三种情况:
第一种称之为欠拟合,也叫高偏差;
第二种刚好拟合了数据;
第三种称之为过拟合,也叫高方差。在过拟合中,假设函数很好的匹配了训练集,但并不能很好的匹配测试集。
概括的说,过度拟合问题将会在变量过多的时候出现,它不能很好地泛化在新的样本中。上述的图片展示的是线性回归中的过度拟合现象,类似的同样可以应用到逻辑回归中,可以看一下下面的三种情况:
面对过拟合问题,我们有两种解决方式:
(1)尽量减少选取变量的数量,
方法:可以通过人工检查变量清单选择应该保留的变量;
可以使用模型算法自动的选择应该保留的变量。
(2)正则化,在保留所有特征量的情况下,但需要减少量级或减小θj。
当有很多特征时,其中每个变量都能对预测的y值产生一点影响。
代价函数
这一节中主要介绍正则化是怎样运行的。
在上一节中,可以看到通过二项式去拟合数据可以达到不错的效果,而用阶数过高的多项式去拟合数据会得到比较扭曲的线,虽然更好的拟合了数据,但出现了过拟合问题。
正则化的思想:如果参数值较小,参数值较小意味着会得到一个更简单的假设模型,这样也就更不让容易出现过拟合的问题。
利用正则化的思想下,我们应修改我们的代价函数如下:
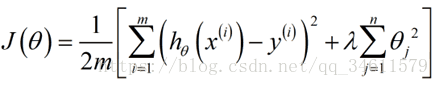
修改代价函数中,这里的λ被称为正则化参数。这个正则化参数的作用就是控制两个不同目标的取舍,
第一个目标更好地去拟合训练集的目标,第二个目标是将参数控制得更小。λ的作用就是控制这两个目标之间的平衡关系。
如果λ 的取值过小,则抑制的效果越弱,而λ的取值过大,则会导致欠拟合现象。对于线性回归,推导了基于梯度下降和正规方程两种算法,这一节中主要介绍这两种算法推广到正则化的线性回归中去。
修改之后的梯度下降法:
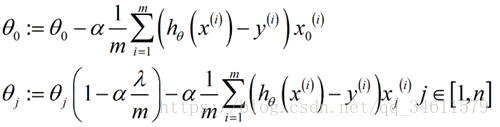
修改之后的正规方程法:

增加的矩阵是个n+1维的方阵,对角线上除了第一个元素为0其他都为1。
逻辑回归的正则化
这一节中主要介绍这两种算法推广到正则化的逻辑回归中去。
修改后的逻辑回归中的代价函数:
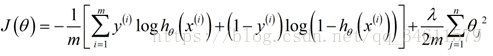
修改之后的梯度下降法: