线性最小二乘法拟合实验及代码详解

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/xiaohen123456/article/details/80311982

1. 实验目的

了解法方法求解步骤以及QR分解方法具体实现方式，通过最小二乘法得出最佳的拟合系数；

2. 实验内容

求一个二次多项式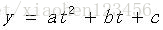，使得在最小二乘意义下拟合下面的数据

t	-1	-0.75	-0.5	0	0.25	0.5	0.75
y	1.00	0.8125	0.75	1.00	1.3125	1.75	2.3125

3. 实验步骤

1、最小二乘法的拟合曲线（即,估计值,含有未知数）
2、真实值减去估计值,然后平方.
3、对未知数求导,令其等于0,这样使得误差最小.
4、根据方程组,求解未知数.

4. 结果与分析

结果为：

x =

 

    1.0000

    1.0000

    1.0000

 

b =

    1.0000

    1.0000

1.0000

 

5. 实验总结

通过上面的实验我们发现法方法求解步骤以及QR分解方法都能够较好的拟合原始数据。

附录

Household变换：

function [v,beta]=house(x)

if nargin<1 x=rand(10,1); end

n=length(x); v=zeros(n,1);

% eta=max(abs(x));

eta=norm(x,inf);

x=x/eta;

deta=sum(x(2:n).^2);

v(2:n)=x(2:n);

if deta==0

    beta=0;

else

    alpha=sqrt(x(1)^2+deta);

    if x(1)<=0

        v(1)=x(1)-alpha;

    else

        v(1)=-deta/(x(1)+alpha);

    end

    beta=2*v(1)^2/(deta+v(1)^2);

    v=v/v(1);

end

 

H=eye(n)-beta*v*v';

QR分解：

function [A,d,b]=QR(A,b)

[m,n]=size(A); d=zeros(n,1);

for j=1:n

    if j<m

        [v,beta]=house(A(j:m,j));

        A(j:m,j:n)=(eye(m-j+1)-beta*v*v')*A(j:m,j:n);

        b(j:m)=(eye(m-j+1)-beta*v*v')*b(j:m);

        d(j)=beta;

        A(j+1:m,j)=v(2:m-j+1);

    end

end

clc

clear all

y=[1.00 0.8125 0.75 1.00 1.3125 1.75 2.3125]';

n=length(y);

A=ones(n,1);

t=[-1 -0.75 -0.5 0 0.25 0.5 0.75]';

plot(t,y,'r.','markersize',20)

A=[A t t.^2];

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%法方程求解最小二乘问题

x=A'*A\A'*y

t0=-1:0.05:0.75;

y0=x(1)+x(2)*t0+x(3)*t0.^2;

hold on 

plot(t0,y0,'-b')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%QR方法解最小二乘问题

[A,d,b]=QR(A,y);

m=size(A,2); b=b(1:m);

for j=m:-1:2

    b(j)=b(j)/A(j,j);

    b(1:j-1)=b(1:j-1)-b(j)*A(1:j-1,j);

end

b(1)=b(1)/A(1,1);

b

y1=b(1)+b(2)*t0+b(3)*t0.^2;

hold on 

plot(t0,y1,'-g')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

title('最小二乘问题')

legend('原始数据','法方程法拟合数据','QR方法拟合数据')

hold off