多目标优化算法（一）NSGA-Ⅱ

0. 前言

这个算法是本人接触科研学习实现的第一个算法，因此想在这里和大家分享一下心得。

1. 算法简介

NSGA-Ⅱ算法，即带有精英保留策略的快速非支配多目标优化算法，是一种基于Pareto最优解的多目标优化算法。

1.1 Pareto支配关系以及Pareto等级

Pareto支配关系：对于最小化多目标优化问题，对于n个目标分量 $f_i(x), i=1...n$ ，任意给定两个决策变量 $X_a$ ， $X_b$ ,如果有以下两个条件成立，则称 $X_a$ 支配 $X_b$ 。
1.对于 $\forall i \in {1,2,...,n}$ ，都有 $f_i(X_a) \leq f_i(X_b)$ 成立。
2. $\exists i \in {1,2,...,n}$ ，使得 $f_i(X_a) <f_i(X_b)$ 成立。
如果对于一个决策变量，不存在其他决策变量能够支配他，那么就称该决策变量为非支配解。
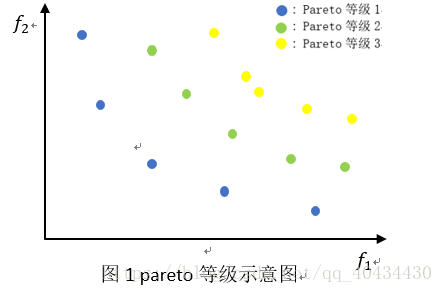
Pareto等级：在一组解中，非支配解Pareto等级定义为1，将非支配解从解的集合中删除，剩下解的Pareto等级定义为2，依次类推，可以得到该解集合中所有解的Pareto等级。示意图如图1所示。
在这里插入图片描述

1.2 快速非支配排序

假设种群大小为P，该算法需要计算每个个体p的被支配个数 $n_p$ 和该个体支配的解的集合 $S_p$ 这两个参数。遍历整个种群，该参数的计算复杂度为 $O(mN^2)$ 。该算法的伪代码如下：
1.计算出种群中每个个体的两个参数 $n_p$ 和 $S_p$ 。
2.将种群中参数 $n_p=0$ 的个体放入集合 $F_1$ 中。
3.for 个体 $i \in F_1$ :
        for 个体 $l \in S_i$ ：
                $n_l=n_l-1$ ；(该步骤即消除Pareto等级1对其余个体的支配，相当于将Pareto等级1的个体从集合中删除)
                if $n_l=0$ ：
                       将个体l加入集合 $F_2$ 中。
                end
        end
end
4.上面得到Pareto等级2的个体的集合 $F_2$ ，对集合 $F_2$ 中的个体继续重复步骤3，依次类推直到种群等级被全部划分。

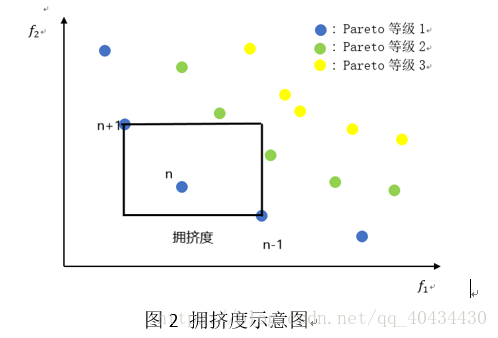
1.3 拥挤度

为了使得到的解在目标空间中更加均匀，这里引入了拥挤度 $n_d$ ，其算法如下：

令参数 $n_d=0，n∈1…N$ 。
for 每个目标函数 $f_m$ ：
        ① 根据该目标函数对该等级的个体进行排序，记 $f_m^{max}$ 为个体目标函数值 $f_m$ 的最大值， $f_m^{min}$ 为个体目标函数值 $f_m$ 的最小值；
        ② 对于排序后两个边界的拥挤度 $1_d$ 和 $N_d$ 置为∞；
        ③ 计算 $n_d=n_d+(f_m (i+1)-f_m (i-1))/(f_m^{max}-f_m^{min})$ ,其中 $f_m (i+1)$ 是该个体排序后后一位的目标函数值。

end

从二目标优化问题来看，就像是该个体在目标空间所能生成的最大的矩形（该矩形不能触碰目标空间其他的点）的边长之和。拥挤度示意图如图2所示。

1.4 精英保留策略

1.首先将父代种群 $C_i$ 和子代种群 $D_i$ 合成种群 $R_i$ 。
2.根据以下规则从种群 $R_i$ 生成新的父代种群 $C_{i+1}$ ：
①根据Pareto等级从低到高的顺序，将整层种群放入父代种群 $C_{i+1}$ ，直到某一层该层个体不能全部放入父代种群 $C_{i+1}$ ；
②将该层个体根据拥挤度从大到小排列，依次放入父代种群 $C_{i+1}$ 中，直到父代种群 $C_{i+1}$ 填满。

1.5 实数编码的交叉操作（SBX）

模拟二进制交叉：
$x _{1j}(t)=0.5×[(1+γ_j ) x_{1j}(t)+(1-γ_j ) x_{2j} (t)]$
$x _{2j} (t)=0.5×[(1-γ_j ) x_{1j}(t)+(1+γ_j ) x_{2j}(t)]$
其中
$γ_j=\left\{\begin{matrix}(2u_j)^{1/(η+1)}\;\;\;\;\;\;\;\;\;\;\;\;u_j<0.5 \\ (1/(2(1-u_j))^{1/(η+1)}\;\;\;\;else \end{matrix}\right.$

1.6 多项式变异（polynomial mutation）

多项式变异：
$x _{1j} (t)=x_{1j} (t)+∆_j$
其中
$∆_j=\left\{\begin{matrix}(2u_j)^{1/(η+1)}-1\;\;\;\;\;\;\;\;\;\;\;\;u_j<0.5 \\ (1-(2(1-u_j))^{1/(η+1)}\;\;\;\;else \end{matrix}\right.$
并且0≤ $u_j$ ≤1。

2. 算法实现框图

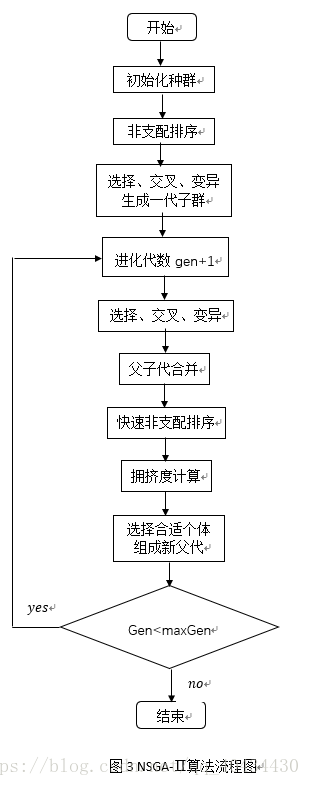
NSGA-Ⅱ算法的基本思想为：首先，随机产生规模为N的初始种群，非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；其次，从第二代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群：依此类推，直到满足程序结束的条件。该算法的流程图如图3所示。
NSGA-Ⅱ算法流程图

扫描二维码关注公众号，回复： 3419779 查看本文章

3. 实验结果

本文使用实数编码的模拟二进制交叉和多项式变异，交叉概率 $p_c=0.9$ ，变异概率 $p_m=1/n$ ， $η_c=20$ ， $η_m=20$ 。以下为选取的5个非凸非均匀的多目标函数的运行结果如图4到图8所示。

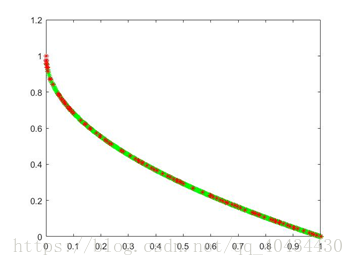
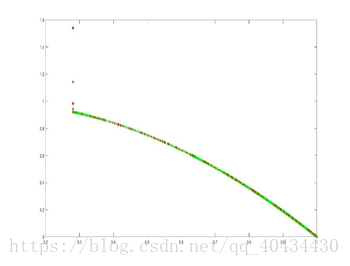
3.1 ZDT1

$f_1=x_1$
$g=1+9((∑_{i=2}^nx_i )/(n-1))$
$f_2=g(1-(f_1/g)^{0.5} ).n=30,x_i∈[0,1]$
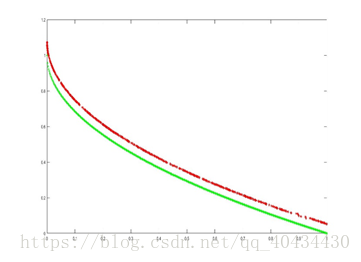
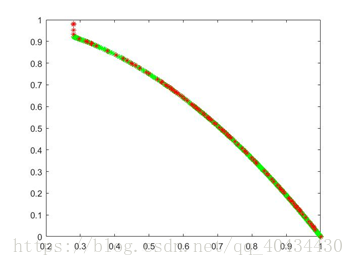
选取种群大小为500，迭代次数500次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图4(上)所示。
选取种群大小为100，迭代次数2000次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图4(下)所示。
在这里插入图片描述

图4 ZDT1 pareto最优解对比图（绿色为理论值，红色为实验值）

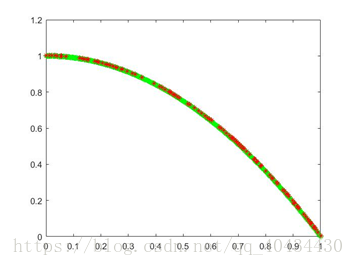
3.2 ZDT2

$f_1=x_1$
$g=1+9((∑_{i=2}^n x_i )/(n-1))$
$f_2=g(1-(f_1/g)^2 ).n=30,x_i∈[0,1]$
选取种群大小为500，迭代次数500次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图5（上）所示。
选取种群大小为100，迭代次数2000次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图5（下）所示。
在这里插入图片描述

图5 ZDT2 pareto最优解对比图（绿色为理论值，红色为实验值）

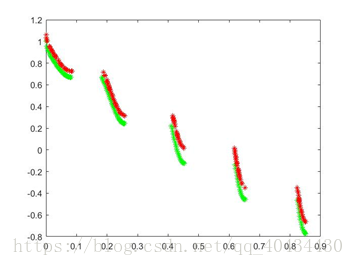
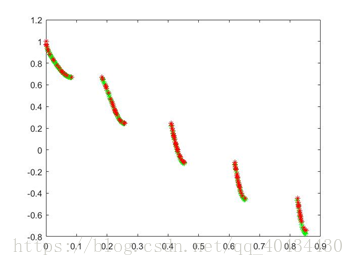
3.3 ZDT3

$f_1=x_1$
$g=1+9((∑_{i=2}^nx_i )/(n-1))$
$f_2=g(1-(f_1/g)^{0.5}-(f_1/g)sin⁡(10πf_1)).n=30,x_i∈[0,1]$
选取种群大小为136，迭代次数500次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图6示。
选取种群大小为136，迭代次数2000次，pc=0.9,pm=1/30,ηc=20,ηm=20,得到结果如图6示。
在这里插入图片描述

图6 ZDT3 pareto最优解对比图（绿色为理论值，红色为实验值）

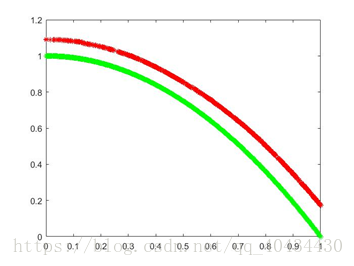
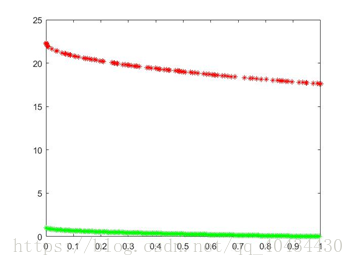
3.4 ZDT4

$f_1=x_1$
$g=1+9*10+∑_{i=2}^n( (x_i )^2-10cos⁡(4πx_i))$
$f_2=g(1-(f_1/g)^{0.5} ).n=10,x_1∈[0,1];x_(2…6)∈[-5,5]$
选取种群大小为100，迭代次数500次，pc=0.9,pm=0.1,ηc=20,ηm=10,得到结果如图7（上）所示。
选取种群大小为100，迭代次数2000次，pc=0.9,pm=0.1,ηc=20,ηm=10,得到结果如图7（下）所示。
在这里插入图片描述

图7 ZDT4 pareto最优解对比图（绿色为理论值，红色为实验值）

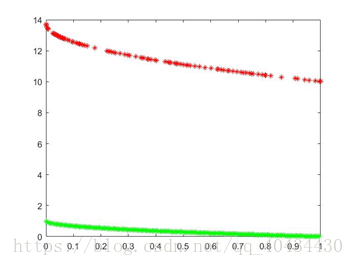
3.5 ZDT6

$f_1=1-e^{-4x_1} sin^6 (6πx_1)$
$g=1+9((∑_{i=2}^nx_i )/(n-1))^{0.25}$
$f_2=g(1-(f_1/g)^2 ).n=10,x_i∈[0,1]$
选取种群大小为100，迭代次数500次，pc=0.9,pm=0.1,ηc=20,ηm=20,得到结果如图8（上）所示。
选取种群大小为100，迭代次数2000次，pc=0.9,pm=0.1,ηc=20,ηm=20,得到结果如图8（下）所示。
在这里插入图片描述

图8 ZDT6 pareto最优解对比图（绿色为理论值，红色为实验值）
从结果中可以看出，除ZDT4以外，找到的解几乎全部是pareto前端上的点，并且解在目标空间上分布十分均匀，该算法对于非凸非均匀的多目标函数最优解的寻找还是十分有效的。由于ZDT4具有许多局部pareto最优前沿，为了摆脱这些局部前沿，需要对决策向量进行大的改变，因此选取ηm=10，但仍离真正的pareto前沿还有很大的差距。

3.6 对比

表1 γ的均值和方差（500代）

项目	ZDT1	ZDT2	ZDT3	ZDT4	ZDT6
均值	0.0532	0.0972	0.1712	20.2304	0.3284
方差	0.0021	0.0051	0.0048	0.6310	0.0109

表2 Δ的均值和方差（500代）

项目	ZDT1	ZDT2	ZDT3	ZDT4	ZDT6
均值	0.4575	0.4615	0.6640	0.5203	0.9538
方差	0.0021	0.0015	0.0030	0.0013	0.0055

表3 γ的均值和方差（2000代）

项目	ZDT1	ZDT2	ZDT3	ZDT4	ZDT6
均值	0.0011	0.0027	0.0225	12.0341	0.2092
方差	0.0002	0.0002	0.0005	0.3320	0.0021

表4 Δ的均值和方差（2000代）

项目	ZDT1	ZDT2	ZDT3	ZDT4	ZDT6
均值	0.4478	0.4337	0.6586	0.5168	0.4529
方差	0.0001	0.0003	0.0006	0.0018	0.0001

根据上述实验数据，进行五组实验，计算distance metric γ，diversity metric Δ的均值和方差，迭代500次后得到结果如表格1-2所示。迭代2000次后得到的结果如表格3-4所示。
      表1显示了NSGA-Ⅱ（实数编码500代）在5个问题上运行获得的distance metric γ的均值和方差，实验结果表明，除了ZDT4和ZDT6以外的问题均取得了良好的收敛效果，除ZDT4以外，其他问题5次运行结果的差异也都很小。
      表2显示了NSGA-Ⅱ（实数编码500代）在5个问题上运行获得的diversity metric Δ的均值和方差，实验结果表明，NSGA-Ⅱ在上述问题上均具有较强的传播多样性，并且5次运行结果的差异都很小。
      像500代的时候一样保留所有其他参数，但将代数增加至2000代，得到表3的distance metric γ的均值和方差以及表4的diversity metric Δ的均值和方差。将表3表4与表1表2对比可知，5个问题的distance metric γ随着代数的增加都有改善，其中ZDT3和ZDT4的改善尤为显著，除此之外，因为在500代时问题的结果已经有了良好的多样性分布了，所以代数的增加并没有对diversity metric Δ产生巨大的影响。
完整代码加注释见百度云链接：
链接：https://pan.baidu.com/s/1cp1Ig3Qfl0YDbtGtd2NeuQ
密码：3izh
[1]:Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.