MOEA/D学习笔记

阅读文献：MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition
中文翻译版本：https://download.csdn.net/download/qq_36317312/12597149

简介

基于分解的多目标算法首先是2007年由Qingfu Zhang等人提出。主要思想是将一个多目标优化问题分解为若干个标量优化子问题，并同时对它们进行优化。每个子问题只利用相邻的几个子问题的信息进行优化，使得MOEA/D算法在每一代的计算复杂度都低于MOGLS和非支配排序遗传算法II(NSGA-II)。

Introduction

多目标优化问题的数学模型一般可以写成如下形式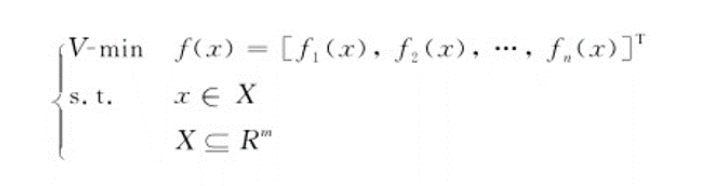
其中f_i (x)(1≤i≤n)表示n个目标函数，x⊆R^m 是其变量的约束集合，可以理解为变量的取值范围f_i的目标是相互矛盾的，因此用帕累托最优来权衡各个目标。
在许多多目标优化的实际应用中，决策者需要近似PF来选择最终的优选解（1.获取完整的PF 耗时。2.信息溢出，决策者可能对处理过多的帕累托最优向量不感兴趣）。
PF的近似可以分解为若干个标量目标优化子问题。这是许多用于逼近PF的传统数学规划方法背后的基本思想。现在有许多的聚合方法，最流行的是切比雪夫法和加权法。最近，边界交叉方法也引起了许多的关注。
MOEA/D特征

MOEA/D为将分解方法引入多目标进化计算提供了一种简单而有效的方法。通常在数学规划社区中开发的分解方法可以很容易地合并到MOEA/D框架中的EAS中，用于求解MOPS。
由于MOEA/D优化的是标量优化问题，而不是直接解决MOP的整体问题，因此在MOEA/D的框架下，给非分解MOEA带来困难的适应度分配和多样性维护等问题可以变得更容易处理。
与NSGA-II和MOGLS相比，MOEA/D在每一代都具有较低的计算复杂度。MOEA/D利用相邻子问题的解的信息去同时优化N标量子问题。相对来说，MOEA/D不会重复的优化标量子问题，因为它利用了子问题之间的协同进化机制，所以算法的计算复杂度比较低。
在MOEA/D中使用标量优化方法是非常自然的，因为每个解都与一个标量优化问题相关联。

多目标优化的分解算法

1.权重求和法

权重求和法最常用的聚合方法，假设待优化的多目标问题有M个总目标，该函数通过一个非负的权重向量λ =(λ1，λ2，⋯，λm) 加权到每个目标上将MOP转换为单目标子向量，数学表达式为：
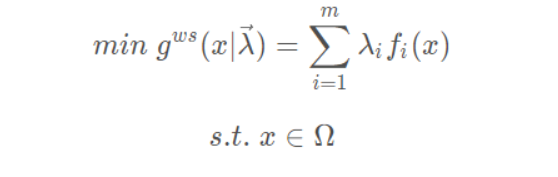
在这里插入图片描述
其中，向量λ =(λ1，λ2，⋯，λm) 是一组权重向量，每个权值分量λi 分别对应第i个目标向量，对于λ_i>=0且λ_i之和为1。

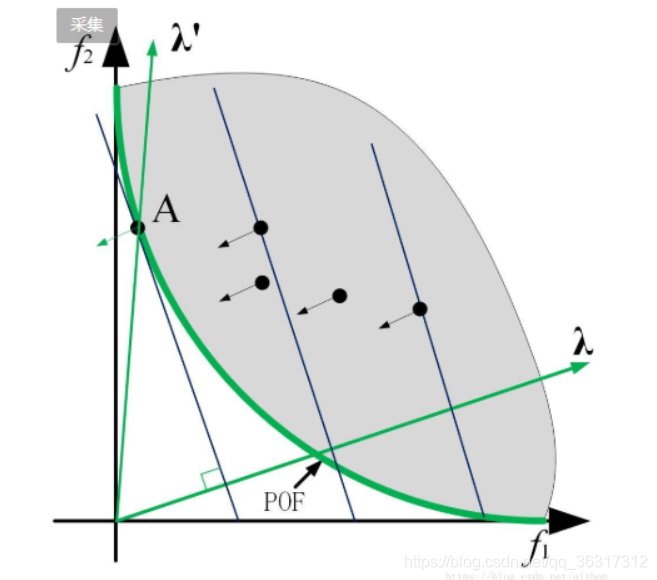
根据数学表达式λ_i*f_i可以看成点f_i在λ方向的投影，然后寻找最小值。通过图像分析，我们可以作几条等高线，就是垂直于λ的线，这样我们可以看从原点到直角点的距离就是f_i在λ方向的投影，因此很容易可以看出来，A点就是最短距离的点。同理，以此类推，找出最短距离的点，共同生成一组不同的帕累托最优向量。
但是权重求和法有限制，标准的权重求和法不能处理非凸问题，因为由上图可知，对于非凸问题，每个参照向量的垂线与其前沿不可能相切。

2.切比雪夫聚合方法

切比雪夫的数学表达式如下：
在这里插入图片描述
根据表达式可知找出λ_i(f_i(x)-z_i）的最大值，为什么需要取得最大值？
我们可以这样想，数值越大说明什么呢？说明在这个目标函数上离理想点越远。假设λ₁(f₁(x)-z₁）是比较大的值，我们逐渐改变x，让这个值离z越来越近，直到到达Pareto front上对应的点为止。这个过程其实就是在求这个函数g(x)=λ₁(f₁(x)-z₁）的最小值。如果连这个较大的λ₁(f₁(x)-z₁）都达到了它的最小值了，那么其它λ_i*(f_i(x)-z_i）也会到达最大值。
下面我们将从图像方面来进行讲解
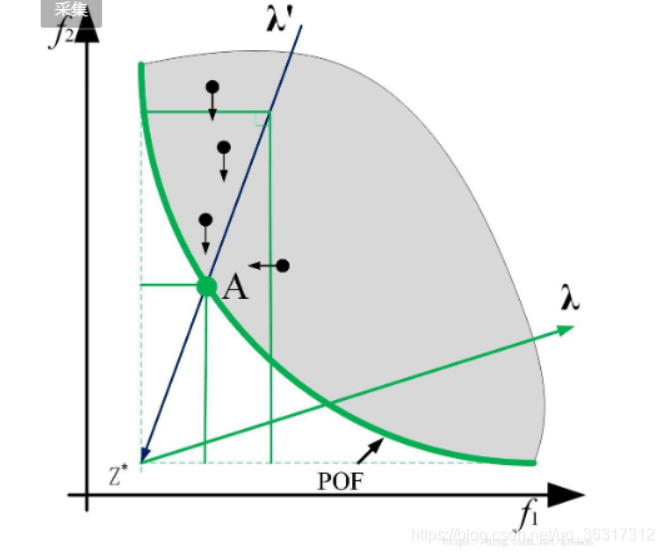
在这里插入图片描述

第一种理解方式
以二目标最小优化问题为例，我们令w_i=(f_i(x)-z_i）,如图所示，坐标轴进行了相关的平移，最终以虚线为平移后的坐标系，横坐标为w₂，纵坐标为W₁。我们给定一个向量λ_i，根据图中蓝线所示，我们的目标就是要找到Pareto前沿面PF（绿色加粗的线）上的个体点。给定向量λ_i之后，对于位于λ上方的个体有w₁λ₁>w₂λ₁(可以根据移位比较斜率)，因此无论w2的取值如何变化，只要w₁不变，那么结果大小都一样，min值=w₁λ₁，所以等高线是平行于w₂，同理可知，位于λ下方的等高线是平行于w₁的。（正如图中绿色细线所示的那样，为等高线）。
第二种理解方式
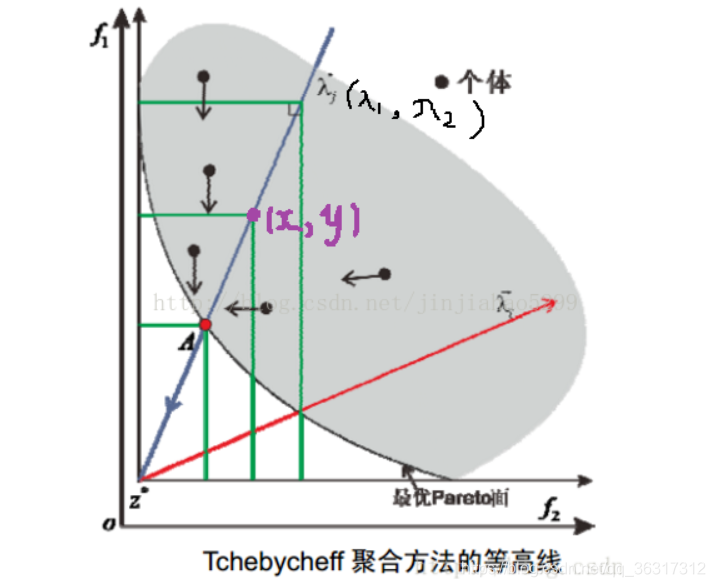
在这里插入图片描述
单看f1函数，即只考虑纵坐标，若两点等值，必然是λ_i*(f_i(x)-z_i）式中f1的函数值相等（因为另外两个量是不变的），即纵坐标相等，所以f1函数的等高线是一组平行于横轴的直线。f2类似，为一组平行于纵轴的直线。

通过上述两种理解讲解了等高线是由两条垂直的线组成，我们继续介绍下面的收敛过程，对于位于λ上方的个体，如果出现新个体w₁小于等高线值，则等高线向下移动（注意是两条线同时移动）；同理，位于λ下方的个体，如果出现新个体w₂小于等高线值，则等高线向左移动（注意是两条线同时移动），直到搜索到Pareto前沿。我们可以看上面两张图片，它们所指的箭头就是向下，向左的方向。
当我们对向量λ取不同的值，就可以得到其他Pareto解。
最后文章中还提及了切比权重聚合方法，就是结合两种方法并加了个参数p控制两种方法的比例。
在这里插入图片描述

3.边界交叉聚合方法

在几何中，边界交叉法就是找到最上边界和一组线的交点。如果这些线在均匀分布，则可以预期所得到的交叉点提供整个PF的良好近似。下面给出数学表达式：
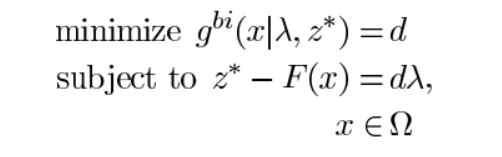
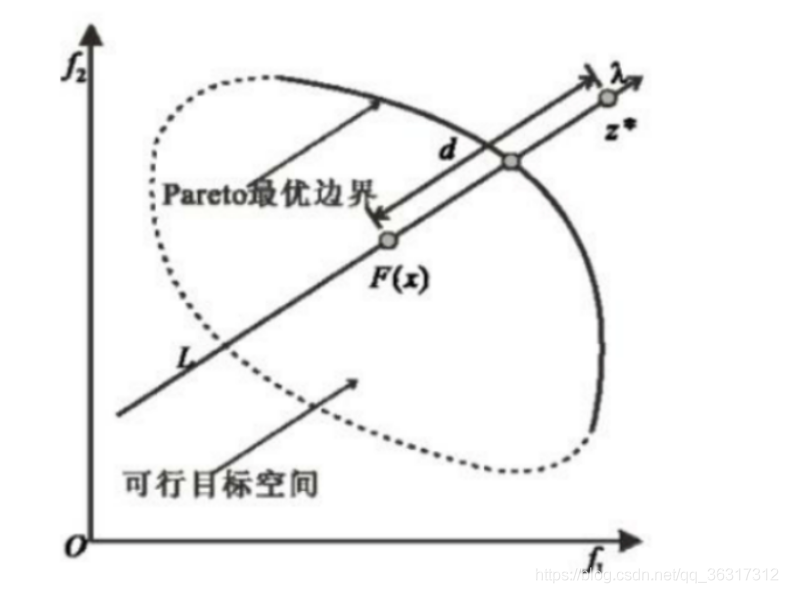
在这里插入图片描述

式子中等式约束其目的是为了保证F(x)位于权重向量λ的方向上，通过减小d来使算法求出的解逼近PF。但该条件不太容易实现，故将其改进为下边这种方法。

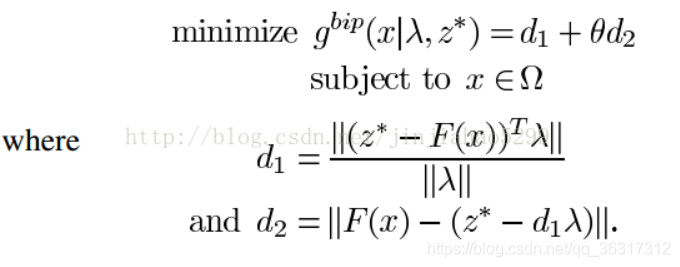
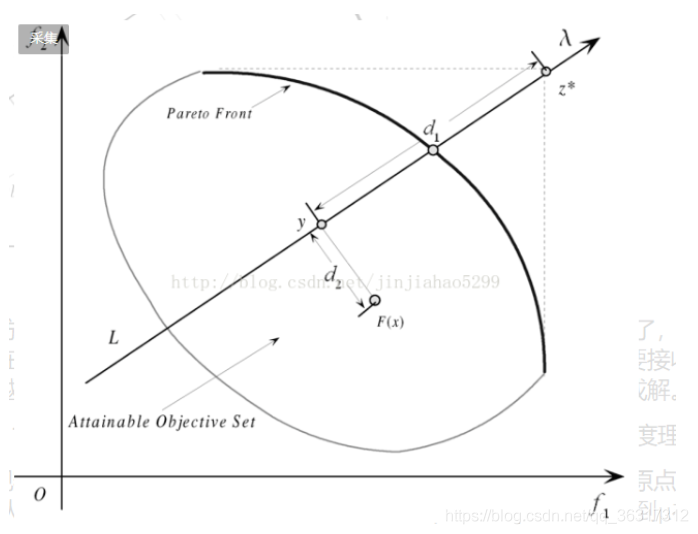
可知算法放宽了对算法求出的解得要求，但加入了一个惩罚措施，说白了，就是你可以不把解生成在权重向量的方向上，但如果不在权重向量方向上，你就必须要接收惩罚，你距离权重向量越远，受的惩罚越厉害，以此来约束算法向权重向量的方向生成解。
接下来是关于d1和d2两个参数的计算表达式的含义说明，我依然是从几何角度理解的。
在这里插入图片描述
d1——观察d1的计算表达式，Z*-F(x)可以看做原点到Z点的向量减去原点到F(x)的向量，得到的是从F(x)出发指向Z的一个向量，暂且命名为μ，之后μ与λ相乘得到μ在λ方向上的投影，这个长度值与λ的长度值之比为d1。
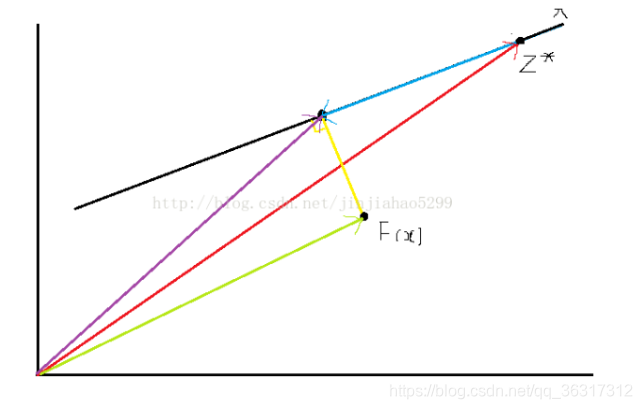
d2——其表达式的含义其实也无非就是利用向量运算构造出d2所表示的向量，取模即可得到d2.构造过程如下：
Z表红色向量，d1λ表蓝色向量（因为减法，所以方向取反），红色减蓝色得紫色向量，F(x)表绿色向量，绿色减紫色得黄色向量，即d2表黄色向量的长度。

MOEA/D的框架

整体框架

令λ1,…,λN为一组均匀分布的权重向量。通过使用切比雪夫法，可以将PF近似的问题分解为标量优化子问题，第j个子问题的目标函数是
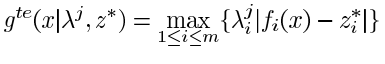
在这里插入图片描述
在一次运行中，MOEAD同时优化所有的N个目标。
在每次迭代中，应维持的一些：

大小为N的种群,x¹,…x^N，xⁱ表示第i个子问题的当前解；
FV¹,…,FV^N，FVⁱ=F(xⁱ)；
z_i表示目标函数f_i(x)当前找到的最优值(最大值) ；
一个外部种群（EP），用来保存非支配解；

算法流程

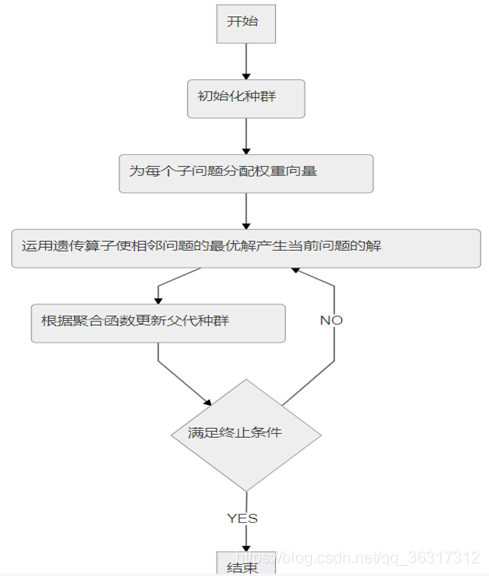
在这里插入图片描述

STEP1:初始化

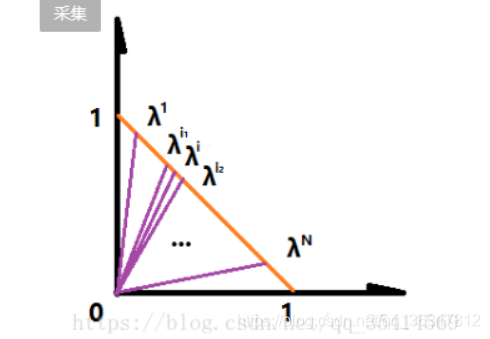
1)计算权重向量之间的欧式距离，对于每个权重向量λ得到离它最近的T个权重向量存在B(i)，所以向量终端一定在橙线（y=−x+1 y=-x+1y=−x+1）上，所以欧式距离越小，表示越相邻；
在这里插入图片描述
2）随机生成初始种群

4）EP–>外部种群

SETP2:种群更新
SETP3:结束

实验结论

最终实验结果：
1.在多目标0-1背包问题和连续多目标优化问题上，MOEA/D以简单的分解方法优于或接近于MOGLS和NSGA-II。
2.使用目标归一化的MOEA/D可以处理不同规模的目标，采用高级分解方法的MOEA/D可以为3个目标测试实例生成一组分布非常均匀的解。
3.对MOEA/D在小种群情况下的能力、MOEA/D的可扩展性和灵敏度进行了实验研究。

ps：初学多目标进化算法，也是看了很多大佬的博客以及原文进行理解总结，如果有一些不对的地方还请大佬们进行批评指正，同时也借鉴了这些博客，如果想要深入了解，可以看下面博客。
https://blog.csdn.net/sinat_33231573/article/details/80271801
https://blog.csdn.net/loveC__/article/details/86624177
https://blog.csdn.net/qithon/article/details/72885053
https://blog.csdn.net/qq_35414569/article/details/79655400
https://blog.csdn.net/qithon/article/details/72885053

多目标优化--MOEAD算法笔记