【计算机图形学】3D引擎几何学基础 (直线、平面、视锥)

1.1 参数化表达式

1.1.1 直线

假设3D空间中有两点 P1 和 P2，通过该两点所在的直线的参数化表达式为：

$\small P(t)=P1+ t*(P2-P1)=(1-t)*P1+t*P2$

可以理解为，过P1和P2两点的直线上的点，都是从P1点出发，沿着P2-P1的矢量方向可以找到的

这里，t可以是任意实数，若t为0到1之间，则表示的是连接 P1 和 P2 的线段，即P(t)点位于两点之间

1.1.2 射线

假设射线的端点为 S，且沿着某一方向 V 无限延伸，射线的参数化表达式为：

$\small P(t)=S+t*V$

这里，t 是大于等于 0 的实数

该式也可以用来表示直线，如果令 $\small \mathrm{S = P1}$ ， $\small \mathrm{V = P2 - P1}$ ，该式与直线方程相同

1.2 点与直线的距离

1.2.1向量投影

如图所示，由向量P和向量Q，求向量P在向量Q上的投影，计算方法如下：

我们可以将向量P当做一个直角三角形的斜边，那么投影大小就是 $\small \left \| P \right \|\cdot \cos \alpha$

但是去直接计算 $\small \alpha$ 的值还是比较麻烦的，换个简单点的：

根据公式可得： $\small P\cdot Q = \left \| P \right \|\cdot \left \| Q \right \|\cdot \cos \alpha$ ，则： $\small \left \| P \right \|\cdot \cos \alpha =\frac{P\cdot Q}{\left \| Q \right \|}$

即投影大小也等于 $\small \frac{P\cdot Q}{\left \| Q \right \|}$ ，当然，这里的求得的值是一个不带方向的标量

如果想求矢量呢？即求大小为 $\small \frac{P\cdot Q}{\left \| Q \right \|}$ ，方向与向量Q平行的矢量：

由 $\small Q/\left \| Q \right \|$ 可以获得向量Q的单位矢量，那么向量P在向量Q上的投影 $\small proj_QP$ 可以表示为：

$\small proj_QP =\frac{P\cdot Q}{\left \| Q \right \|^{2}}\cdot Q$

顺便一提，向量P相对于向量Q的垂直向量可表示为：

$\small perp_QP =P-proj_QP$

1.2.1 点到直线的距离计算

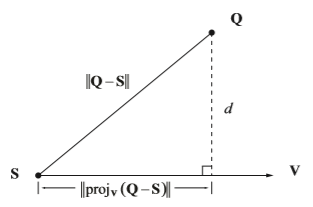
如图所示，已知由端点S和方向V定义的直线，和一点P，求点P到直线的距离d：

根据勾股定理可知：

$\small d^{2} =(Q-S)^{2} - [ proj_v(Q-S)]^{2}$

$\small d^{2} =(Q-S)^{2} - [\frac{(Q-S)\cdot V}{\left \| V \right \|^{2}}\cdot V]^{2}$

即点Q到直线的距离，等于Q-S的平方减去Q-S在方向V上的投影的平方

对上式简化可得：

$\small \mathbf{ }d=$$\sqrt[]{(Q-S) - [\frac{(Q-S)\cdot V}{\left \| V \right \|^{2}}\cdot V]^{2} }$$$

1.3 直线间的距离

在二维空间中，两条直线，要么平行，要么相交于一点。在三维空间中，还存在一种情况，即两条直线既不相交也不平行，我们称之为扭曲。下面将通过简单计算，获取两条相扭曲的直线上两点之间的最近距离。

如上图所示，假设有两条直线，其参数化方程分别为：

$P_1(t_1) = S_1+t_1\ast V_1$

$P_2(t_2) = S_2+t_2\ast V_2$

那么求两条直线上两点之间的最近距离，就是求 $\left \| P_1(t_1)-P_2(t_2) \right \|$ 的最小值，设：

$f(t_1,t_2) = \left \| P_1(t_1)-P_2(t_2) \right \|^{2}$

展开平方，并且将 $P_1(t_1)$ 和 $P_2(t_2)$ 的表达式带入方程，暴力求解，得到：

$f(t_1,t_2) = S_1^{2}+t_1^{2}V_1^{2}+2 t_1 S_1\cdot V_1+S_2^{2}+t_2^{2}V_2^{2}+2 t_2 S_2\cdot V_2- 2(S_1\cdot S_2+t_1V_1\cdot S_2+t_2V_2\cdot S_1+t_1t_2V_1\cdot V_2)$

式子还挺长，不过可以通过分别令 $f$ 相对 $t_1$ 和 $t_2$ 的偏导数为0求解得到最小值：

$\small \frac{\partial f}{\partial t_1} = 2t_1V_1^{2}+2S_1\cdot V_1-2V_1\cdot S_2-2t_2V_1\cdot V_2 = 0$

$\small \frac{\partial f}{\partial t_2} = 2t_2V_2^{2}+2S_2\cdot V_2-2V_2\cdot S_1-2t_1V_1\cdot V_2 = 0$

消去2，上述两个等式整理后，可写成矩阵形式：

$\small \begin{bmatrix} V_1^{2} & -V_1\cdot V_2\\V_1\cdot V_2 & -V_2^{2} \end{bmatrix}\begin{bmatrix} t_1\\t_2 \end{bmatrix} = \begin{bmatrix} (S_2-S_1)\cdot V_1\\ (S_2-S_1)\cdot V_2 \end{bmatrix}$

解关于 $\small t_1$ 和 $\small t_2$ 的方程得：

$\small \begin{bmatrix} t_1\\t_2 \end{bmatrix} = \begin{bmatrix} V_1^{2} & -V_1\cdot V_2\\V_1\cdot V_2 & -V_2^{2} \end{bmatrix}^{-1} \begin{bmatrix} (S_2-S_1)\cdot V_1\\ (S_2-S_1)\cdot V_2 \end{bmatrix}$

$\small = \frac{1}{(V_1\cdot V_2)^{2}-V_1^{2}V_2^{2}} \begin{bmatrix} -V_2^{2} & V_1\cdot V_2\\-V_1\cdot V_2 & V_1^{2} \end{bmatrix} \begin{bmatrix} (S_2-S_1)\cdot V_1\\ (S_2-S_1)\cdot V_2 \end{bmatrix}$

根据上式可以求得 $t_1$ 和 $t_2$ 的值，代入函数 $f(t_1,t_2)$ 可以求得两条直线之间的最短距离的平方，再开方。或者代入两条直线的参数化方程，求得两条直线上距离最近的两个点，再求两点间的距离。

如果方向向量 $V_1$ 和 $V_2$ 是单位向量，则 $V_1^{2} = V_2^{2} = 1$ ，能进一步简化式子。

如果 $\small (V_1\cdot V_2)^{2}-V_1^{2}V_2^{2}$ 的值等于0，说明方程无解，则两条直线平行。此时两条直线间的距离等于一条直线上任意一点到另一条直线的距离。

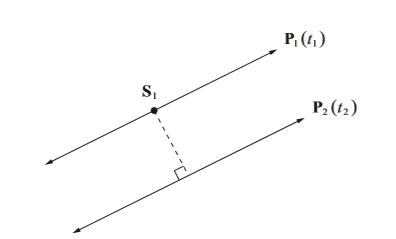
如下图所示，点 $\small S_1$ 到直线 $\small P_2(t_2)$ 的距离，就是两条直线间的距离。

二、三维空间中的平面

2.1 参数化表达式

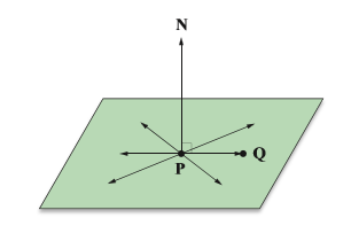
已知一个三维点 P 与法向量 N，设过点 P 且与 N 垂直的平面为点 Q 的合集，那么 Q 满足：

$N\cdot (Q-P)=0$

除此之外，平面方程还有一种常用的表达方式：

$Ax+By+Cz+D=0$

这里的 A，B，C 其实就是法向量 N 的 x，y，z 分量，而 $D=-N\cdot P$

2.2 点到平面的距离

对于平面S1,有方程Ax+By+Cz+D=0，之前已经提到了，D = -N·P，N为平面的法向量，P是平面S1上一点。

因为N是向量，P是一个点，可以先把N·P看做是向量N和向量OP的乘积(O=(0,0,0)为原点)，以下描述和公式中的向量P皆指代向量OP。

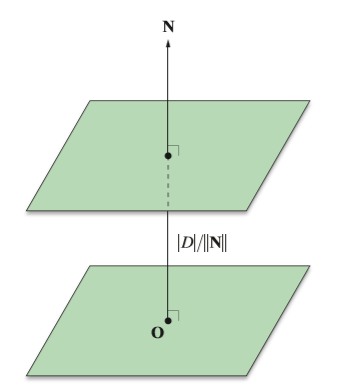
设过原点O与S1平行的平面为S0，因为 $D=-N\cdot P$

$N\cdot P=|N||P|\cos \theta$ ， $\theta$ 为向量N和向量P的夹角， $|P|\cos \theta$ 是向量P在法线向量N上的投影的矢量大小，也是S0和S1的之间的距离，即 $\left \| P \right \|\cos \theta =\frac{N\cdot P}{\left \| N \right \|}=\frac{|D|}{\left \| N \right \|}$ 为S0和S1的之间的距离。

同理，设任意一点R，假设过点R且与平面S1，S0平行的平面为S2，则S0和S2之间的距离d2为 $\left \| R \right \|\cos \alpha = \frac{ N\cdot R}{ \left \| N \right \|}$

若平面法向量N为单位向量，则点R到平面S1的距离为S0和S1之间的距离减去S0和S2之间的距离，即：

$d=N\cdot Q+D$

若d=0，则点R位于平面上；

若d>0，则点R位于平面法向量所指的一侧，称为平面的正向侧

若d<0，则点R位于平面的负向侧

2.3 直线和平面的交点

求一条直线和一个平面的交点是3D图形引擎中的普通计算，比如说在多边形裁剪中被广泛使用。

设过点S且与方向V平行的直线的表达式为： $P(t)=S+tV$

设有一法向量为N且到原点的符号距离为D的平面，那么则存在：

$N\cdot P(t)+D = 0$

即存在P(t)直线过该平面的一点(当然也可能直线和平面平行了，没有交点)

解上述关于P(t)的方程，即可获得直线与平面的交点。将P(t)替换为 $S+tV$ ，可得：

$N\cdot S+(N\cdot V)t +D = 0$

求解关于t的方程，可得：

$t=\frac{-(N\cdot S+D)}{N\cdot V}$

将t的值代入直线方程即可求得交点。

如果 $N\cdot V=0$ ，则直线与平面平行，平面法向量N与直线方向向量V垂直，此时，若 $N\cdot S+D=0$ ，则直线位于平面上，否则无交点。

2.4 三个平面斜交

一个空间的区域通常表示成由一系列平面为边界组成的凸面多面体的形式。该多面体的边和顶点可以通过执行多次三个平面的求交运算得出。

2.4.1 求三个平面交于一点

设 $L_1=<N_1,D_1>$ ， $L_2=<N_2,D_2>$ ， $L_3=<N_3,D_3>$ ，为任意三个平面

通过计算以下方程组的解可以得到同时位于这三个平面的点Q：

$L_1\cdot Q=0$

$L_2\cdot Q=0$

$L_3\cdot Q=0$

写成矩阵形式：

$MQ=\begin{bmatrix} -D_1\\-D_2 \\ -D_3 \end{bmatrix}$

其中，矩阵M的表达式如下：

$M=\begin{bmatrix} (N_1)_x & (N_1)_y& (N_1)_z \\ (N_2)_x & (N_2)_y& (N_2)_z \\ (N_3)_x & (N_3)_y& (N_3)_z \end{bmatrix}$

假设矩阵M可逆，计算下式可得到三个平面的唯一交点Q：

$Q=M^{-1}\begin{bmatrix} -D_1\\-D_2 \\ -D_3 \end{bmatrix}$

如果矩阵M是奇异矩阵，即行列式为0： $detM=0$ ，则这三个平面不相交与一点。当三个平面法向量位于同一平面时，会出现这种情况，下图所示就是情况之一：

2.4.2 求两个平面交于一条直线

设有两个不平行的平面 $L_1 = <N_1,D_1>$ 和 $L_2 = <N_2,D_2>$ 相交时，其交于一条直线，如下图所示：

交线的方向V与两个平面的法向量都垂直，可表示为 $V=N_1\times N_2$ 。

已知交线的方向，为了完整获取表达式，还需要知道直线上的一点。

为此，构造经过原点，且法向量为V的第三个平面 $L_3= <V,0>$ ，这可以确保三个平面交于一点，该点即为平面 $L_1$ 和 $L_2$ 上的一点。

利用之前推倒的求三个平面的唯一交点的公式，可以得到交点Q:

$Q=\begin{bmatrix} (N_1)_x &(N_1)_y &(N_1)_z \\ (N_2)_x& (N_2)_y & (N_2)_z\\ V_x& V_y & V_z \end{bmatrix}^{-1}\begin{bmatrix} -D_1\\-D_2 \\ 0 \end{bmatrix}$

则平面 $L_1$ 和 $L_2$ 交线的表达式为 $P(t) = Q + tV$ 。

三、视锥

3.1 定义

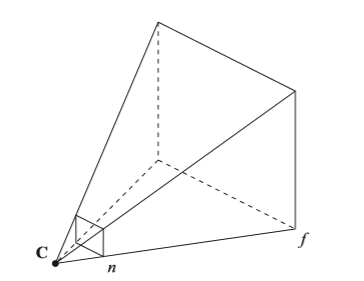
在三维场景中，不是所有物体都能够被“看”见的，只有位于视椎体内的物体才会被渲染并可见。如下图所示，视椎体的形状像一个四棱锥，其顶点位于虚拟相机，可以想象它是观察三维场景的眼睛，而视椎体的范围大小就是可观察的范围大小。

视椎体由六个平面组成，其中最重要的两个平面是近锥平面和远锥平面，这两个平面定义了场景中的对象对相机可见的最近和最远距离，因此椎体顶点到近裁剪平面的那段空间内的物体也是不会被渲染的。

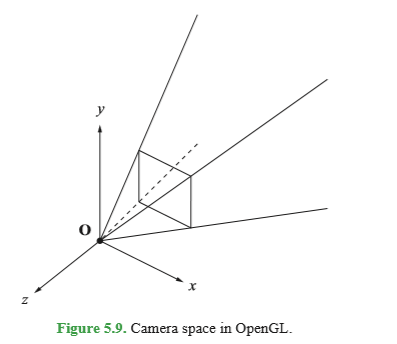
相机空间，也称观察空间，其坐标原点位于视椎体的顶点，x轴向右，y轴向上，z轴方向与3D图形库有关。在OpenGL中，z轴的方向与相机指向相反（右手坐标系）；Direct3D中，z轴方向与相机指向相同（左手坐标系）。

3.2 视场

投影平面是一个与相机指向垂直的平面，设该平面与相机的距离为e，有时距离e也被称为焦距。

3.2.1 水平视场

如图为视椎体的俯视图，左锥面与右锥面分别与投影平面在 x = -1 和 x = 1 处相交。因此 e 与左锥面和右锥面之间的夹角 $\alpha$ 有关，夹角 $\alpha$ 被称为水平视场角。

对于给定的水平视场角 $\alpha$ ，求视椎顶点到投影平面的距离 e 为：

$e = \frac{1}{\tan (\alpha /2)}$

3.2.2 垂直视场

如图为视椎体的侧视图，要求得 $\beta$ ，则需要知道y的值。因为大多数显示器不是正方形而是长方形，所以垂直视场不等于水平视场。假设已知屏幕的宽高比为a（即显示屏幕的高度除以宽度，如像素分辨率为640*480的显示器的宽高比为0.75），那么底锥平面与顶锥平面与投影平面在 y = ±a 处相交。

垂直视场角 $\beta$ 的表达式如下：

$\beta = 2\ast \tan^{-1}\frac{a}{e}$

综上，视椎的4个边平面从投影平面切出一个长方形，该长方形与相机距离为 e,它的四条边分别位于 x=±1 和 y=±a 处。