前言:
在数学上,直线上的点有无穷多个。担当在计算机光栅显示器屏幕上表示这条直线时需要做一些处理。
为了在光栅显示器上用这些离散的像素点逼近这条直线,需要知道这些像素点的x,y坐标。
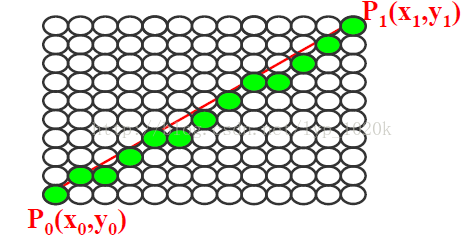
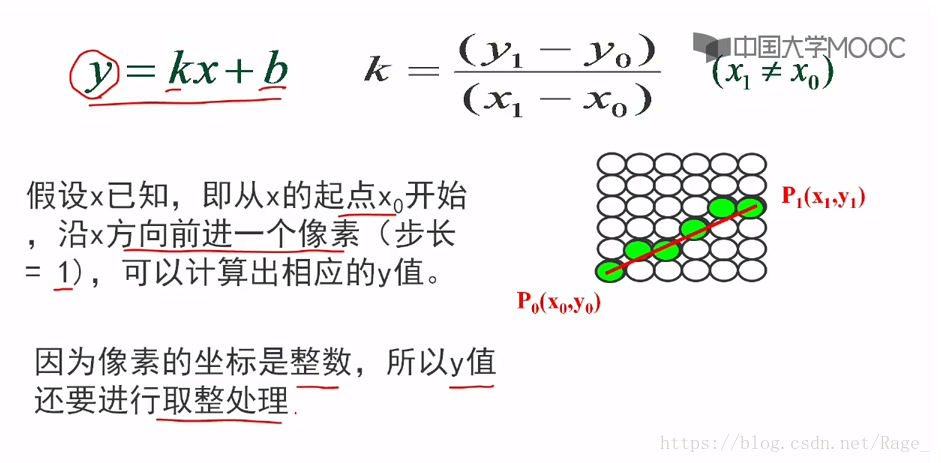
求出过p0,p1的直线段方程:y=kx+b; k=(y1-y0)/(x1-x0)(x1 ≠ x0)
假设x已知,即从x的起点x0开始,沿x方向前进一个像素(步长=1),可以计算出相应的y值。因为像素的坐标时整数,所以y值还要进行取整处理
如:p(1.7,0.8)取整为p(1,0)而1.7和0.8分别离2和1较近,所以可以先将坐标+0.5再取整
直线时最基本的图形,一个动画或真实感图形往往需要调用成千上万次画线程序,因此直线算法的好坏将直接影响图形的质量和显示速度。
直线的三种扫描转换算法:
- 数值微分算法(Digital Differential Analyzer,简称DDA)
- 中点画线法
- Bresenham算法
数值微分法DDA(Digital DIfferential Analyer):
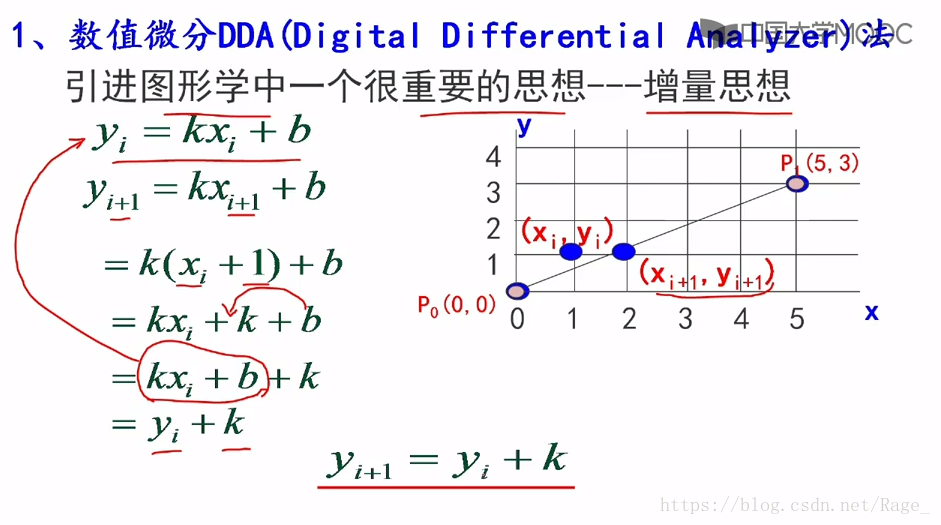
引进图形学中一个很重要的思想——增量思想
这个算法采用的是直线的斜截式方程(y=kx+b)。要求先算出直线的斜率,然后从起点开始,确定最佳逼近于直线的y坐标。假设起点的坐标为整数,直线方程为y=kx+b,k的取值在0到1之间,x每递增1,y相应地递增k。
这里需要处理的是:像素的坐标都是整数,x每次加1,y值必须是整数才行,所以这里要进行取整处理。如果采用+0.5进行出来,是可以达到效果,但是直线是最基本的图形,一个动画或者图形往往要调用上万次直线处理,所以相率十分低下。
此时,y=kx+b ,是通过一个乘法,再一个加法,再进行取整处理,才能画出这条直线。在计算机中,加减乘除,最快的是加法运算,如果能把乘法运算取消的话,只剩加法运算,效率会大大提高!所以如果把乘法取消掉呢?那就是增量思想。
推导如下:
最终:yi+1 = kxi+1 + b。
式子的含义是:当前步的y值等于前一步的y值加上斜率k。这样就把原来一个乘法和加法变成了一个加法!
我们用DDA算法实验一个例子:
首先计算K值,为0.6。0.6小于1。
下一次,x+1,新的y值为前一个y值+k: 0+0.6,进行四舍五入处理再加0.5取舍,为(0+0.6+0.5=1.1,四舍五入)1。
以此类推。。
DDA算法缺陷:
当|k|大于1的情况下:此时例子如下:
如果在绝对值k大于1的情况下,出现的情况是光栅点太稀疏了!我们表达一个点,要足够多的点,这样才看上去会是一条直线,而此时用DDA算法,光栅点太稀疏了!
-------------------------
DDA算法是否是最优呢?不是最优,如何改进呢?
第一个思路:计算机中,整数运算速度大于浮点运算速度,DDA算法是浮点加法,我们能否改进为整数加法呢??!
第二个思路:从直线方程上面类型做文章!下面就是中点画线法!
中点画线法
中点画线法采用一般是方程。
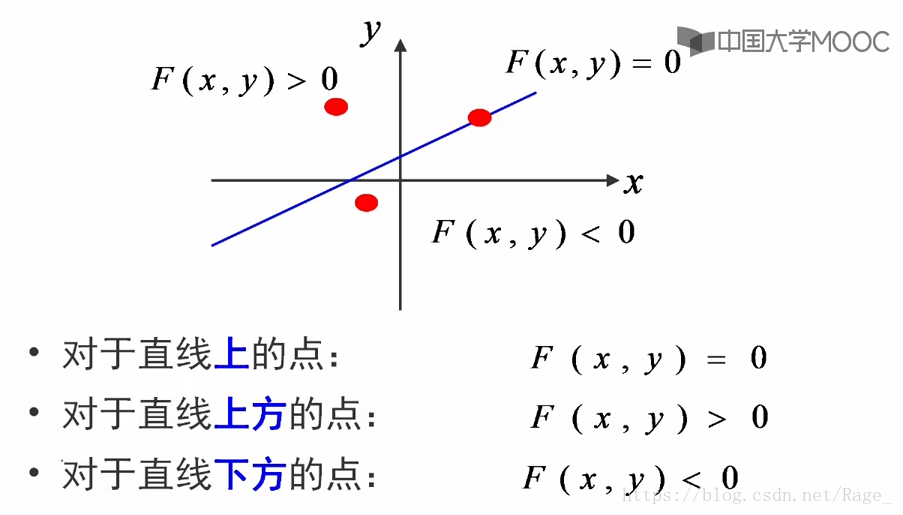
首先,给一个点F(x,y),用直线方程来说,对于直线的点,如果F(x,y)在直线上,则为0;如果F(x,y)直线上方则大于0;如果F(x,y)在直线下方则小于0.
所以中点画线法的基本原理是:直线在x方向增加一个单位,则在y方向上的增量只能是0和1之间。
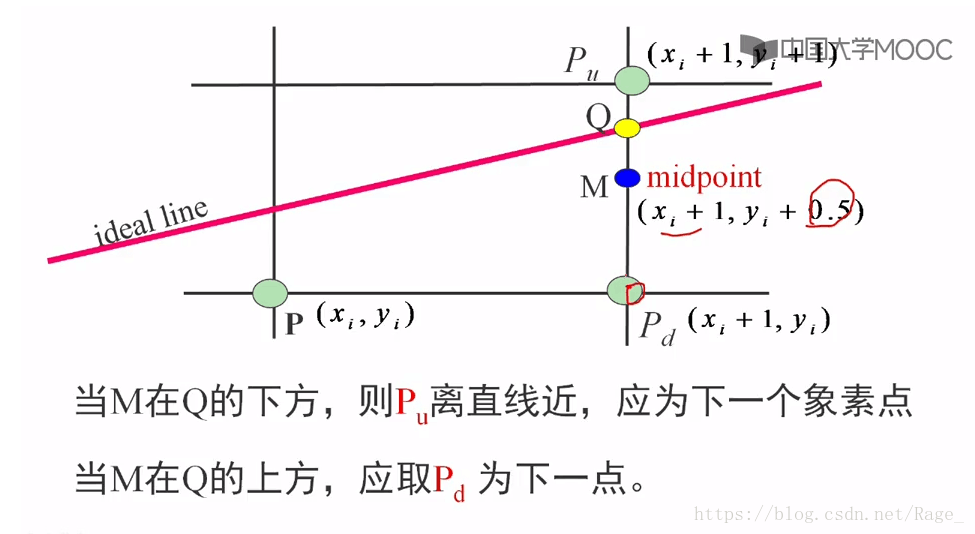
如上图:ideal line为理想直线。仍然是x+1,确定y的值。
M(xp + 1, yp + 0.5) 表示P1和P2的中点,Q是理想直线与垂直线x = xp + 1的交点,如果M点在Q点下方,很明显P2离直线更新一些,如果M在Q的上方,则P1离直线更新一些,我们取离直线最近的那个像素点,如果M和Q重合,我们约定取正右方的那个点。那么如何判断呢?即我们将M的坐标代入到直线的一般式方程。
假设起点和终点为 (x0, y0)和(x1, y1),则直线方程为:
F(x, y) = ax + by + c, 其中a = y0 - y1, b = x1 - x0,c = x0y1 - x1y0
对于直线上的点,F(x, y) = 0;直线上方的点,F(x, y) > 0;直线下方的点,F(x, y) < 0. 因此,判断M在Q的上方还是下方,只需将M点带入方程计算判别式:
d = F(M) = F(xp + 1, yp + 0.5) = a(xp + 1) + b(yp + 0.5) + c
对于每一个像素的判别式d,根据它的符号来判断下一个像素点。 由于d是xp和yp的线性函数,可采用增量计算来提高运算效率。
当d小于0,中点M在直线的下方,说明直线离上面的点近,取上方的点。
当d大于0,说明中点M在直线的上方,说明直线离下面的点近,取下方的点。
这就是中点直线画法的判别方式,y的值看d的大小,如图下:
好了,此时,我们看看此时中点划线算法的效率:
为了求出d,我们需要两个乘法,四个加法!
那么我们如何提高效率,能否和DDA算法一样,增量思想呢?完全可以!关键在于如果推导出d的递推公式!
如下:
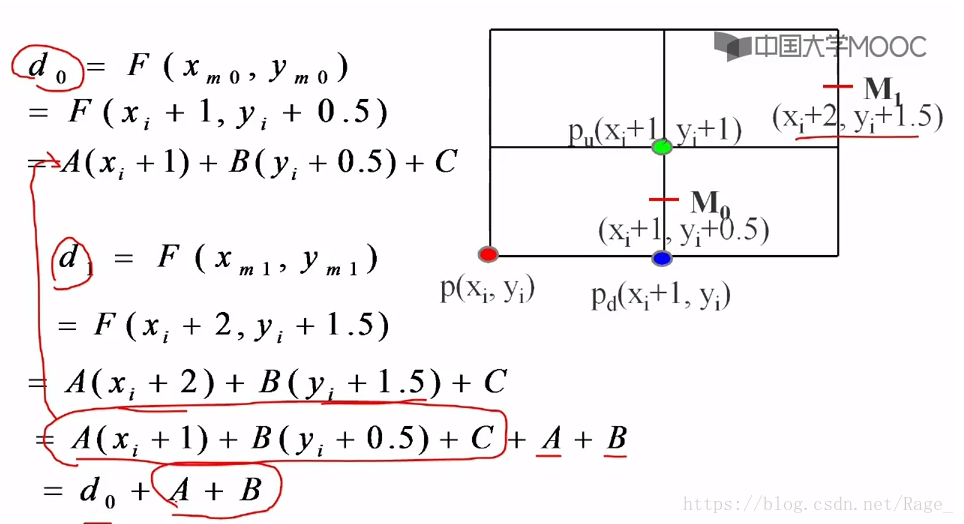
在d小于0的情况下:
上面已经推导的很清晰:稍微解释一下,求解d0是把M0代进去,求第二个点,d1是把M1代进去,求紧接着的下一个点。
最终推导出di = di-1 + A +B,增量为A+B
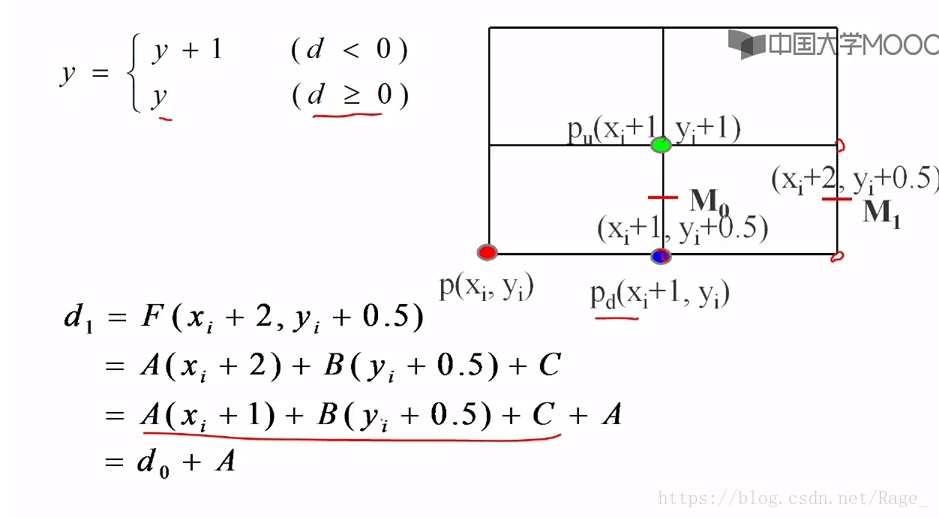
在d大于等于0的情况下:
这个也一样,最终推导出di+1=di+A,增量为A。
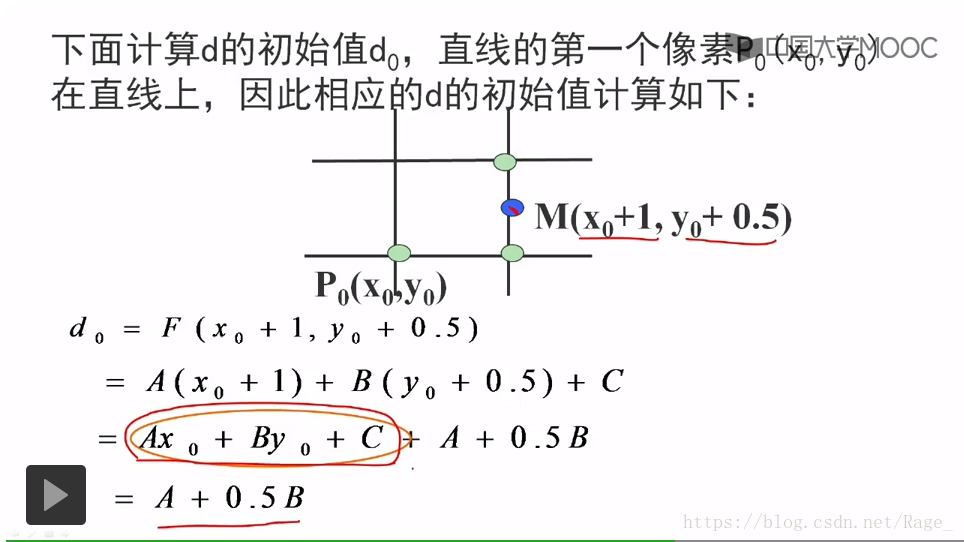
还缺少关键一部,那就是计算d的初始值d0的值:
P0为起始点,是直线上的点。所以下一个点的中点M必定为(x0+1,y+0.5),将M带入到直线方程中,得到如上的公式,由于x0,y0是直线上的点,满足方程等于0.所以Ax0+By0+C等于0.
所以d0 = A+0.5B!
最终的方程也就出来了,
但是由于(x0, y0)在直线上,所以F(x0, y0) = 0,因此,d的初始值为a + 0.5b。
d的初始值包含小数,因此可以用2d来代替d,写出仅包含整数运算的算法:
Bresenham算法
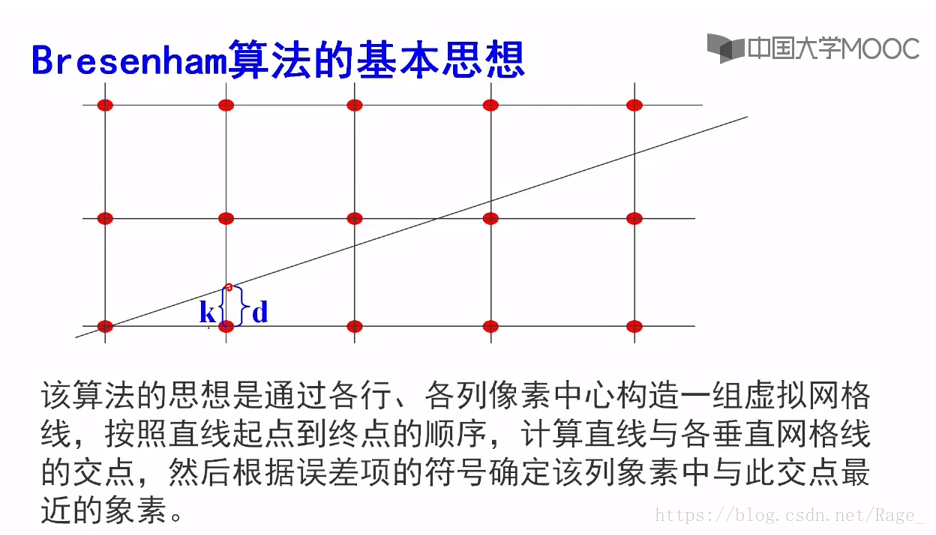
Bresenham算法也是一种计算机图形学中常见的绘制直线的算法,其本质思想也是步进的思想,但由于避免了浮点运算,相当于DDA算法的一种改进算法。
我们看下基本思想:
其实就是看d的符号(值)来缺点y的值!k是斜率。
如上图来看:
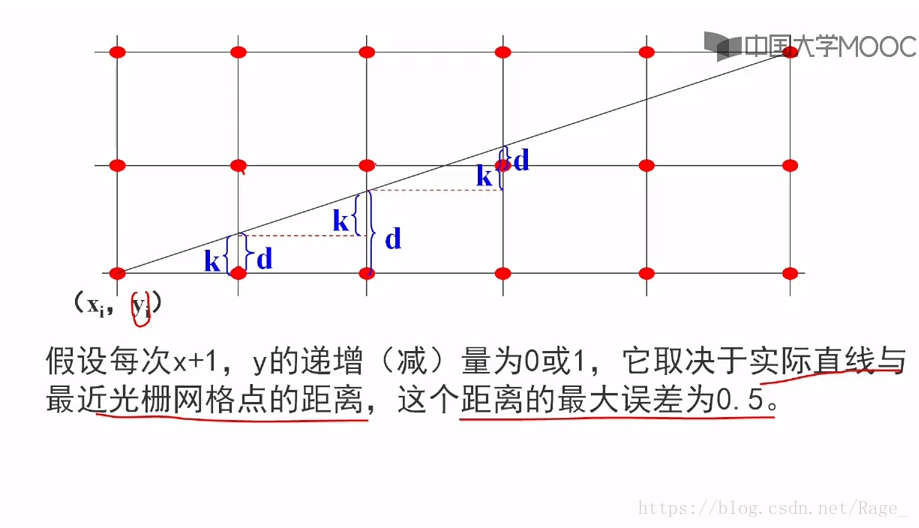
首先求d0=0。d=d+k。一旦d>=1,就减去1,保证d的相对性。就是上图的第三个d,是通过减1得到的。保证d在0到1之间!
判断如下:
此时y的下一个值,看d的值,如上图。但是上面也说到了,此时有浮点运算,如何提高到整数加法呢!我们发现其实只要看d的符号就可以,没必要算出d。所以另e=d-0.5。用e来代替d。
此时:
原来d0=0,所以此时e0等于0.5。下一个e=e+k。当e大于0,e也要减去1,保证e也在0到1之间。
改进二:
因为k=dy/dx,该算法会用到小数和除法,为了利于硬件实现,可以改用整数以避免除法,算法中只用到误差项的符号。所以
可以作如下替换:e' = 2 * e * dx;
最终结果出来了:
下一盘将附上代码