【Computer Graphics】3D引擎中的几何学：三维空间中的平面及相关计算

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/LeeXxs/article/details/82871804

内容

1. 参数化表达式
2. 求平面法向量
3. 求点到平面的距离
4. 求直线与平面交点
5. 求三个平面斜交

---

1.  参数化表达式

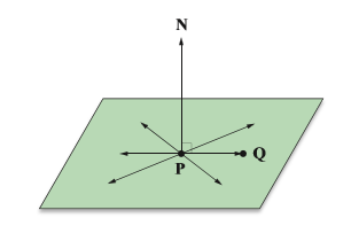
已知一个三维点 P 与法向量 N，设过点 P 且与 N 垂直的平面为点 Q 的合集，那么 Q 满足：

 

除此之外，平面方程还有一种常用的表达方式：

 

这里的 A，B，C 其实就是法向量 N 的 x，y，z 分量，而

---

2. 求平面法向量

• 已知平面上两条不共线的直线 ，，求法向量：

而根据叉积的定义，两个向量的叉积所得的向量和这两个向量垂直；

根据平面性质，垂直于平面的直线与平面上任何一条直线垂直；

因此，平面上两不共线直线的叉积(两平行直线的叉积为0)，就是该平面的法向量，方向遵循右手定则。 

• 已知平面方程 ，求法向量：

上述平面方程的三个系数所组成的向量 ，就是平面的一个法向量，证明如下：

设过平面上一点  的一个法向量为 ，该向量垂直于面上任意一条直线；

设  为平面上任意一点，则平面上的向量均可表示为：；

因为向量  与向量  垂直，所以其数量积为0，即：

整理得：

---

3. 求点到平面的距离

对于平面S1，有方程 ；

之前已经提到了 ，N为平面的法向量，P是平面S1上一点；

因为N是向量，P是一个点，可以先把  看做是向量N和向量OP的乘积(O为原点)，

以下描述和公式中的向量P皆指代向量OP。

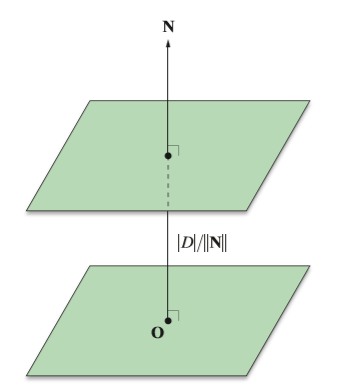
设过原点O与S1平行的平面为S0，因为：

其中为量N和向量P的夹角， 是向量P在法线向量N上投影的矢量大小，也是S0和S1的之间的距离，则：

S0和S1的之间的距离为：  。

同理，设任意一点R，假设过点R且与平面S1，S0平行的平面为S2，则S0和S2之间的距离d2为：

若平面法向量N为单位向量，则点R到平面S1的距离为S0和S1之间的距离减去S0和S2之间的距离，即：

若d=0，则点R位于平面上；

若d>0，则点R位于平面法向量所指的一侧，称为平面的正向侧

若d<0，则点R位于平面的负向侧

---

4. 求直线与平面交点

求一条直线和一个平面的交点是3D图形引擎中的普通计算，比如说在多边形裁剪中被广泛使用。

设过点S且与方向V平行的直线的表达式为：

设有一法向量为N且到原点的符号距离为D的平面，那么则存在：

即存在P(t)直线过该平面的一点(当然也可能直线和平面平行了，没有交点)

解上述关于P(t)的方程，即可获得直线与平面的交点。将P(t)替换为，可得：

求解关于t的方程，可得：

将t的值代入直程即可求得交点。

如果 ，则直线与平面平行，且平面法向量N与直线方向向量V垂直，

此时，若，则直线位于平面上，否则无交点。

---

5. 求三个平面斜交

一个空间的区域通常表示成由一系列平面为边界组成的凸面多面体的形式。该多面体的边和顶点可以通过执行多次三个平面的求交运算得出。

• 求三个平面交于一点

设 ，，，为任意三个平面；

通过计算以下方程组的解可以得到同时位于这三个平面的点Q：

          
          

写成矩阵形式：

其中，矩阵M的表达式如下：

假设矩阵M可逆，计算下式可得到三个平面的唯一交点Q：

如果矩阵M是奇异矩阵，即行列式为0：，则这三个平面不相交与一点；

当三个平面法向量位于同一平面时，会出现这种情况，下图所示就是情况之一：

• 求两个平面交于一条直线

设有两个不平行的平面 和 相交时，其交于一条直线，如下图所示：

交线的方向V与两个平面的法向量都垂直，可表示为 ；

已知交线的方向，为了完整获取表达式，还需要知道直线上的一点；

为此，构造经过原点且法向量为V的第三个平面 ，

可以确保三个平面交于一点，该点为平面  和  上的一点；

利用之前推倒的求三个平面的唯一交点的公式，可以得到交点Q：

则平面 和 交线的表达式为 。

---