【Computer Graphics】3D引擎中的几何学：三维空间中的直线及相关计算

内容

参数化表达式
求点到直线的距离
求直线间的距离

1. 参数化表达式

直线

假设3D空间中有两点 P1 和 P2，通过该两点所在的直线的参数化表达式为：

$\small P(t)=P1+ t*(P2-P1)=(1-t)*P1+t*P2$

可以理解为，过P1和P2两点的直线上的点，都是从P1点出发，沿着P2-P1的矢量方向可以找到的；

这里，t可以是任意实数，若t为0到1之间，则表示的是连接 P1 和 P2 的线段，即P(t)点位于两点之间。

射线

假设射线的端点为 S，且沿着某一方向 V 无限延伸，射线的参数化表达式为：

$\small P(t)=S+t*V$

这里，t 是大于等于 0 的实数；

该式也可以用来表示直线，如果令 $\small \small \mathrm{S = P1}$ ， $\small \small \mathrm{V = P2 - P1}$ ，该式与直线方程相同。

2. 求点到直线的距离

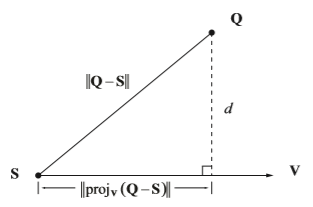
如图所示，已知由端点S和方向V定义的直线，和一点P，求点P到直线的距离d：

根据勾股定理可知：

$\small d^{2} =(Q-S)^{2} - [ proj_v(Q-S)]^{2}$

$\small d^{2} =(Q-S)^{2} - [\frac{(Q-S)\cdot V}{\left \| V \right \|^{2}}\cdot V]^{2}$

即点Q到直线的距离，等于Q-S的平方减去Q-S在方向V上的投影的平方；

对上式简化可得：

$\small \mathbf{ }d=$$\sqrt[]{(Q-S) - [\frac{(Q-S)\cdot V}{\left \| V \right \|^{2}}\cdot V]^{2} }$$$

3. 求直线间的距离

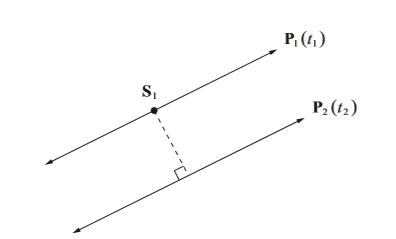
在二维空间中，两条直线，要么平行，要么相交于一点。在三维空间中，还存在一种情况，即两条直线既不相交也不平行，我们称之为扭曲。下面将通过简单计算，获取两条相扭曲的直线上两点之间的最近距离。

如上图所示，假设有两条直线，其参数化方程分别为：

$\small P_1(t_1) = S_1+t_1\ast V_1$

$\small P_2(t_2) = S_2+t_2\ast V_2$

那么求两条直线上两点之间的最近距离，就是求 $\small \left \| P_1(t_1)-P_2(t_2) \right \|$ 的最小值，设：

$\small f(t_1,t_2) = \left \| P_1(t_1)-P_2(t_2) \right \|^{2}$

展开平方，并且将 $\small P_1(t_1)$ 和 $\small P_2(t_2)$ 的表达式带入方程，暴力求解，得到：

$\small f(t_1,t_2) = S_1^{2}+t_1^{2}V_1^{2}+2 t_1 S_1\cdot V_1+S_2^{2}+t_2^{2}V_2^{2}+2 t_2 S_2\cdot V_2- 2(S_1\cdot S_2+t_1V_1\cdot S_2+t_2V_2\cdot S_1+t_1t_2V_1\cdot V_2)$

式子还挺长，不过可以通过分别令 $\small f$ 相对 $\small t_1$ 和 $\small t_2$ 的偏导数为0求解得到最小值：

$\small \frac{\partial f}{\partial t_1} = 2t_1V_1^{2}+2S_1\cdot V_1-2V_1\cdot S_2-2t_2V_1\cdot V_2 = 0$

$\small \frac{\partial f}{\partial t_2} = 2t_2V_2^{2}+2S_2\cdot V_2-2V_2\cdot S_1-2t_1V_1\cdot V_2 = 0$

消去2，上述两个等式整理后，可写成矩阵形式：

$\small \begin{bmatrix} V_1^{2} & -V_1\cdot V_2\\V_1\cdot V_2 & -V_2^{2} \end{bmatrix}\begin{bmatrix} t_1\\t_2 \end{bmatrix} = \begin{bmatrix} (S_2-S_1)\cdot V_1\\ (S_2-S_1)\cdot V_2 \end{bmatrix}$

解关于 $\small t_1$ 和 $\small t_2$ 的方程得：

$\small \frac{\partial f}{\partial t_1} = 2t_1V_1^{2}+2S_1\cdot V_1-2V_1\cdot S_2-2t_2V_1\cdot V_2 = 0$

$\small = \frac{1}{(V_1\cdot V_2)^{2}-V_1^{2}V_2^{2}} \begin{bmatrix} -V_2^{2} & V_1\cdot V_2\\-V_1\cdot V_2 & V_1^{2} \end{bmatrix} \begin{bmatrix} (S_2-S_1)\cdot V_1\\ (S_2-S_1)\cdot V_2 \end{bmatrix}$

根据上式可以求得 $\small t_1$ 和 $\small t_2$ 的值，代入函数 $\small f(t_1,t_2)$ 可以求得两条直线之间的最短距离的平方，再开方。或者代入两条直线的参数化方程，求得两条直线上距离最近的两个点，再求两点间的距离；

如果方向向量 $\small V_1$ 和 $\small V_2$ 是单位向量，则 $\small V_1^{2} = V_2^{2} = 1$ ，能进一步简化式子；

如果 $\small (V_1\cdot V_2)^{2}-V_1^{2}V_2^{2}$ 的值等于0，说明方程无解，则两条直线平行。此时两条直线间的距离等于一条直线上任意一点到另一条直线的距离；

如下图所示，点 $\small S_1$ 到直线 $\small P_2(t_2)$ 的距离，就是两条直线间的距离。