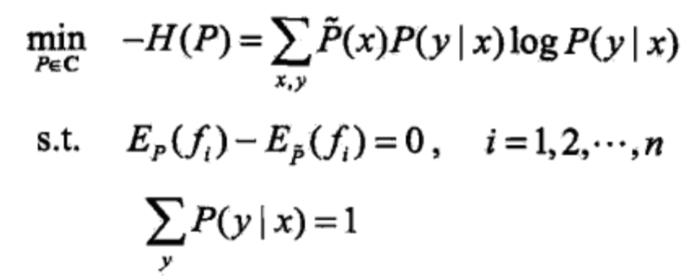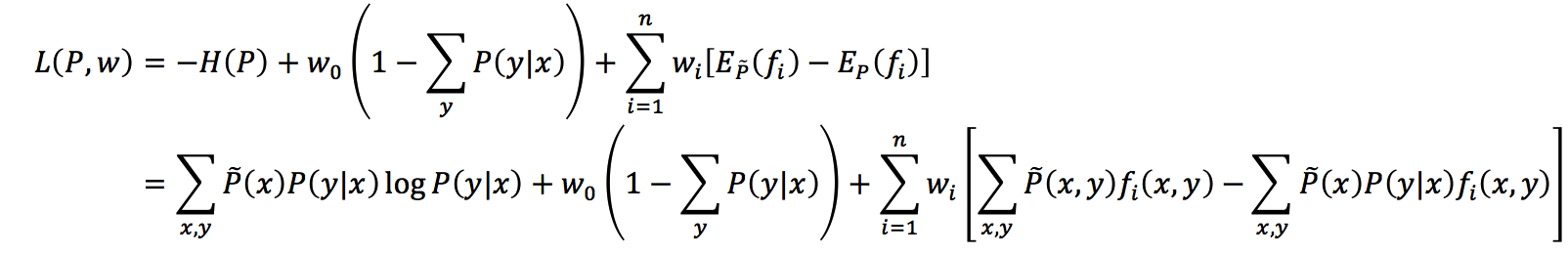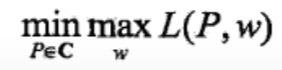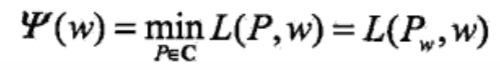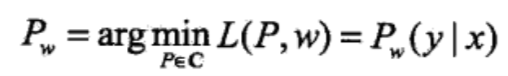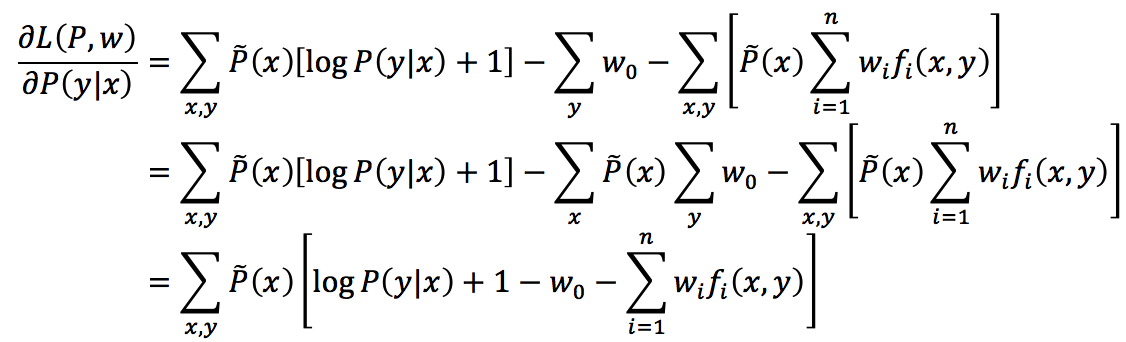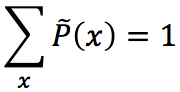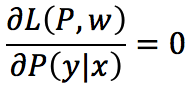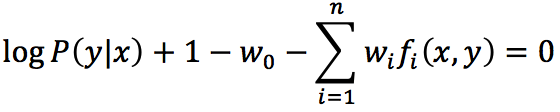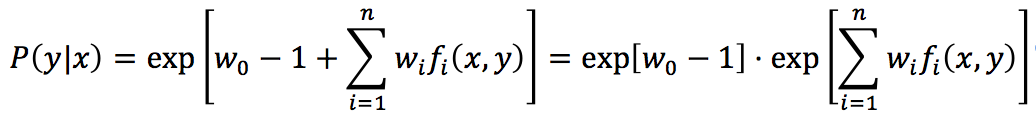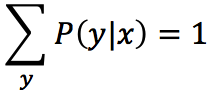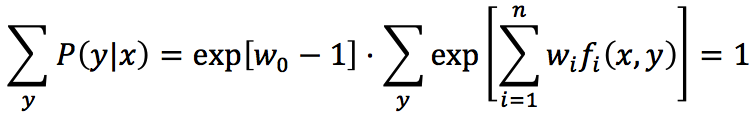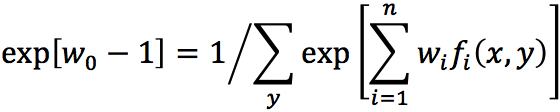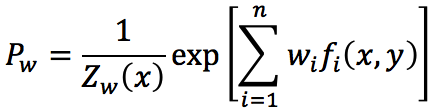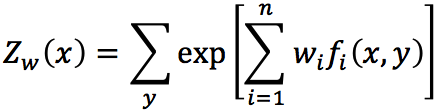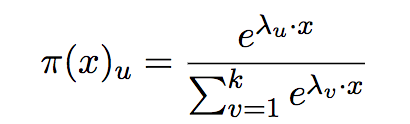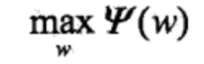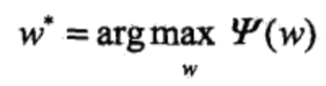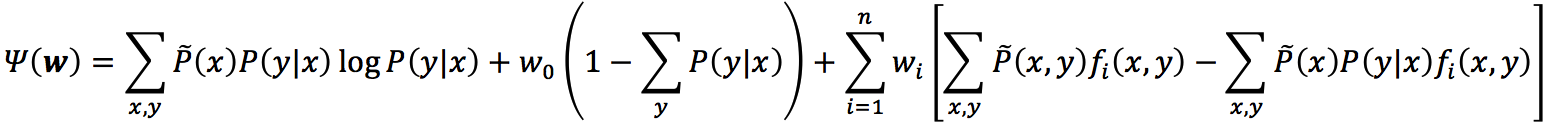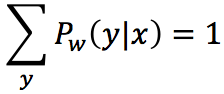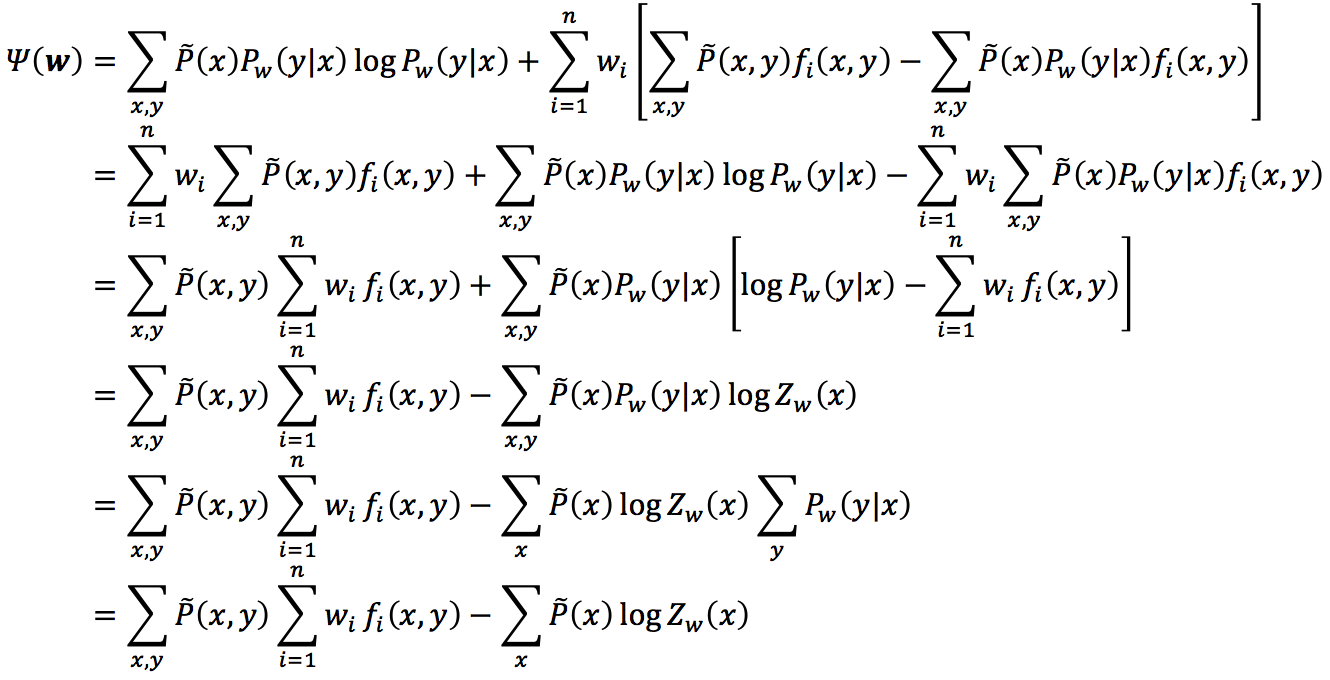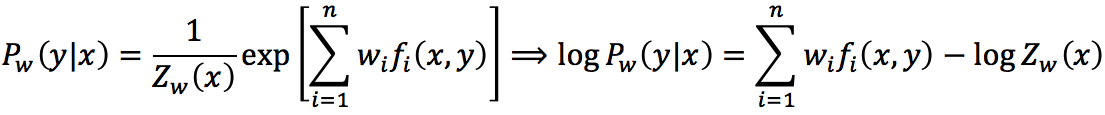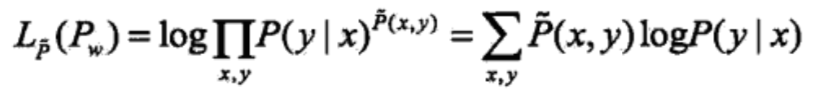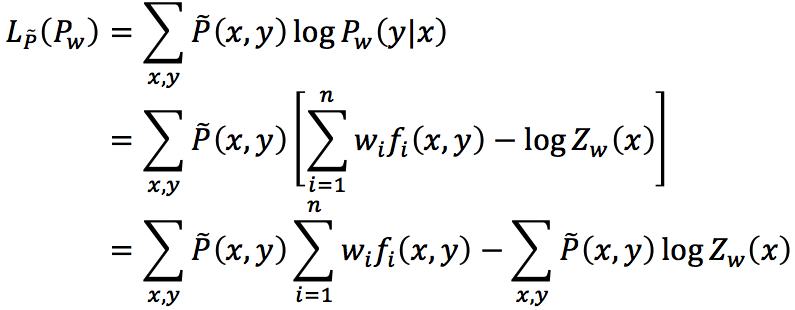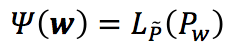最大熵模型（MaxEnt）：万法归宗（上）

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/baimafujinji/article/details/78992878

在上一篇文章【1】中，我们已经得到了与最大熵模型之学习等价的带约束的最优化问题：

注意上述公式中还隐含一个不等式约束即 P(y|x)≥0。求解这个带约束的最优化问题，所得之解即为最大熵模型学习的解。本文就来完成这个推导。

现在这里需要使用拉格朗日乘数法，并将带约束的最优化之原始问题转换为无约束的最优化之对偶问题，并通过求解对偶问题来求解原始问题。首先，引入拉格朗日乘子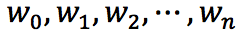，并定义拉格朗日函数L(P, w)：

According to [7], to find the solution to the optimization problem, we appealed to the Kuhn-Tucker theorem, which states that we can (1) first solve L(P, w) for P to get a parametric form for P* in terms of w; (2) then plug P* back in to L(P, w), this time solving for w*.

原始问题与对偶问题

最优化的原始问题是

通过交换极大和极小的位置，可以得到如下这个对偶问题

由于拉格朗日函数L(P,w)是P的凸函数，原始问题与对偶问题的解是等价的。这样便可以通过求解对偶问题来求解原始问题。

对偶问题内层的极小问题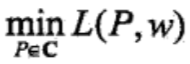 是关于参数w的函数，将其记为

同时将其解记为

接下来，根据费马定理，求L(P,w)对P(y|x)的偏导数

注意上述推导中运用了下面这个事实

进一步地，令

又因为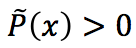，于是有

进而有

又因为

所以可得

即

将上面的式子带回前面P(y|x)的表达式，则得到

其中，

Z_w(x)称为规范化因子； f _i(x,y)是特征函数；w_i是特征的权值。由上述两式所表示的模型P_w=P_w(y|x)就是最大熵模型。这里，w是最大熵模型中的参数向量。注意到，我们之前曾经提过，特征函数可以是任意实值函数，如果f_i(x,y)=x_i，那么这其实也就是【5】中所说的多元逻辑回归模型，即

此亦是万法归宗的第一层境界。关于上面这个式子的一个简单例子，你还可参考文献【6】。

极大似然估计

下面，需要求解对偶问题中外部的极大化问题

将其解记为w*，即

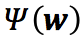
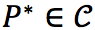
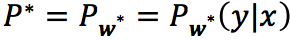
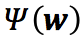
这就是说，可以应用最优化算法求对偶函数的极大化，得到w*，用来表示。这里，是学习到的最优模型（最大熵模型）。于是，最大熵模型的学习算法现在就归结为对偶函数的极大化问题上来。

前面我们已经给出了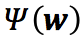的表达式：

由于，其中

于是将P_w(y|x)带入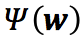，可得

注意其中倒数第4行至倒数第3行运用了下面这个推导：

下面我们来证明对偶函数的极大化等价于最大熵模型的极大似然估计。已知训练数据的经验概率分布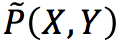，条件概率分布P(Y|X)的对数似然函数表示为

当条件概率分布P(y|x)是最大熵模型时时，对数似然函数为

对比之后，不难发现

既然对偶函数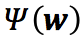等价于对数似然函数，于是也就证明了最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计这一事实。此亦是万法归宗的第二层境界。由此，最大熵模型的学习问题就转换为具体求解“对数似然函数极大化的问题”或者“对偶函数极大化的问题”。

参考文献与推荐阅读材料

【1】最大熵模型（MaxEnt）：万法归宗（上）

【2】李航，统计学习方法，清华大学出版社

【3】https://www.cnblogs.com/wxquare/p/5858008.html

【4】http://blog.csdn.net/itplus/article/details/26550273

【5】http://blog.csdn.net/baimafujinji/article/details/51703322

【6】https://www.youtube.com/watch?v=hSXFuypLukA&list=PLJV_el3uVTsPy9oCRY30oBPNLCo89yu49&index=10

【7】http://www.cs.cmu.edu/afs/cs/user/aberger/www/html/tutorial/node9.html

（本文完）