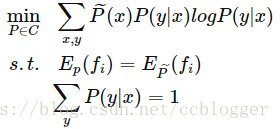最大熵模型学习过程

前言
在将最大熵模型之前,先学习一下准备知识。
①拉格朗日乘子法

②贝叶斯定理
- Bayes定理用来描述两个条件概率之间的关系。若计P(A)和P(B)分别表示事件A和事件B发生的概率,P(A|B)表示事件B发生的情况下事件A发生的概率,P(A,B)表示事件A和B同时发生的概率,则有:

结合1,1,1,2可以得出贝叶斯公式:

③熵
熵是用来表示随机变量不确定性的度量。

H(x)依赖于X的分布,而与X的具体值无关。所以我们经常用H(P)来表示H(X), H(X)越大,表示X的不确定性越大.
④条件熵

⑤似然函数和最大似然函数
似然性与概率意思相近,但还是有区别,概率是在已知一些参数的情况下,来预测观察所得到的结果;似然性是在已知一些观察得到的结果的情况下,对一些事物的未知参数进行估计
例如
1.1 似然是知道事件结果推参数。举个栗子:如历史上,美国数学家Feller为了得知抛硬币正反的概率参数,一口气抛了10000次硬币,得到结果是4972次正面和5021次反面(事件结果),由此可得到一个硬币正反的概率参数的简单结果:正面概率约0.497,反面约为0.502。
.1.2 概率是知道参数推事件结果。举个栗子:小明知道了Feller大神的实验结果(概率参数),想要算一下抛硬币连续两次正再连续两次反面额概率,那么就是0.497*0.497*0.502*0.502 概率约为0.062(事件结果)。
最大似然函数:选取似然函数(一般是概率密度函数),整理之后求取最大值

注意:实际应用中是对似然函数求对数(即称为对数似然函数),然后再对对数似然函数求取最大值;因为对数有严格单调性,这样对数求得的最大值与实际最大值结果是相同的。
一.什么是最大熵原理
MaxEnt (最大熵模型)是概率模型学习中一个准则,其思想为:在学习概率模型时,所有可能的模型中熵最大的模型是最好的模型;若概率模型需要满足一些约束,则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。最大熵原理指出,对一个随机事件的概率分布进行预测时,预测应当满足全部已知的约束,而对未知的情况不要做任何主观假设。在这种情况下,概率分布最均匀,预测的风险最小,因此得到的概率分布的熵是最大

于是p(A)=P(B)=3/20
p(C)=P(D)=P(E)=7/30
二.最大熵模型的定义
经验分布
- 经验分布是指通过训练数据T上进行统计得到的分布。我们需要考察两个经验分布,分别是x,y的联合经验分布以及x的分布。其定义如下:

- (3.3)中count(x,y)表示(x,y)在数据T中出现的次数,count(x)表示x在数据T中出现的次数。
约束条件
- 对于任意的特征函数f,记 E p ! ( f ) 表示f在训练数据T上关于 p ! (x, y) 的数学
期望。 E p ( f ) 表示f在模型上关于p(x,y)的数学期望。按照期望的定义,有:

我们需要注意的是公式(3.5)中的p(x,y)是未知的。并且我们建模的目标是p(y|x),因此我们利用Bayes定理得到p(x,y)=p(x)p(y|x)。此时,p(x)也还是未知,我们可以使用经验分布对p(x)进行近似。
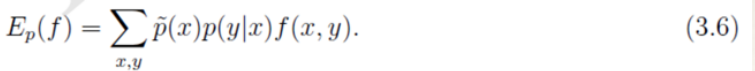
对于概率分布p(y|x),我们希望特征f的期望应该和从训练数据中得到的特征期望是一样的。因此,可以提出约束:
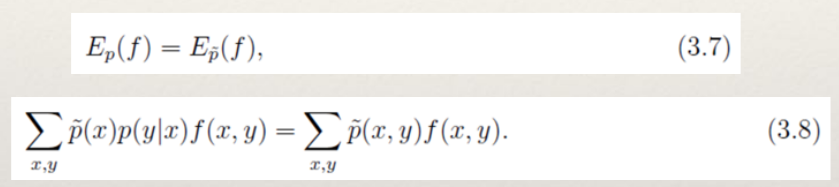
- 假设从训练数据中抽取了n个特征,相应的便有n个特征函数以及n个约束条件。
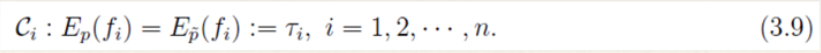

三.最大熵模型的学习

于是给出形式化的最大熵模型:

将求最大值改为求最小值
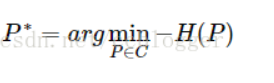
由于拉格朗日方法专门解决那些等式约束或不等式约束的目标函数最小值的问题
最大熵模型的求解思路和步骤如下:



注意:下面的就是参数w


在得到内层极小问题的解p的解后,代入到
(
)中,接着求外层关于
的等式的极大值问题


接下来求最大值点就行了
当然也可以用条件概率分布P(y/x)的对数似然函数来表示对偶函数的极大化(4.10)的式子,这样就求解对偶函数极大化就简单多了
下面证明对偶函数的极大化等价于最大熵模型的对数似然函数:

四.最大熵模型的实例
- 题:假设随机变量X有5个取值{A,B,C,D,E},且满足条件P(A)+P(B)=0.3且P(A)+P(B)+P(C)+P(D)+P(E)=1。求最大熵模型。
- 为了方便,分别用y 1 ~y 5 表示A~E于是最大熵模型的最优化问题是:
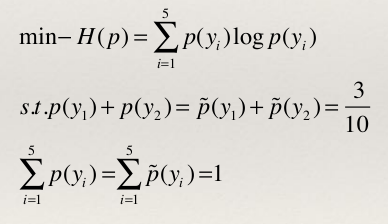
求解过程:第一步:引进拉格朗日乘子w0和w1,定义拉格朗日函数如下:
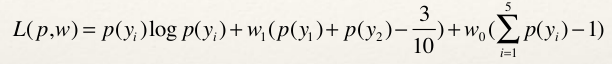
第二步:根据拉格朗日对偶性,可以通过求解对偶最优化问题得到原始最优化问题的解。所以求解max min L(p,w)首先需要求解关于p的极小化问题。为此需要固定w0和w1。求对p的偏导数:
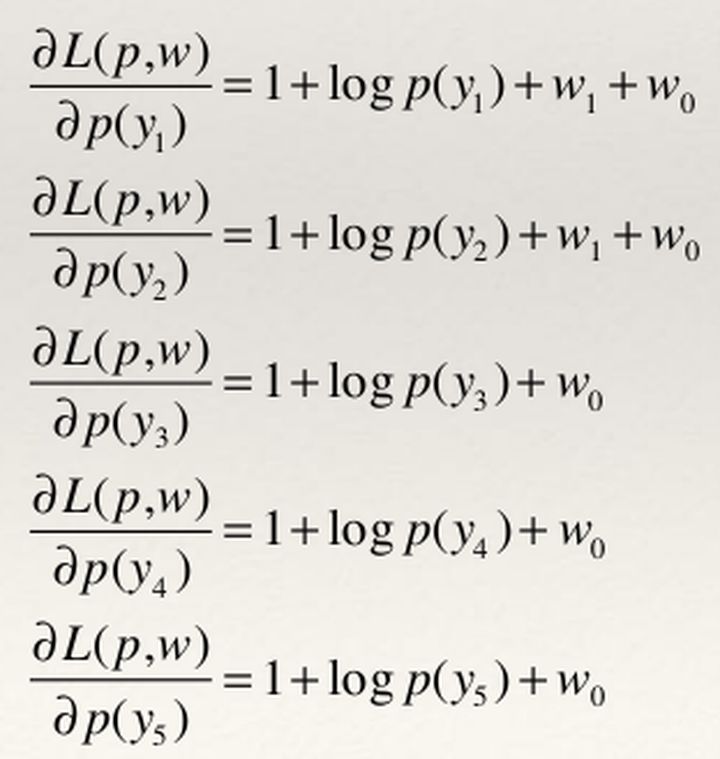
上式所有偏导等式都等于0,即可分别得出P(y1),p(y2),P(y3),P(y4),P(y5), 它们是关于w0和w1的关系式
然后将P(y1),p(y2),P(y3),P(y4),P(y5)代入L(p,w)中,得出关于w的式子
第三步:再求L(p,w)关于w的极大化问题
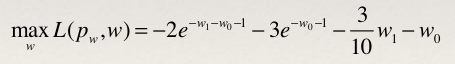
第四步:分别对w0和w1求偏导,并令其等于0,可以得到

五.最优化算法
公式Lp(p)式子中没有显式的解析解,因此需要借助于其他的方法。由于目标函数是一个 凸函数,所以可以借助多种优化方法来进行求解,并且能保证得到全局最优解。

①GIS算法

②IIS算法

最优化算法解析可以参考:https://blog.csdn.net/itplus/article/details/26550369
以及参考李航的《统计学习方法》104页
6.优缺点

7.应用场景
气候变化背景下基于最大熵模型(MaxEnt)预测黄连的适生区分布
https://www.hanspub.org/journal/PaperInformation.aspx?paperID=23007
气候变化情景下基于最大熵模型的青海云杉潜在分布格局模拟
http://www.ecologica.cn/stxb/ch/html/2019/14/stxb201809151999.htm