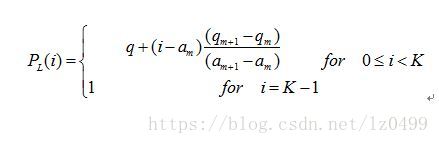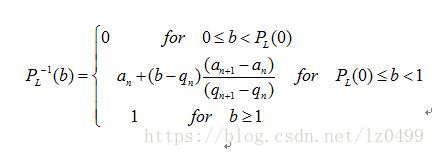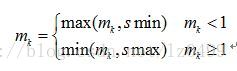一种控制分段映射直方图均衡化的图像对比度增强算法

1.Histogram Specification（直方图规格化）

1.1频率和概率

1.2直方图规则化的目的

1.Histogram Specification（直方图规格化）

全局直方图均衡化------概率分布函数每个灰度值的所对应的概率都相同，被广泛应用于图像处理领域中。但是现实比较好的图像绝对不会呈现直方图均衡化之后的那种概率分布。许多真实的图像中，像素值的分布也可能接近是线性分布。直方图均衡化之后的图像，虽然对比度会比原始图像高很多，但是看起来很不自然。

直方图规格化是一种更加普遍的技术：通过改变原始图像灰度值的分布情况，使得其能够匹配任意像素灰度值分布。这种技术在某些应用领域具有较好的使用价值：一系列在不同曝光下或不同光照环境下，亦或者是不同相机所拍摄的图像，我们想让这些图像在打印或显示器显示的时候看起来具有相类似的效果（当然只是对比度或亮度方面而言）时，就可以使用直方图规格化这种技术。类似于直方图均衡化，直方图规格化也是以累积直方图信息为依据进行相应的处理。

1.1频率和概率

直方图中的纵坐标描述的是图像中相对应的像素灰度值所出现的频率。也就是说直方图是图像灰度值的频率分布。对于一幅大小为 $M\times N$ 的图像 $I$ ，直方图中所有bin $h(i)$ 相加之和必定等于整幅图像的像素总和。即：

$\sum_{i=0}^{K-1}h(i)=M\times N$

对应的归一化直方图为：

$p(i)=\frac{h(i)}{M*N} 0\leqslant i< K$

归一化的直方图又称为图像灰度值的概率分布或概率密度函数（pdf）， $p(i)$ 是图像灰度值 $i$ 所对应的概率。任何累积概率密度函数的值都为1，其对应的概率密度函数必定满足如下关系：

$\sum_{i=0}^{K-1}p(i)=1$

相应的累积直方图称所对应的概率密度函数我们称之为累积分布函数（CDF）。

$p(i)=\frac{H(i)}{H(K-1)}=\frac{H(i)}{MN}=\sum_{j=0}^{i}\frac{h(j)}{MN}=\sum_{j=0}^{i}p(j) 0\leq i< K$

累积概率分布函数我们可以按照如下算法计算：

1.2直方图规则化的目的

图像规则话的目的是通过图像的点操作改变图像 $I_{A}$ ，使得其概率分布函数与给定的图像的概率分布函数尽可能的相近。因此，我们可以得到一个映射函数：

$a^{'}=f_{hs}(a)$

使用图像的点操作，通过映射函数使得原始图像的每一个像素点变为 ${a}'$ 。即

$P_{A}\approx P_{B} \, 0\leqslant i< K$

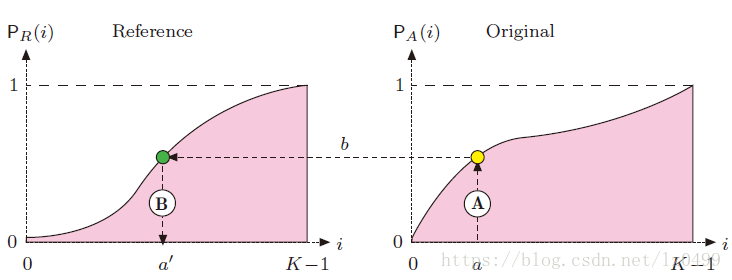
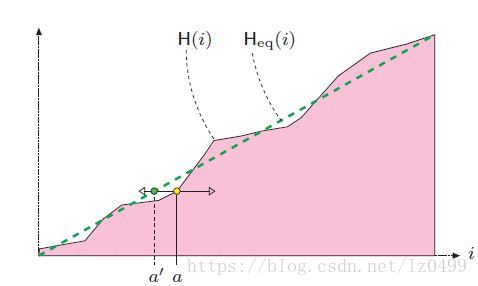
如下如所示：

上图中：给定一幅参考图像，其对应的累积概率分布函数为 $P_{B}$ ，原始图像的累积概率分布函数为 $P_{A}$ ，通过图像的点操作使得映射函数 $f_{hs}$ 的结果为： $a\rightarrow {a}'$ ，把原始图像中的每一点 $a$ 替换为 ${a}'$ 所得到最终的累积直方图就与参考累计直方图很接近。这个过程主要有两步：

对原始图像中的每一个像素，从原始图像的累积概率分布函数中可得： $b=P_{A}(a)$
对于每一个b，从左侧的累积概率分布函数的反函数得到： ${a}'=P_{B}^{-1}(b)$

$f_{hs}={a}'=P_{B}^{-1}(P_{A}(a))\, 0\leq a< K\, 0\leqslant b\leqslant 1\, \, \, (1)$

1.3分段线性分布

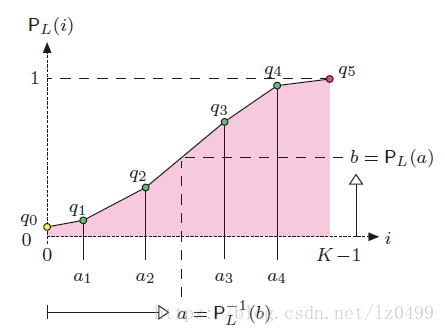
如果给定的参考分布 $P_{R}$ 是一个连续可求反函数的分布，那么映射函数我们可以通过上述的公司很容易的求得。实际上我们也可以把参考分布函数用一些列点分隔开来，用分段函数表示原来的概率分布函数。假设分段的概率分布函数为 $P_{L}$ ，对应的分段间隔点为：

$L=\left [ \left \langle a_{0},q_{0} \right \rangle ,\left \langle a_{1},q_{1} \right \rangle,\cdots ,\left \langle a_{k},q_{k} \right \rangle,\cdots \left \langle a_{N},q_{N} \right \rangle\right ]$

任意一个图像的灰度值 $a_{k}$ 以及累积概率分布函数所对应的函数值 $q_{k}$ （ $0\leqslant a_{k}< K\, \, \, 0\leq q_{k}< 1$ ），两个端点为 $\left \langle a_{0},q_{0} \right \rangle$ 和 $\left \langle a_{N},q_{N} \right \rangle$ 被固定在 $\left \langle 0,q_{0} \right \rangle$ 和 $\left \langle K-1,1 \right \rangle$ 。如果一个函数有反函数，那么这个函数必定是单调的，即 $q_{k}< q_{k-1}\, \: 0\leq k< N$ 。如上如所示，即为一个可求反函数的概率分布函数。

分段的概率分布函数为 $P_{L}$ 可以通过线性插值的方式获得控制点之间的对应的函数值。即：

通过（1）式，我们需要求得分布函数的反函数 $P_{L}^{-1}$ ，如上如所示，我们知道 $P_{L}(i)$ 在 $b<P_{L}(0)$ 的时候不和求反函数。我们可以使得 $b<P_{L}(0)$ 的时候都设置为0，则可以得到近似的可求反函数的分布函数。因此，我们可以通过如下式子求得反函数的函数值为：

1.4传统的图像均衡化

传统的图像均衡化通过如下公式实现。

$f_{eq}=\left \lfloor H(a)\cdot \frac{K-1}{MN} \right \rfloor$

其中，MN分别为图像的长和宽，[0,K-1]为图像的灰度值范围，H()为图像的累积直方图。

通过直方图均衡化，可以使得图像的的灰度值尽量的均匀分布，使得图像的对比度增强。

如下如图所示：

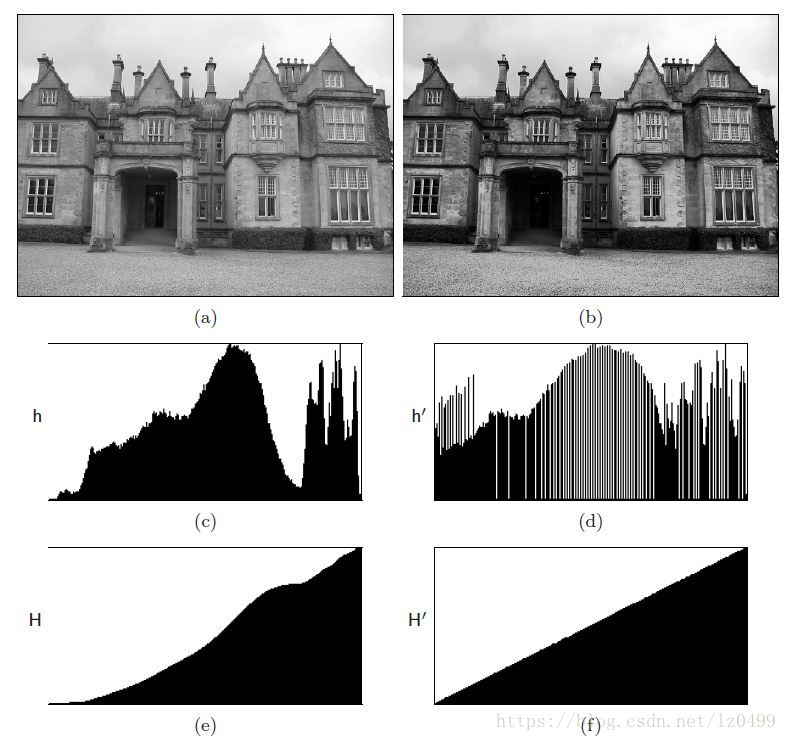
具体图像实例如下所示：

左侧图像分别为原始图、原始图的直方图、原始图的累积直方图

右侧图像分别为均衡化之后的图、均衡化后的直方图、均衡化后的累积直方图

传统的直方图均衡化会把较暗图像的噪声放大，并使得最后的图像不是很自然。论文《Color and Contrast Enhancement by Controlled Piecewise Affine Histogram Equalization》所提出的方法是对传统直方图均衡化的优化。把原始累积直方图进行分段处理，并使得分段后的累计直方图基本上呈线性变化，通过局部信息控制对比度变化的斜率抑制噪声。通过控制分段累积直方图的斜率以使图像在不同亮度区域分别进行直方图均衡化。

2.算法实现思路

令 $u(i,j),\, \, \, i=0,1,2\cdots n_{x}-1\, \, \, j=0,1,2\cdots ,n_{y}-1$ 是范围为[0.255]的图像灰度值，令F:[0,255]->[0,1]为图像的累积概率分布函数，即：

$F(x)=\frac{\left | (i,j):u(i,j)\leq x \right |}{D}$

其中D为图像的像素数量。

对于分割参数点数目N，我们考虑其在[0,255]的分割点为 $0\leqslant y_{0}< y_{1}< y_{2}\cdots < y_{N}=255$ ，其中 $y_{k}=255k/N,\, \, k=0,1,2\cdots ,N$ 。我们定义新的分割点 $x=F^{-1}(\frac{y_{k}}{255}),\, \, k=0,1,2,\cdots ,N$ .

对于每一个新的分割段 $I_{k}=\left [ x_{k},x_{k+1} \right ]$ ，算法会构建一个线性变换 $T_{k}(x)$ ，使得 $\left [ x_{k},x_{k+1} \right ]$ 映射到 $\left [ y_{k},y_{k+1} \right ]$ 。即：

$T_{k}(x)=y_{k}+m_{k}(x-x_{k})\, \, \, k=0,1,2\cdots ,N-1$

对于上述线性变换的斜率为：

$m_{k}=\frac{y_{k+1}-y_{k}}{x_{k+1}-x_{k}}$

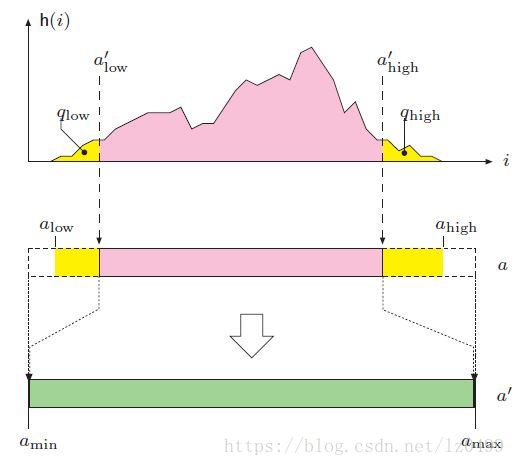
即如下图所示：

上述公式中的线性插值，相当于把区间 $\left [ x_{k},x_{k+1} \right ]$ 映射至 $\left [ y_{k},y_{k+1} \right ]$ 。

如果斜率太小，上述的线性映射函数会压缩直方图信息，有可能牺牲太多的对比对；如果斜率太大，可能会放大噪声，尤其是暗区域的噪声。为了避免上述缺陷，线性映射函数必须进行一定限制。我们使用了两个新的参数 $smin$ 和 $smax$ 来限制斜率的大小。即：

总结下：其实算法的总体思路是先在原始累计概率直方图中用N个点等分，并求得其等分点的累积概率函数反函数值。由于等分点的原因，累积概率分布函数的反函数值的因变量成比例，对应的自变量即为新的等分点x,然后再把新的等分点x映射到原始函数的等分点y。由于新的等分点区间像素数量相同，原始图像的因变量y区间也是相等的。即在累积直方图信息中，y区间的像素数量都是相同的，即类似直方图均衡化中的线性关系，相当于分段做了一个直方图均衡化。如下图所示：

左侧为累积概率分布函数的反函数。右侧为原始图像的累积概率分布函数。假设x1,x2,x3处的函数值分别为0.1,0.2,0.3，x1,x2,x3之间的像素数量都是相等的。现在从坐标原点开始，把x区间的像素值分别映射到原始图像的y区间。由于每一个x区间的像素数量都是相等的，映射到y区间的像素数量也是相等，又因为y区间的区间大小都是一样大，因此，最后在累积直方图中，每一分段区间中的横坐标的差值和纵坐标的差值必定是相等的，全局来看累积直方图就是近似线性的关系。在x区间插值到y区间的时候，我们可以通过控制其线性插值函数的斜率从而控制其区间内对比度的改变。如果区间斜率比较小，那么插值之后对比度灰比较小；但是当斜率比较大的时候，会相应的扩大暗区像素的灰度值，使得噪声可能比较明显。当分割点足够多的时候，其结果与图像直方图十分接近了。

其算法伪代码如下：

3.算法代码实现


void maxmin(Mat img_input,double *min,double *max)
{
	minMaxLoc(img_input,min,max,NULL,NULL);
}

void sort_data(Mat img_input,Mat F)
{
	
	cv::sort(F,F,CV_SORT_EVERY_ROW+CV_SORT_ASCENDING);

}


int inverse_cumulative_function(float Fu,Mat F)
{
	int pos;
	float *data = F.ptr<float>(0);

	if(Fu<0)
		return 0;

	pos = (int)ceil((double)Fu);
	pos = pos -1;

	return data[pos];
}



void affine_transformation(Mat img_input,Mat img_PEQ,float x0,float y0,float x1,float y1)
{
	float slope;
	int i,j,tmp;
	slope = (y1-y0)/(x1-x0);

	for(i = 0;i < img_input.rows;i++)
	{
		float *data = img_input.ptr<float>(i);
		float *out_data = img_PEQ.ptr<float>(i);
		for(j=0;j<img_input.cols;j++)
		{
			if(data[j]>=x0 && data[j]<=x1)
			{
				 tmp = (y0+slope*(data[j]-x0));
				 if(tmp > 255)
					 tmp = 255;
				 if(tmp < 0)
					 tmp = 0;
				 out_data[j] = tmp;
			}
		}
	}

}

void piecewise_transformation(Mat img_input,Mat img_PEQ,int N, float smin,float smax)
{
	float x0,x1,y0,y1,Fu,slope;
	double min,max;
	int k,col,row,dim;
	//Size size(1,img_input.cols*img_input.rows);
	//Mat F(size,CV_32FC1);
	Mat F;

	dim = img_input.cols*img_input.rows;
	img_input.reshape(0,1).copyTo(F);

	maxmin(img_input,&min,&max);
	sort_data(img_input,F);

	x0 = min;
	y0 = 0.0;
	
	
	for(k = 1;k <=N;k++)
	{
		Fu = (float)(dim*k)/(float)(N+1);//还需要考虑到原点。即原点+N个点把累积分布函数等分成N段
		y1 = (255.0*k)/(N+1);
		x1 = inverse_cumulative_function(Fu,F);//用排序的方式计算其累计分布函数的反函数值
		if (x1 > x0) 
		{
            slope = (y1 - y0) / (x1 - x0);//插值计算，相当于把分割点x映射到[y0,y1]的范围

            if (slope > smax)
                y1 = smax * (x1 - x0) + y0;

            if (slope < smin)
                y1 = smin * (x1 - x0) + y0;
		}

		affine_transformation(img_input,img_PEQ,x0,y0,x1,y1);
		x0 = x1;
        y0 = y1;

	}

	//如果反函数的分割点灰度值大小小于原始图像的最大值，那么还需要再做一次映射
	if (x0 < max) 
	{
        y1 = 255.0;
        x1 = max;
        slope = (y1 - y0) / (x1 - x0);

        if (slope > smax)
            y1 = smax * (x1 - x0) + y0;

        if (slope < smin)
            y1 = smin * (x1 - x0) + y0;
		affine_transformation(img_input,img_PEQ,x0,y0,x1,y1);
	}

}



int main()
 {
	Mat img=imread("car.png",IMREAD_GRAYSCALE);
	Mat img_PEQ(img.size(),CV_8UC1);
	Mat img_float(img.size(),CV_32FC1);
	Mat img_float_PEQ(img.size(),CV_32FC1);
	Mat equalize_hist;


	img.convertTo(img_float,CV_32FC1);
	
	float smin = 0,smax = 5;
	int N = 10;
	piecewise_transformation(img_float,img_float_PEQ,N,smin,smax);
	convertScaleAbs(img_float_PEQ,img_PEQ);
	cv::equalizeHist(img,equalize_hist);
	
	namedWindow("Original img",0);
	namedWindow("Modified img",0);
	namedWindow("equalize_hist img",0);

	

 
	imshow("Original img",img);
	imshow("Modified img",img_PEQ);
	imshow("equalize_hist img",equalize_hist);

	imwrite("lena_min0_max5.bmp",img_PEQ);
	imwrite("lena_equalize_hist.bmp",equalize_hist);
	
 // 等待6000 ms后窗口自动关闭
	
	waitKey(60000);
 }

4.算法效果

左侧为原始图，中间为全局均衡化图像，右侧为N=10，smin=0,smax=5对应的结果。右侧图在该参数下很接近全局直方图均衡化

左侧为原始图，中间为N=10，smin=0,smax=5对应的结果，右侧为直方图均衡化结果，该参数下对比度有所减小

左侧为直方图均衡化结果，中间为N=10，smin=0.5,smax=1的结果，右侧围原始图像。
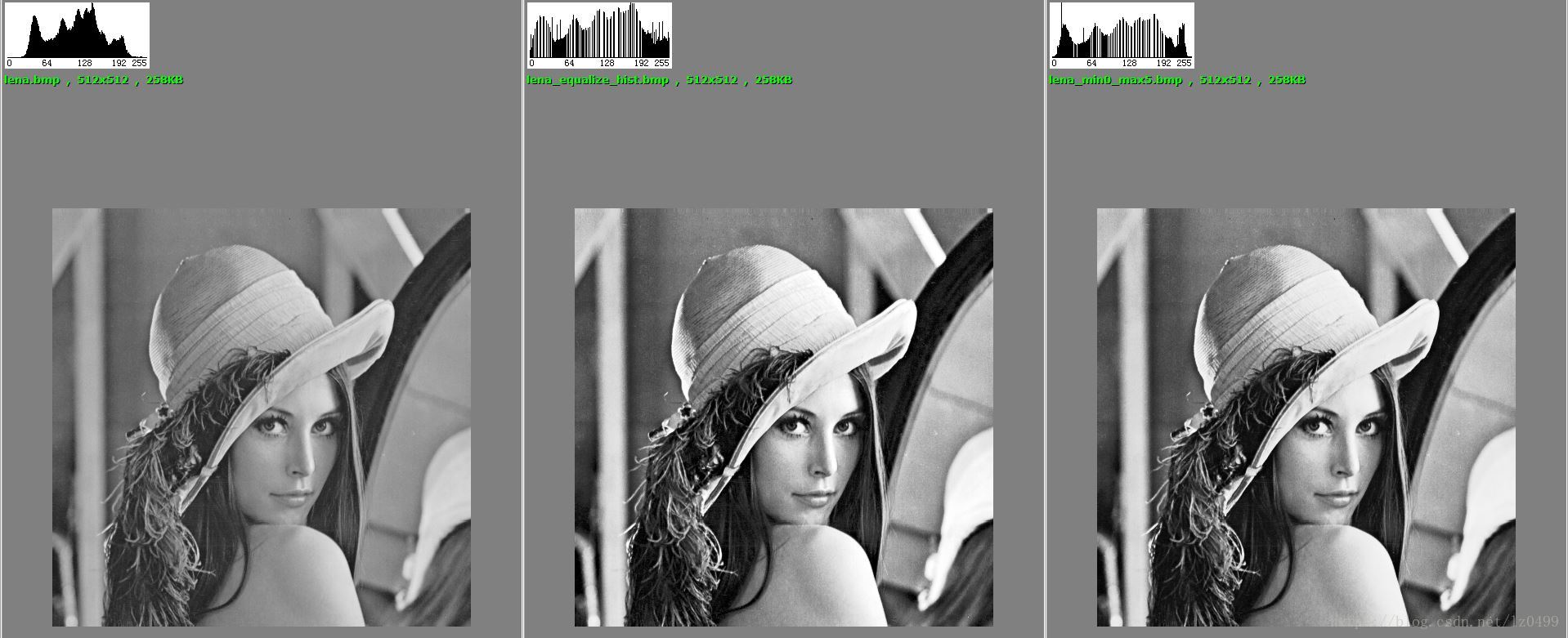
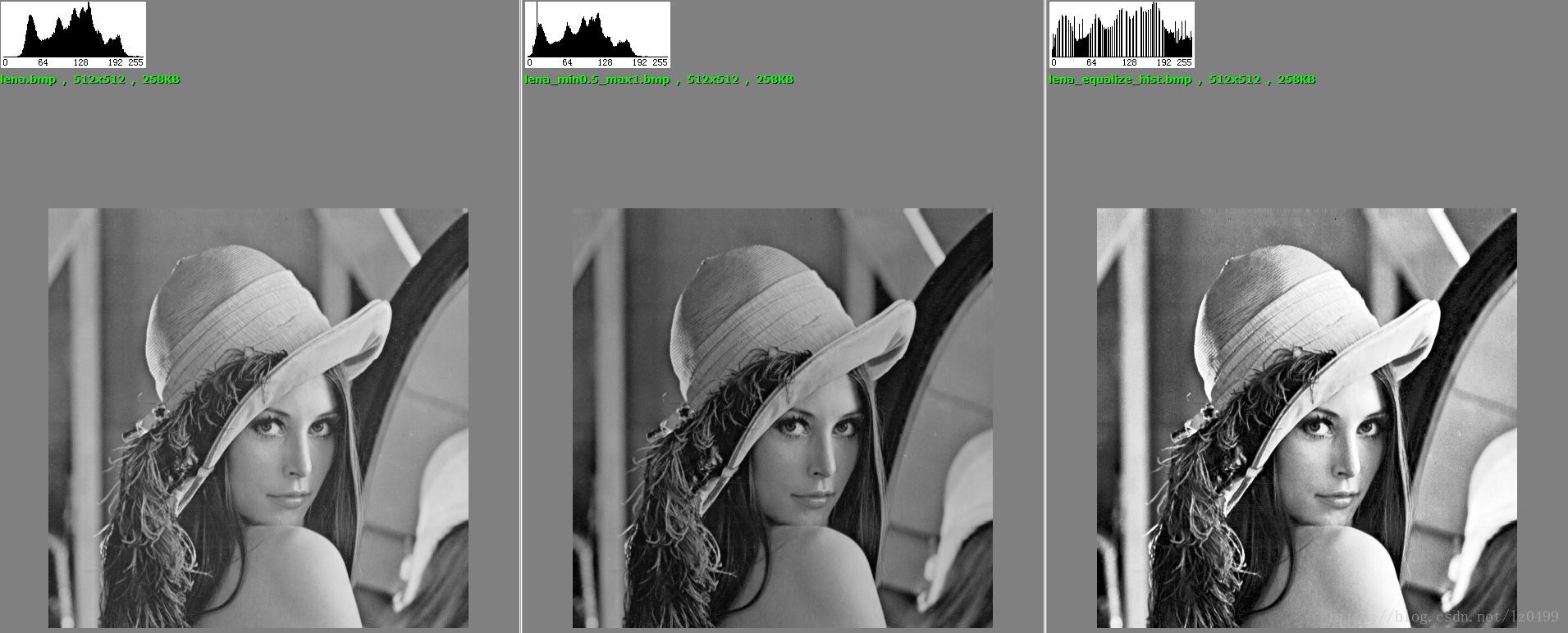
该参数下能够把暗区背景适当提亮，但是又能减小暗区噪声。

参考资料：

1.http://www.ipol.im/pub/art/2012/lps-pae/

2.《Principles of Digital Image Processing Fundamental Techniques》->https://download.csdn.net/download/lz0499/9954437

一种控制分段映射直方图均衡化图像对比度增强算法

一种控制分段映射直方图均衡化的图像对比度增强算法

1.Histogram Specification（直方图规格化）

1.1频率和概率

1.2直方图规则化的目的

1.3分段线性分布

1.4传统的图像均衡化

2.算法实现思路

3.算法代码实现

4.算法效果

猜你喜欢