HDU CCPC网络选拔赛 6441 Find Integer（数学）

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/a17865569022/article/details/82053543

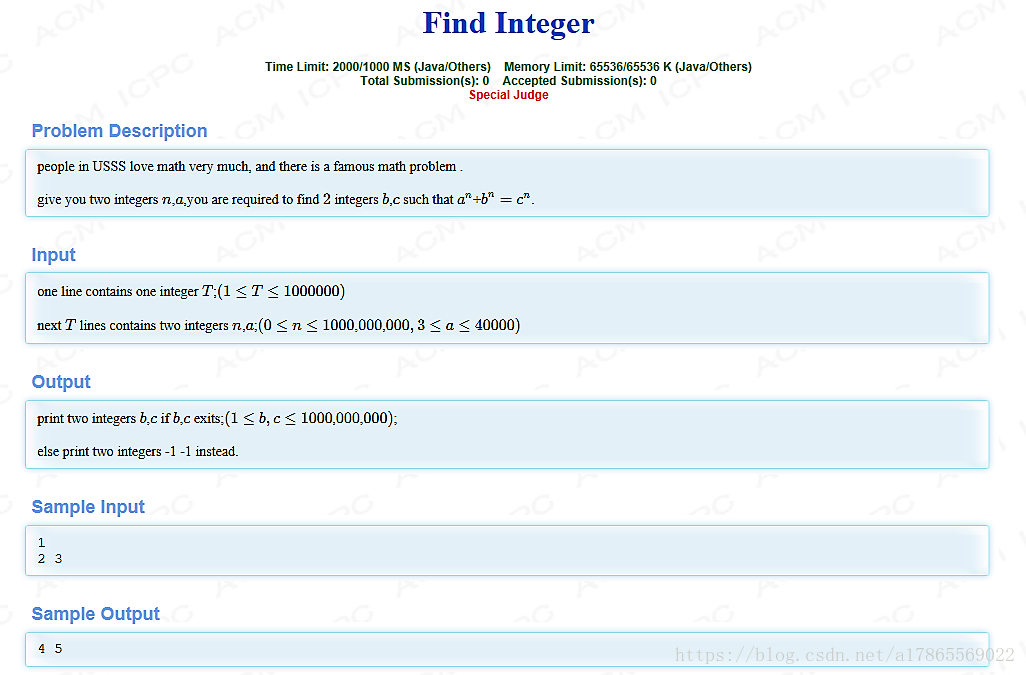
费马大定理只只有n=1或n=2时候才会有解
当n=2时，即满足勾股定理
一， 直角三角形a^2+b^2=c^2的a值奇偶数列法则：
定理1． 如a^2+b^2=c^2是直角三角形的三个整数边长，则必有如下a值的奇数列、偶数列关系成立；
（一） 直角三角形a^2+b^2=c^2奇数列a法则：
若a表为2n+1型奇数（n=1、2、3 …）， 则a为奇数列平方整数解的关系是：
a=2n+1
{ b= n^2+（n+1）^2-1
c= n^2+（n+1）^2
证：由勾股弦定理，若abc为直角三角形三边整数时必有a^2+b^2=c^2关系成立，现将奇数列a法则条件代入勾股弦定理得到下式：
（2n+1）^2+（n^2+（n+1）^2-1）^2=（n^2+（n+1）^2）^2
化简后得到：
4n^4+8n^3+8n^2+4n+1=4n^4+8n^3+8n^2+4n+1
即等式关系成立；
由法则条件分别取n=1、2、3 … 时得到了：
3^2+4^2=5^2
5^2+12^2=13^2
7^2+24^2=25^2
9^2+40^2=41^2
11^2+60^2=61^2
13^2+84^2=85^2
…
故得到奇数列a法则成立
（二） 直角三角形a^2+b^2=c^2的偶数列a法则：
若a表为2n型偶数（n=2、3、4…）， 则a为偶数列平方整数解的关系是：
a= 2n
{ b= n^2 -1
c= n^2+1
证：由勾股弦定理，若abc为直角三角形三边整数时必有a^2+b^2=c^2关系成立，现将偶数列a法则条件代入勾股弦定理得到下式：
（2n）^2+（n^2-1）^2=（n^2+1）^2
化简后得到：
n^4+2n^2+1= n^4+2n^2+1
即等式关系成立；
（这里需要说明，当取n=1时，有b= n2 –1=1-1=0，此时失去三角形意义，故只能取n=2、3、4…）
由法则条件分别取n=2、3、4 … 时得到了：
4^2+3^2=5^2
6^2+8^2=10^2
8^2+15^2=17^2
10^2+24^2=26^2
12^2+35^2=37^2
14^2+48^2=50^2
…
故得到偶数列a关系成立
故定理1关系成立
由定理1得出，当a为≥3的全体整数时， a^2+b^2=c^2的整数解关系都成立。
原链接：直角三角形a^2+b^2=c^2整数解的定a公式直求法

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int main()
{
    int t;cin>>t;
    while(t--)
    {
        LL n,a,b=0,c=0;
        scanf("%lld %lld",&n,&a);
        if(n==1||n==2)
        {
            if(n==1)
            {
                b=1;
                c=a+b;
                printf("%lld %lld\n",b,c);
            }
            else
            {
                if(a%2==1)
                {
                    LL cnt=(a-1)/2;
                    b=cnt*cnt+(cnt+1)*(cnt+1)-1;
                    c=cnt*cnt+(cnt+1)*(cnt+1);
                    printf("%lld %lld\n",b,c);
                }
                else
                {
                    LL cnt=a/2;
                    b=cnt*cnt-1;
                    c=cnt*cnt+1;
                    printf("%lld %lld\n",b,c);
                }
            }
        }
        else printf("-1 -1\n");
    }
    return 0;
}