当你看完这篇朴素贝叶斯（NB）算法后,是否会有怦然心动的感觉

一、引言

当一位气象学家提供天气预报时，通常会使用像"明天70%的可能性会下雨"这样的术语来预测j降雨，这些预测称为下雨的概率。你有没有想过他们是如何计算的呢？

本文将讲述一种机器学习算法，即依靠概率原则进行分类的朴素贝叶斯(Naive Bayes，NB)分类算法。正如气象学家预测天气一样，朴素贝叶斯算法就是应用先前事件的有关数据来估计未来发生的概率，其核心是贝叶斯方法。

本文第2节介绍了贝叶斯方法的基本概念，第3节讲解了《伊索寓言》狼来了故事中的贝叶斯定理，第4节阐述了嫁还是不嫁博弈过程中的朴素贝叶斯方法，第5节作出总结。

二、贝叶斯方法的基本概念

在进入朴素贝叶斯算法学习之前，我们值得花一些时间来定义一些概念，这些概念在贝叶斯方法中经常用到。用一句话概括，贝叶斯概率理论植根于这样一个思想，即一个事件的似然估计应建立在手中已有证据的基础上。

事件

统计学中用“事件”表示有概率可言的任何事情，也就是说，事件是人们能指出发生可能性的任何事情。比如天气为晴天和非晴天，收到垃圾邮件和非垃圾邮件。

如下图

如果A表示收到垃圾邮件，那么 A’被称为A的对立事件，即收到非垃圾邮件。

2. 概率

一个事件发生的概率可以通过观测到的数据来估计，即用该事件发生的试验的次数除以试验的总次数。通常用符号p（A）来表示事件A发生的概率。

例如，如果10天中有3天下雨了，那么就可以估计下雨的概率为30%。同样，如果50封电子邮件中有10封是垃圾邮件，那么可以估计垃圾邮件的概率为20%，即P（垃圾邮件）=0.2。

简而言之：概率值是一个0-1之间的数字，用来衡量一个事件发生可能性的大小。概率值越接近于1，事件发生的可能性越大，概率值越接近于0，事件越不可能发生。

3. 联合概率

联合概率指的是包含多个条件且所有条件同时成立的概率，即如何将一个事件发生的概率和另外一个事件发生的概率联系在一起。对于两个事件A和B，A和B同时发生的概率P（A $\cap$ B）为

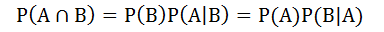
如果这两个事件完全不相关（线性与非线性），我们称为独立事件。例如，抛硬币的结果与天气是晴天还是阴雨天是相互独立的。这时，公式变为

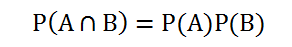
以垃圾邮件事件的的文氏图为例：

如下图，蓝圈代表收到垃圾邮件，红圈代表收到包含词语‘百万美元’的邮件，圆的大小和重叠的程度并不重要，只是用这样一种方法来提醒我们对所有可能的事件组合来分配概率。

那么联合概率的工作就是量化这两个比例之间的重叠程度，换句话说，就是估计P（垃圾邮件）和P（百万美元）同时发生的概率，即P（垃圾邮件 $\cap$ 百万美元）。

4. 基于贝叶斯定理的后验概率

相关事件之间的关系可以用贝叶斯定理来描述，如下面的公式所示

P(B)是B的先验概率，比如我邮箱收到一封邮件，在没有进行浏览的条件下，我根据以往经验（认知）猜这份邮件是垃圾邮件的概率是20%，即为先验概率。

P(A|B) 是已知B发生后A的条件概率，叫做似然概率（likelihood）。比如在先前的垃圾邮件中出现词语百万美元的概率称为似然概率。

P(A)是A的边际概率，又称证据。假设你浏览了电子邮件，发现电子邮件使用了词语百万美元，而百万美元出现在任何一封邮件中的概率称为边际概率。

P(B|A) 为后验概率。这个概率用来衡量在得到证据下，该邮件为垃圾邮件的可能性。

垃圾邮件例子的贝叶斯公式如下

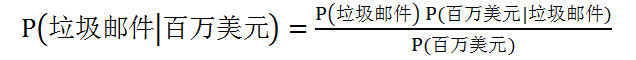
为了计算贝叶斯定理中每一个组成部分的概率，我们必须构造一个频率表（如下面的左图所示），如下图所示

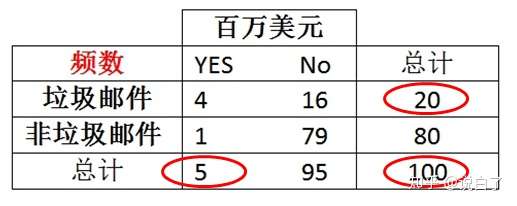
从上表可以得出垃圾邮件的先验概率（频率）为20/100=20%，百万美元的边际概率为5/100=5%。根据该频率表，可以构造似然表，如下图所示。

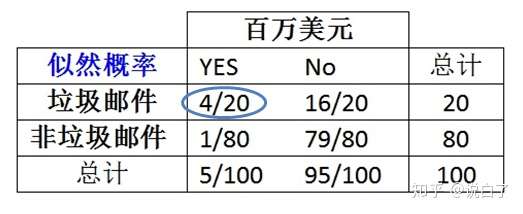
根据似然表，可以得到P（百万美元|垃圾邮件）=4/20=0.20，为了计算后验概率P（垃圾邮件|百万美元），我们利用贝叶斯定理，即

因此，如果电子邮件含有词语百万美元，那么该电子邮件是垃圾邮件的概率为80%。所以，任何含有词语百万美元的消息都需要被过滤掉。这就是商业垃圾邮件过滤器的工作方法，尽管在计算频率表和似然表时会同时考虑更多数目的词语。

在上述的例子中，当我们不知道任何证据的情况下，垃圾邮件的先验概率为20%，而在出现了垃圾邮件使用了词语百万美元的情况下，垃圾邮件的后验概率调整为80%。其实，贝叶斯定理就是通过证据来修正/调整我们对事物的原本认知的，当把贝叶斯公式写成下面的形式时，大家是不是恍然大悟，耳目一新？

三《伊索寓言》狼来了故事中的贝叶斯定理

《伊索寓言》中有一则“孩子与狼”的故事，讲的是一个小孩每天到山上放羊，山里有狼出没。第一天，他在山上喊“狼来了！狼来了！”，山下的村民闻声便去打狼，可到了山上，发现狼没有来；第二天也如此；第三天，狼真的来了，可无论小孩怎么喊叫，也没有人来救他，因为前两天他说了慌，人们不再相信他了。试用贝叶斯公式来分析此寓言中村民对这个小孩的可信度是如何下降的.

这个故事分两个方面，一是小孩，二是村民。小孩有两种行为：一是说谎，二是不说谎；村民有两种行为：一是认为小孩可信，二是认为小孩不可信.

类似的问题都是先设事件:

A:小孩说谎； $\bar{A}$ :小孩没说谎。

B:小孩可信； $\bar{B}$ :小孩不可信。

不妨设过去村民对这个小孩的印象是P（B） = 0.8，P（ $\bar{B}$ ） = 0.2，可见刚开始村民们对这个小孩还是很相信的。用贝叶斯公式计算村民对这个小孩的可信程度的改变时要用到（A|B），P（A| $\bar{B}$ ），即“可信的孩子说谎”的概率与“不可信的孩子说谎”的概率，在此不妨设P（A|B）= 0.1，P（A| $\bar{B}$ ） = 0.5。第一次村民上山打狼，发现狼没有来，即小孩说了谎，村民根据这个信息，将这个小孩的可信程度改变为：

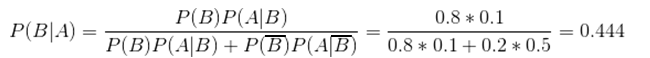
其中，分母就是P(A)的表达式。这表明村民上了一次当后，对这个小孩可信程度由原来的0.8调整为0.444，也就是将村民对这个小孩的最初印象P（B） = 0.8，P（ $\bar{B}$ ） = 0.2调整为P（B） = 0.444，P（ $\bar{B}$ ） = 0.556。

在这个基础上，我们再用贝叶斯公式计算P（B|A），即这个小孩第二次说谎之后，村民认为他的可信程度改变为：

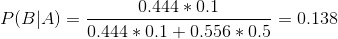
这表明村民经过两次上当后，对这个小孩的信任程度已经由最初的0.8下降到了0.138，如此低的可信度，村民听到第三次呼叫时，怎么再会上山去打狼呢？

这个例子对人来说有很大的启发，即“某人的行为会不断修正其他人对他的看法”。哈哈，有种在算法中感悟人生哲学的赶脚。

四、朴素贝叶斯算法

好的，在这里大家应该已经热身完毕了，那么我们朴素贝叶斯算法的重头戏来了。

我们直接通过一个例子来讲解朴素贝叶斯算法，例子引自带你搞懂朴素贝叶斯分类算法 - CSDN博客，给定数据如下：

现在给我们的问题是，如果一对男女朋友，男生向女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？

这是一个典型的分类问题，转为数学问题就是比较 p(嫁|(不帅、性格不好、身高矮、不上进))与 p(不嫁|(不帅、性格不好、身高矮、不上进))的概率，谁的概率大，我就能给出嫁或者不嫁的答案！

这里我们联系到朴素贝叶斯公式：

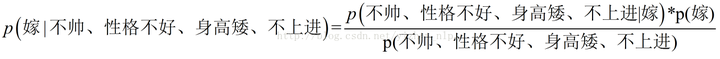
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进)）,这是我们不知道的，但是通过朴素贝叶斯公式可以转化为好求的三个量.

p(不帅、性格不好、身高矮、不上进|嫁)、p（不帅、性格不好、身高矮、不上进)、p(嫁)（至于为什么能求，后面会讲，那么就太好了，将待求的量转化为其它可求的值，这就相当于解决了我们的问题！）

那么这三个量是如何求得？

是根据已知训练数据统计得来，下面详细给出该例子的求解过程。回忆一下我们要求的公式如下：

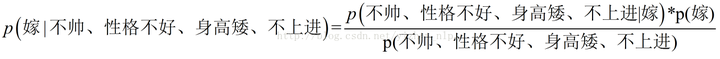
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p（不帅、性格不好、身高矮、不上进)、p(嫁)即可，好的，下面我分别求出这几个概率，最后一比，就得到最终结果。

对的！这也就是为什么朴素贝叶斯分类有朴素一词的来源，朴素贝叶斯算法是假设各个特征之间相互独立，那么这个等式就成立了！但是为什么需要假设特征之间相互独立呢？

1、我们这么想，假如没有这个假设，那么我们对右边这些概率的估计其实是不可做的，这么说，我们这个例子有4个特征，其中帅包括{帅，不帅}，性格包括{不好，好，爆好}，身高包括{高，矮，中}，上进包括{不上进，上进}，那么四个特征的联合概率分布总共是4维空间，总个数为2*3*3*2=36个。多达36个，计算机扫描统计还可以，但是现实生活中，往往有非常多的特征，每一个特征的取值也是非常之多，那么通过统计来估计后面概率的值，变得几乎不可做，这也是为什么需要假设特征之间独立的原因。

2、假如我们没有假设特征之间相互独立，那么我们统计的时候，就需要在整个特征空间中去找，比如统计p(不帅、性格不好、身高矮、不上进|嫁),我们就需要在嫁的条件下，去找四种特征全满足分别是不帅，性格不好，身高矮，不上进的人的个数，这样的话，由于数据的稀疏性，很容易统计到0的情况。这样是不合适的。

根据上面俩个原因，朴素贝叶斯法对条件概率分布做了条件独立性的假设，由于这是一个较强的假设，朴素贝叶斯也由此得名！这一假设使得朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

好的，上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解！我们将上面公式整理一下如下：

下面我将一个一个的进行统计计算（在数据量很大的时候，根据中心极限定理，频率是等于概率的，这里只是一个例子，所以我就进行统计即可）。

p(嫁)=？首先我们整理训练数据中，嫁的样本数如下：

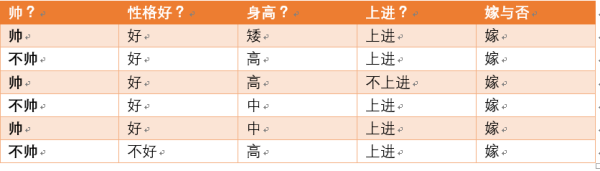
则 p(嫁) = 6/12= 1/2，表示在12个样本中，嫁的人有6个

p(不帅|嫁)=？统计满足样本数如下：

则p(不帅|嫁) = 3/6 = 1/2 ，表示在嫁的条件下，不帅的情况有1/2

p(性格不好|嫁)= ？统计满足样本数如下：

则p(性格不好|嫁)= 1/6

p（矮|嫁） = ? 统计满足样本数如下：

则p(矮|嫁) = 1/6

p(不上进|嫁) = ? 统计满足样本数如下：

则p(不上进|嫁) = 1/6

下面开始求分母，p(不帅)，p（性格不好），p（矮），p（不上进）

统计样本如下：

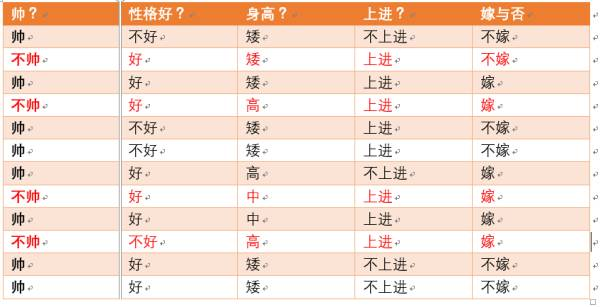
不帅统计如上红色所示，占4个，那么p（不帅） = 4/12 = 1/3

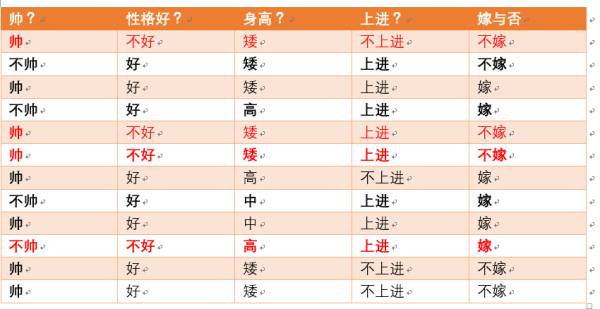
性格不好统计如上红色所示，占4个，那么p（性格不好） = 4/12 = 1/3

身高矮统计如上红色所示，占7个，那么p（身高矮） = 7/12

不上进统计如上红色所示，占4个，那么p（不上进） = 4/12 = 1/3

到这里，要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了，下面我代入进去即可，

= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)

下面我们根据同样的方法来求p(不嫁|不帅，性格不好，身高矮，不上进)，完全一样的做法，为了方便理解，我这里也走一遍帮助理解。首先公式如下：

下面我也一个一个来进行统计计算，这里与上面公式中，分母是一样的，于是我们分母不需要重新统计计算！

p（不嫁）=？根据统计计算如下（红色为满足条件）：

则p(不嫁)=6/12 = 1/2。

p(不帅|不嫁) = ？统计满足条件的样本如下（红色为满足条件）：

则p（不帅|不嫁） = 1/6

p（性格不好|不嫁） = ？据统计计算如下（红色为满足条件）：

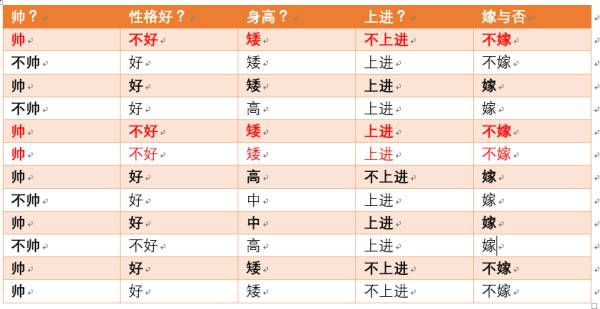
则p（性格不好|不嫁） =3/6 = 1/2

p（矮|不嫁） = ？据统计计算如下（红色为满足条件）：

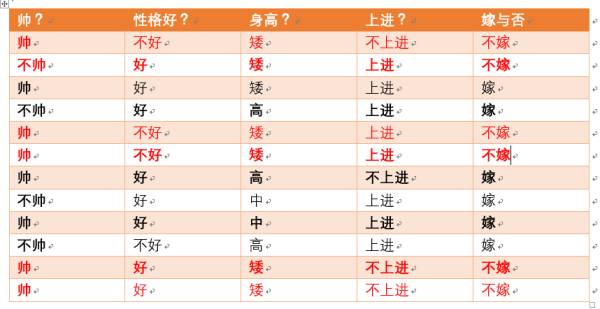
则p（矮|不嫁） = 6/6 = 1

p（不上进|不嫁） = ？据统计计算如下（红色为满足条件）：

则p（不上进|不嫁） = 3/6 = 1/2
那么根据公式：

p (不嫁|不帅、性格不好、身高矮、不上进) = (1/2*1/6*1/2*1*1/2)/(1/3*1/3*7/12*1/3)。

很显然 (1/2*1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)

于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进）。所以我们根据朴素贝叶斯算法可以给这个女生答案，是不嫁！

五总结

朴素贝叶斯算法的主要原理基本已经做了总结，这里对朴素贝叶斯的优缺点做一个总结，详情请参考朴素贝叶斯算法原理小结 - 刘建平Pinard - 博客园。

朴素贝叶斯的主要优点有：

1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练。

朴素贝叶斯的主要缺点有：

1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。2）需要知道先验概率，且先验概率很多时候取决于假设，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。