在之前的一篇博客中L1正则化及其推导推导证明了L1正则化是如何使参数稀疏化人,并且提到过L1正则化如果从贝叶斯的观点看来是Laplace先验,事实上如果从贝叶斯的观点,所有的正则化都是来自于对参数分布的先验。现在来看一下为什么Laplace先验会导出L1正则化,也顺便证明Gauss(高斯)先验会导出L2正则化。
最大似然估计
很多人对最大似然估计不明白,用最简单的线性回归的例子来说:如果有数据集(X,Y)
,并且Y是有白噪声(就是与测量得到的Y与真实的Yreal有均值为零的高斯分布误差),目的是用新产生的X来得到Y
。如果用线性模型来测量,那么有:
f(X)=∑i(xiθi)+ϵ=XθT+ϵ(1.1)
其中X=(x1,x2…xn)
,ϵ是白噪声,即ϵ∼N(0,δ2)。那么于一对数据集(Xi,Yi)来用,在这个模型中用Xi得到Yi的概率是Yi∼N(f(Xi),δ2)
:
P(Yi|Xi,θ)=1δ2π−−√exp(−∥f(Xi)−Yi∥22δ2)(1.2)
假设数据集中每一对数据都是独立的,那么对于数据集来说由X
得到Y
的概率是:
P(Y|X,θ)=∏i1δ2π−−√exp(−∥f(Xi)−Yi∥22δ2)(1.3)
根据决策论,就可以知道可以使概率P(Y|X,θ)
最大的参数θ∗就是最好的参数。那么我们可以直接得到最大似然估计的最直观理解:对于一个模型,调整参数θ,使得用X得到Y的概率最大。那么参数θ
就可以由下式得到:
θ∗=argmaxθ(∏i1ϵ2π−−√exp(−∥f(Xi)−Yi∥22δ2))=argmaxθ(−12δ2∑i∥f(Xi)−Yi∥2+ ∑iln(δ2π−−√))=argminθ(∑i∥f(Xi)−Yi∥2)(1.4)
这个就是最小二乘计算公式。
Laplace分布
Laplace概率密度函数分布为:
f(x|μ,b)=12bexp(−|x−μ|b)(2.1)
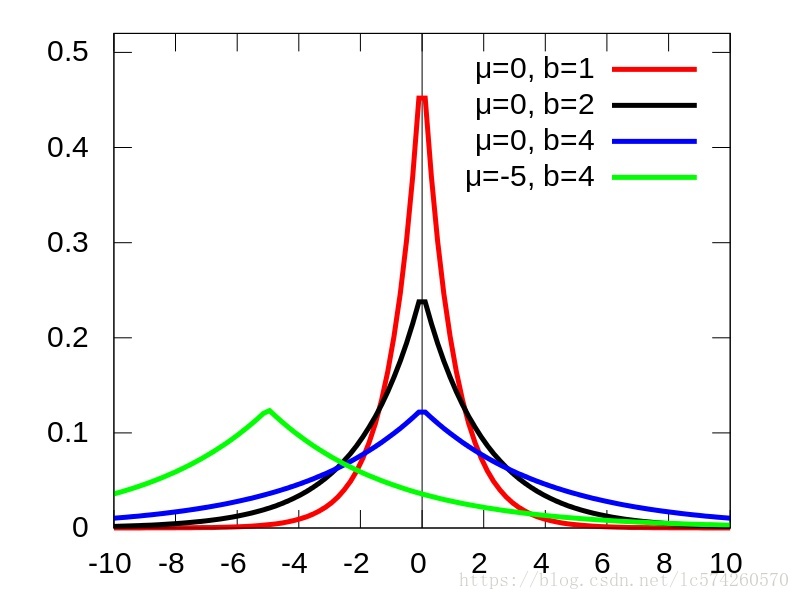
分布的图像如下所示:
图1 Laplace分布
我们能够看出拉普拉斯分布是一个类似正太分布的值
当均值u恒定的时候,我们减小b值(类似正太分布的均值),那么得到的图也就越集中,
之所以laplace分布是一个尖点,是因为绝对值在均值附件就是这样的一种情况,和正太分布还是有差距的。
可以看到Laplace分布集中在μ
附近,而且b
越小,数据的分布就越集中。
Laplace先验导出L1正则化
先验的意思是对一种未知的东西的假设,比如说我们看到一个正方体的骰子,那么我们会假设他的各个面朝上的概率都是1/6
,这个就是先验。但事实上骰子的材质可能是密度不均的,所以还要从数据集中学习到更接近现实情况的概率。同样,在机器学习中,我们会根据一些已知的知识对参数的分布进行一定的假设,这个就是先验。有先验的好处就是可以在较小的数据集中有良好的泛化性能,当然这是在先验分布是接近真实分布的情况下得到的了,从信息论的角度看,向系统加入了正确先验这个信息,肯定会提高系统的性能。我们假设参数θ
是如下的Laplace分布的,这就是Laplace先验:
P(θi)=λ2exp(−λ|θi|)(3.1)
其中λ
是控制参数θ集中情况的超参数,λ
越大那么参数的分布就越集中在0附近。
在前面所说的最大似然估计事实上是假设了θ
是均匀分布的,也就是P(θ)=Constant
,我们最大化的要后验估计,即是:
θ∗=argmaxθ(∏iP(Yi|Xi,θ)∏iP(θi))=argminθ(∑i∥f(Xi)−Yi∥2+∑iln(P(θi)))(3.2)
如果是Laplace先验,将式(3.1)
代入到式(3.2)
中可得:
θ∗=argminθ(∑i∥f(Xi)−Yi∥2+λ∑i|θi|))(3.3)
这就是由Laplace导出L1正则化,我在之前的一篇博客中L1正则化及其推导分析过λ
越大,那么参数的分布就越集中在0附近,这个与Laplace先验的分析是一致的。
Gauss先验导出L2正则化
到这里,我们可以很轻易地导出L2正则化,假设参数θ
的分布是符合以下的高斯分布:
P(θi)=λπ−−√exp(−λ∥θi∥2)(3.4)
代入式(3.2)
可以直接得到L2正则化:
θ∗=argminθ(∑i∥f(Xi)−Yi∥2+λ∑i∥θi∥2))(3.5)
公式不想编辑,这是原文的转载连接
https://www.cnblogs.com/heguanyou/p/7688344.html