Opencv之拉普拉斯Laplace算子及其边缘检测

学习资料参考：

张平.《OpenCV算法精解：基于Python与C++》.[Z].北京.电子工业出版社.2017.

---

前言

简述一下什么是Laplace运算。
拉普拉斯从定义上讲是梯度的散度。符号表示为$△f=▽.▽f$（其中$▽$是梯度符号，$▽.$是散度的符号）
对于函数$f(x,y,z)$,它的梯度表示为$▽f=\frac{\partial f}{\partial x}\ast i+\frac{\partial f}{\partial y}\ast j+\frac{\partial f}{\partial z}\ast k$.
对应的该梯度的散度表示为$△f=▽.▽f=(\frac{\partial }{\partial x}\ast i+\frac{\partial }{\partial y}\ast j+\frac{\partial }{\partial z}\ast k).(\frac{\partial f}{\partial x}\ast i+\frac{\partial f}{\partial y}\ast j+\frac{\partial f}{\partial z}\ast k)=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}+\frac{{\partial }^{2}f}{\partial z^2}$.

那么将Laplace算子运用于图像的表示时，采用差分近似微分的方法。而该方法包含向前差分与向后差分。
若图像$I$，对于图像对应的二维矩阵某一点的像数值设为$I(x,y)$,那么该点的差分表示为
$▽f_x^{F}I(x,y)=I(x+1,y)-I(x,y)，▽f_x^{B}I(x,y)=I(x,y)-I(x-1,y)$
那么在$(x,y)$处的Laplace运算结果为${△}_{x}I(x,y)={▽}_x^F({▽}_x^B(x,y))={▽}_x^F(I(x,y)-I(x-1,y))={▽}_x^F(I(x,y))-{▽}_x^F(I(x-1,y))=I(x+1,y)-I(x,y)-(I(x,y)-I(x-1,y))=I(x+1,y)+I(x-1,y)-2I(x,y)$

上面的式子推算满足某些计算规则，不想看。请看下面，不那么严谨的理解。

---

不那么严谨的理解拉普拉斯算子

拉普拉斯算子与多元变量函数的二阶导类似。如果拉普拉斯取正的最大值，那么说明该点是最小值所在的位置；如果拉普拉斯取负的最大值，那么说明该点是最大值所在的位置。截取biliili上某视频讲解的图片：

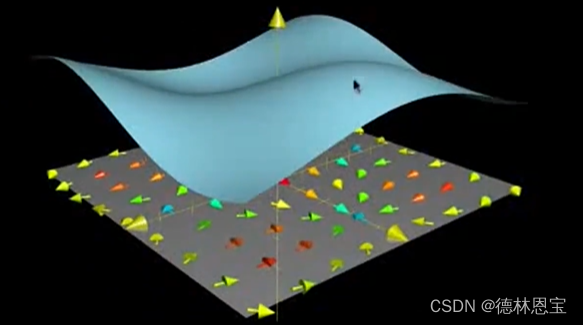
上图中，凹下去的部分就是拉普拉斯取正最大值的位置，凸出来的部分就是拉普来说取负最大值的位置。
散度为正，表示该点是发散状态，就像只会往外喷发的火山；散度为负，表示该点是收拢状态，就像只会收纳万物的黑洞。
而梯度表示函数值上升的最大最快的方向，那么对梯度求散度。散度为正值，表明该处的梯度是往外走的，也就是该处是最低点，符合梯度的定义；散度为负值，表明该处的梯度是往内走的，也就是该处是最高点，也符合梯度的定义。

---

原理

经过前文的介绍，下面的式子也就好理解了。

根据上述的表达式可得到一下卷积核：

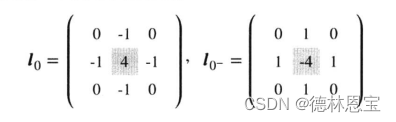
从该卷积核分析可知，对噪声比较敏感。对于为什么敏感呢？
设定在图片中的一个很暗的区域，其中出现了一个很亮的点，即该点的像素值较周围的其他像素的值大很多，那么我们知道拉普拉斯对于求解最大值和最小值的过度区间存在零值，那么根据这个零值就可以区分边缘。因此对孤立点更加敏感，噪声就是这种孤立点。
那么拉普拉斯就尤其适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。

那如何将拉普拉斯算子与图像的边缘联系起来？
我们知道如果将拉普拉斯的卷积核与图像进行卷积之后，就会得到每一个像素点的梯度的散度。该散度有正值，也有负值。结合前面不那么严谨的理解可知，正值与负值之间存在0这个状态，那么该零值就被作为边缘的分界点，当然想说不对，也想不出不对的道理，试试看，进行图像的阈值化。

其次，拉普拉斯核内所有值的和必须等于0，这样就是的在恒等灰度值区域不会产生错误的边缘，并且该核是不可分离的。

那为什么不为0就要产生错误的边缘呢？
因为不为0的话，很明显的一个点就是导致权值不等，使用不为0的进行试验后，很大可能发现像素的差异。

---

python实现

import numpy as np
from scipy import signal
import cv2


def laplacian(image, _boundary="fill", _fillvalue=0):
    laplacianKernel = np.array([[0, -1, 0], [-1, 4, -1],
                                [0, -1, 0]],np.float32)
    # 图像与拉普拉斯进行卷积
    i_conv_lap = signal.convolve2d(image, laplacianKernel, mode='same',boundary=_boundary,fillvalue=_fillvalue)
    return i_conv_lap


if __name__=="__main__":
    image = cv2.imread(r"C:\Users\1\Pictures\test1.jpg", 0)
    i_conv_lap = laplacian(image, 'symm')
    # 对卷积结果进行阈值化处理
    threshEdge = np.copy(i_conv_lap)
    threshEdge[threshEdge > 0] = 255
    threshEdge[threshEdge <= 0] = 0
    threshEdge = threshEdge.astype(np.uint8)
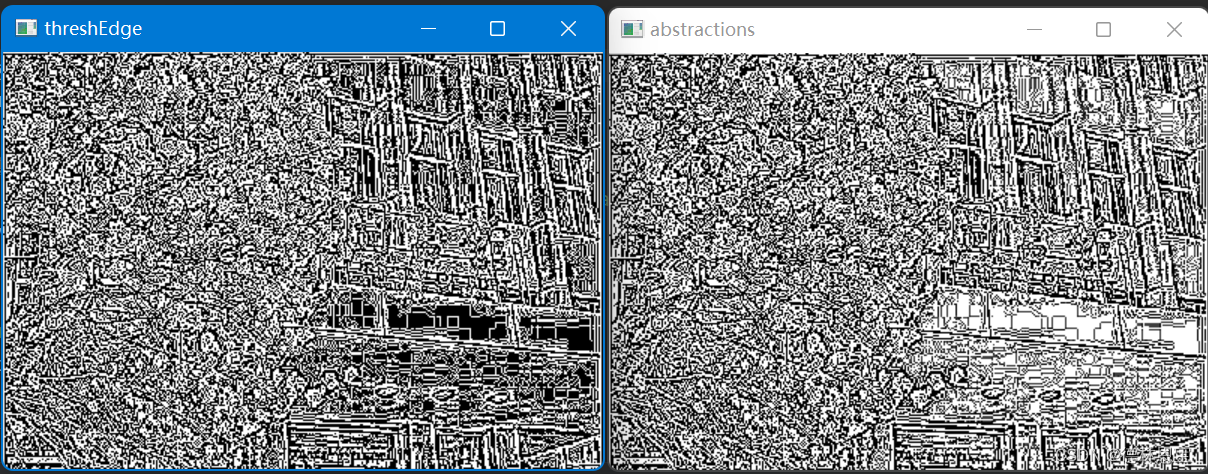
    cv2.imshow("threshEdge", threshEdge)
    # 对卷积结构进行抽象化处理
    abstractions = np.copy(i_conv_lap)
    abstractions = abstractions.astype(np.float32)
    abstractions[abstractions >= 0] = 1.0
    abstractions[abstractions < 0] = 1.0 + np.tanh(abstractions[abstractions < 0])
    cv2.imshow("abstractions", abstractions)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

运行结果