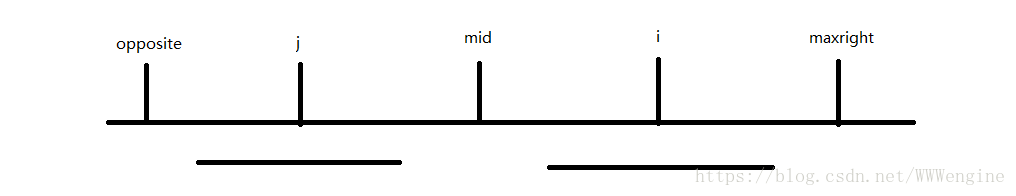例题见洛谷P3805：洛谷P3805
一个大神的博客：http://www.cnblogs.com/grandyang/p/4475985.html
暴力
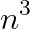：枚举每一个子串，然后判断是不是回文的。
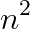：枚举每个点，以该点向左右同时扩展。
Manacher
>>首先搬一下这个算法的原理，主要是利用了回文子串中，左右部分划分出的子串仍有对称性的特点，尤其是利用了长度相等。
>>以下定义记住就行：
1，若原串为s，设p[i]表示算上s[i]时，以s[i]为中心扩展的回文串最大半径。例如：aaacaaa，c对应的p[i]就是4。
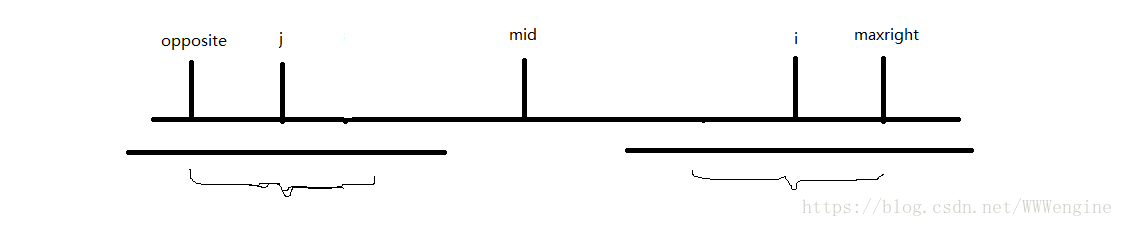
2，设maxright为字符串向右到达过的最远的下标，mid表示最长回文子串的对称点，i则是当前枚举到的字符下标。可以想到，mid和maxright是同时更新的。为了帮助理解，设一个opposite，表示maxright关于mid的对称点；设一个j，表示i关于mid的对称点，可以算得j=mid*2-i。
>>然后开始分析：
1，回文串长度有奇偶，解决方法是在两个字符之间插入一个原串没有的字符，比如：
aaacaaa - #a#a#a#c#a#a#a# 。
如此一来所有的回文串长度都是奇数。在首尾插入是为了方便操作。可以发现，p[i]-1就是以i为中心的最长回文子串长度（去掉#）。
2，求p[i]的式子为：
这是该算法的核心所在，下面将画图理解
**情况1： maxright > i，则以s[i]为对称中心的最大回文串半径一定包括在或者相交于mid~maxright这一段。又分两种情况。
这种情况下，以j和以i为对称点的最长回文子串完全包括在里面，因为mid两边对称的关系，所以p[i]=p[j]=p[mid*2-i]。
这种情况下，并未完全包含，但至少可以保证i~maxright这一段是可取的。于是取到maxright-i。如果还有一段，就直接向两边拓展直到不匹配为止。
**情况2：i超过了maxright，那么直接赋初值为1，表示自己本身是一个回文子串。
3，其它变量的更新。上面的式子解决后其它的便不成问题。
首先通过上面的式子初步得到的p[i]还可能继续拓展，所以一个while来继续更新，得到最后的p[i]。然后可以比较maxright和p[i]+i-1来更新maxright和mid；同时更新答案。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int MAXN=11000005;
int p[MAXN*2],N=0;
char s[MAXN*2],c[MAXN];
void solve()
{
scanf("%s",c);
int len=strlen(c),i=0;
s[N]='$';s[++N]='#';
while(i<len)
{
s[++N]=c[i];
s[++N]='#';
i++;
} s[N+1]='\0'; //插入其他字符
int mid=0,maxright=0,ans=0;
for(int i=1;i<=N;i++)
{
p[i]=i>maxright?1:min(p[mid*2-i],maxright-i);
while(s[i+p[i]]==s[i-p[i]]) p[i]++; //向左右拓展
if(p[i]+i-1>maxright)
{
maxright=p[i]+i-1;
mid=i;
}
ans=max(ans,p[i]-1);
}
cout<<ans;
}
int main()
{
solve();
return 0;
}